Глава V. Элементы квантовой механики

§ 5.1. Волны де Бройля

В 1923 г. молодой французский физик Луи де Бройль, исходя из соображений симметрии, предположил, что корпускулярно-волновой дуализм являет собой универсальный закон природы, которому подчиняются на только фотоны, но и все частицы, имеющие массу покоя, например, электроны. Свободная частица, движущаяся равномерно и прямолинейно с импульсом p=mυ, представляет собой гармоническую волну, длина которой определяется той же формулой (4.12), что и для фотона:

λ= (5.1)

В те времена казалось, что волновые свойства частиц – не более, чем игра ума. Однако спустя три года волна де Бройля получила экспериментальное подтверждение. Американские исследователи Дэвисон и Джермер случайно обнаружили, направив на монокристалл никеля пучок электронов с одинаковой энергией, что результаты рассеяния очень напоминают дифракционную картину: интенсивность рассеянного пучка зависела от угла рассеяния не монотонно, а имела четко выраженные максимумы и минимумы. Подобную картину давала дифракция рентгеновских лучей на монокристалле никеля, кристаллическая решетка которого играла роль дифракционной решетки. Электроны, прошедшие ускоряющую разность потенциалов U, приобретают кинетическую энергию mυ ²/2= eU. Их длина волны в соответствии с формулой (4.13) λ = h/ = 1,225/ нм. Для электронов, прошедших ускоряющую разность потенциалов U= 100 В, λ= 1,225^.10^-10 м = 1,225 [2], что соответствует рентгеновскому диапазону.

на станции метро или пригородных электропоездов.

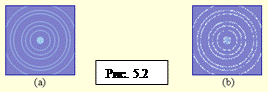
Независимо от этих опытов в том же году Томсон наблюдал дифракционную картину, пропуская электронный пучок через тонкую поликристаллическую металлическую фольгу. Схема его установки представлена на рис. 5.1 Катод К и анод А формируют узкий пучок электронов, который проходит через фольгу Ф и попадает на фотопластинку. Полученное на ней изображение представлено на рис. 5.2. Рассеянные фольгой электроны летят только в определенных направлениях. Их точечные следы на фотопластинке группируются в кольца. На рис 5.2.(а) плотность электронных следов так велика, что точки сливаются в линии. На рис. 5.2 (б) заметны точечные следы отдельных электронов, так как их число еще не столь велико, как в случае (а). Эти кольца – типичная картина максимумов и минимумов интенсивности при дифракции рентгеновских лучей на этой же фольге, если их длина волны совпадает с длиной волны де Бройля для электронов. Таким образом, этот опыт явно продемонстрировал волновую природу электрона. Впоследствии опыты подтвердили, что волновыми свойствами обладают не только электроны, но и другие частицы, например, нейтроны. Электронные волны используются в электронных микроскопах, чья разрешающая способность в сотни и тысячи раз превосходит световые микроскопы.

Заметим, что волновым проявлением является дифракция. Она становится заметной при взаимодействии волны с препятствиями, размеры которых не сильно велики по сравнению с длиной волны. Самыми «мелкими» дифракционными решетками являются кристаллические решетки твердых тел, их постоянная составляет величину порядка размеров атома (несколько ангстрем). Для массивных частиц, например, дробинки массой 1 г, летящей со скоростью 100 м/с, длина волны де Бройля составляет порядка 10^-33 м (этот результат получите самостоятельно), так что наблюдать ее волновые свойства невозможно. Физические объекты, проявляющие свойства как волны, так и частицы, называют микрочастицами. К ним относятся фотоны, электроны и другие объекты микромира.

§ 5.2. Соотношения неопределенностей Гейзенберга

Всякая теория использует для описания поведения реальных объектов окружающего мира абстрактные модели, которые учитывают наиболее существенные свойства этих объектов в конкретной ситуации. Классическая физика работает с макротелами и использует две разных модели: точечный объект – частица или бесконечно протяженный объект – гармоническая волна. Каждый физический объект классической физики является либо волной, либо частицей.

Иначе обстоит дело в микромире. Микрочастицы умеют вести себя то как волны, то как частицы, т.е. проявляют корпускулярно-волновой дуализм. Это означает, что они не являются ни классическими частицами, ни классическими волнами, и эти обе модели могут быть применены к ним с определенными ограничениями.

Эти ограничения отражены в соотношениях неопределенностей Гейзенберга (1927 г.). Существуют пары величин, неопределенности (ошибки измерений) которых взаимосвязаны друг с другом. Такие величины называются сопряженными. Чем точнее определена одна из этих величин, тем менее точно может быть определена другая. Такими величинами являются координата микрочастицы (например, х) и проекция ее импульса на эту ось координат (р_х). Произведение их неопределенностей не может быть меньше постоянной Планка h:

∆ x ∆ р_х≥ h (5.2)

Подобное соотношение неопределенностей выполняется для любых осей координат, в том числе и для осей у и z, тогда как произведение ∆ y ∆ р_х может иметь любое значения, в том числе и нулевое. Автомобиль не проваливается сквозь дорогу, потому что он пытается «смять» электронные оболочки атомов, приблизить электроны к ядру и уменьшить ∆ x. Это приводит к увеличению ∆ р_х и возрастанию сопротивления смятию. Соотношение неопределенностей математически выражает корпускулярно-волновой дуализм микрочастиц. Действительно, с точки зрения классической модели координату частицы можно измерить точно, остановив частицу, так что ∆ x =0. Но тогда неизвестной становится ее скорость (импульс) до остановки, так что ∆ р_х= ¥. Частота классической гармонической волны неизменна, а сама волна занимает бесконечно протяженную область пространства. Гармоническая волна де Бройля соответствует частице с неизменным импульсом (см. формулу 5.2). Для такого объекта ∆ x= ¥, ∆ р_х =0. Классическое понятие траектории теряет смысл для микрочастиц. Действительно, состояние классической частицы задают ее координата и импульс (рис. 5.3). Неопределенность координаты и импульса «размывает» траекторию, так что микрочастица скорее похожа на волновое облако, нежели на точку.

Существует еще пара сопряженных величин: энергия и время:

∆ Е ∆ t≥ h (5.3)

Здесь ∆ Е – неопределенность энергии,∆ t – неопределенность времени, она равна промежутку времени, необходимому для измерения значения энергии Е, или времени нахождения микрочастицы в состоянии с энергией Е. Наблюдаемая на опыте естественная ширина спектральных линий также объясняется соотношением неопределенностей (5.3).

Соотношения неопределенностей – один из важнейших законов физики. В природе не существует таких физических объектов, для которых произведение неопределенностей сопряженных величин было бы меньше постоянной Планка. Для реальных физических объектов наименьшее значение произведения неопределенностей сопряженных величин всегда чуть больше или даже много больше значения постоянной Планка. Если в рассматриваемом случае произведение неопределенностей сопряженных величин столь велико по сравнению с постоянной Планка, так что можно считать h »0, то здесь применимы формулы законов классической механики, т.е. законы Ньютона. Если же численным значением h нельзя пренебречь по сравнению с произведением неопределенностей сопряженных величин, то это квантовый объект, к нему надо применять формулы законов квантовой механики. Таким образом, соотношение неопределенностей служит границей между классическими и квантовыми частицами: ∆ x ∆ р_х >> h – классическая частица, ∆ x ∆ р_х≥ h – квантовая частица, ∆ x ∆ р_х < h – такую частицу невозможно наблюдать в опыте.

§ 5.3. Волновая функция. Уравнение Шредингера

Корпускулярно волновой дуализм отрицает возможность задать состояние микрочастицы указанием ее координат и импульса, как для классической частицы. М. Борн в 1926 г. использовал то же самое вероятностное толкование связи волновых и корпускулярных свойств микрочастиц, что и для фотонов: вероятностью их появления в данной точке пространства управляет волна. Еще раз обратимся к рис. 5.2 (б): точечные следы электронов на фотопластинке образуют дифракционные кольца – частиц много в области максимума интенсивности волнового поля, и совсем нет там, где его интенсивность равна нулю.

Это волна вероятности, ее описывают волновой функцией, которую обозначают Y и называют также пси-функцией. В общем случае волновая функция является комплексной функцией координат и времени и не сопоставима с какой-либо физической величиной, измеряемой в опыте, т.е. не имеет физического смысла. Физический смысл имеет квадрат модуля волновой функции |Y| ². Он равен плотности вероятности попадания микрочастицы в малый объем пространства вблизи данной точки:

∆p= |Y| ² ∆V (5.4)

Здесь ∆p -вероятность, измеряемая отношением числа частиц ∆N, попавших в малый объем ∆V вблизи точки пространства, в которой известна волновая функция Y, ко всему числу частиц N, участвующих в опыте. Таким образом, ∆N ~ |Y| ².

Математическая функция, выражающая вероятность, является конечной, однозначной и непрерывной. Такому же условию конечности, однозначности и непрерывности (КОН) отвечает Y-функция. Вероятность обнаружить рассматриваемую микрочастица в области пространства, где она существует, равна единице, следовательно,

=1 (5.5)

Формула (5.5) математически обозначает, что Y-функция нормирована на единицу.

Для определения закона движения конкретного физического объекта необходимо составить и решить уравнение движения. Для классической частицы таковым является второй закон Ньютона, для микрочастицы – уравнение Шредингера. Оба эти уравнения не выводятся из других физических законов, а постулируются. Их действенность проверяется опытом. Закон движения зависит от внешнего воздействия. Мерой внешнего воздействия для классической частицы является сила. Для микрочастицы классическое понятие силы, как и понятие траектории не имеет смысла. Воздействие на микрочастицу характеризуется потенциальной энергией U. Ее математическая формула называется потенциальной функцией и в общем случае является функцией координат и времени. Для простейшего случая одномерного стационарного (не изменяющегося со временем) движения микрочастицы волновая и потенциальная функции зависят только от одной координаты: U = U (х), Y= y (х), и уравнение Шредингера имеет вид:

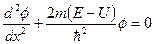(5.6)

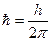, ее называют «аш перечеркнутое» или «аш с чертой», она имеет смысл постоянной Планка (Е _ф= hν= ), Е – полная энергия микрочастицы. Зная потенциальную функцию U = U (х), и решив уравнение (5.6), получают закон движения микрочастицы в виде математической формулы y - функции, квадрат модуля которой с определенной вероятностью указывает положение частицы.

Уравнение Шредингера – это основное уравнение квантовой (или волновой) механики.

§ 5.4. Примеры решения уравнения Шредингера

Пример 1. Свободная частица. Для нее U= 0, и уравнение Шредингера имеет вид, знакомый нам по гармоническому осциллятору: . Его решение - гармоническая функция y = Аsin (kx+φ₀), где А и φ₀ – постоянные, k = . Учитывая, что 2 mE=p², получаем: k= , где λ – длина волны де Бройля (см. формулу 5.1). Таким образом, из уравнения Шредингера следует, что свободная частица – та самая гармоническая волна де Бройля.

Пример 2. Частица в бесконечно глубокой потенциальной яме (БГПЯ).

Потенциальной ямой называется область пространства, где потенциальная энергия достигает минимума. БГПЯ представляет собой бесконечно глубокий колодец с отвесными стенками:

U= ¥ для х <0

U= 0 для х ≤0≤ а

U= ¥ для х >0

Понятно, что частица может находиться только внутри ямы в области х ≤0≤ а, где уравнение Шредингера и волновая функция соответствуют свободной частице. Мы рассмотрели ее в примере 1 и получили y(х) = Аsin (kx+φ₀). За стенками ямы y= 0. В соответствии с условиями КОН волновой функции y(0) = Аsinφ₀, откуда следует, что φ₀ =0, и y(а) = Аsinkа= 0, а это возможно, когда kа=πn, где n= 1,2,3…- любое целое число (n= 0 мы использовали на левой границе ямы). Решение уравнения Шредингера дает, что частице в БГПЯ соответствует множество состояний y_n (n =1,2,…, ¥) с волновыми функциями y_n(х) = Аsin (), являющимися стоячими волнами де Бройля с длинами волн λ_n= 2 a/n, когда на ширине ямы укладывается целое число половин длин волн. Учитывая, что k = , получаем, что каждому состоянию частицы соответствует своя энергия E_n= . Удовлетворяющие уравнению Шредингера волновые функции и соответствующие им энергии частицы называются собственными функциями и собственными значениями энергии. Совокупность собственных значений энергии образует дискретный ряд. Это значит, что энергия частицы может изменяться не плавно, а ступенчато, т.е. энергия квантуется. Разрешенные значения энергии называют уровнями энергии, номер уровня n называют квантовым числом. Энергия низшего уровня E₁= , энергия всех остальных уровней больше наименьшей в n² раз: E_n=E₁n². На рис 5.4 показаны уровни энергии и соответствующие этим состояниям частицы их волновые функции. Найдем различие между соседними уровнями энергии: ∆E=E_n+1 – E_n » n,для n не слишком малых. Пусть электрон находится в потенциальной яме размера атома: а =10^-10 м. Для него ∆E» Дж »50 n эВ. Это вполне заметное в опыте квантование энергии. Для маленькой пылинки массой 10 мг в области размером 1 мм ∆E оказывается меньше на 28 порядков, т.е. различие между соседними уровнями энергии столь мало, что квантование энергии обнаружить невозможно, так что энергия пылинки, как и всякой классической частицы, может изменяться непрерывно, а не ступенчато. Из рис. 5.4 видно, что плотность вероятности | y | ² по-разному распределена по ширине потенциальной ямы для частиц с разными энергиями. Так, для n =1 «капкан» для частицы следует установить посередине ямы, тогда как частицу в состоянии n= 2 в этом месте ожидать бесполезно. Энергия классической частицы (макрочастицы) соответствует очень большим значениям квантового числа n. Ее волновая функция представляет собой стоячую волну со столь малой длиной волны, что ее узлы и пучности практически сливаются, и плотность вероятности одинакова по всей ширине ямы. Квантовый результат соответствует классическому: частица равномерно движется на любой высоте от одной стенки до другой, изменяя направление скорости на противоположное при упругом столкновении со стенкой. Рассмотренный пример показывает, что уравнение движения квантовой механики органично содержит в себе идеи корпускулярно-волнового дуализма и квантования, и применимо как к микро-, так и макрочастицам.

Пример 3. Туннельный эффект представляет собой проникновение микрочастицы сквозь потенциальный барьер. Потенциальным барьером называется область пространства, где потенциальная энергия U больше полной энергии E. Согласно классической механике, частица не может оказаться внутри барьера, так как там ее кинетическая энергия должна быть отрицательной, что невозможно по определению. Налетая на барьер, такая частица должна отразиться от него, и проникнуть за барьер она может лишь в том случае, если в барьере есть туннель. Вспомните железнодорожные туннели, например, в Уральских горах.

Простейший прямоугольный потенциальный барьер представлен на рис. 5.5.

U= 0 в области 1, где х <0;

U=U₀ в области 2, где 0≤ х ≤ a;

U= 0 в области 3, где х > а.

Решение уравнения Шредингера дает отличные от нуля волновые функции y ₁, y ₂ и y ₃во всех трех областях: до барьера, внутри него и за барьером. y ₁ и y ₃ – гармонические функции, y ₂ экспоненциально уменьшается с ростом х от 0 до а. Амплитуда волновой функции в области 3 меньше ее амплитуды в области 1, а значит, число частиц N ₃~| y ₃| ², прошедших сквозь барьер, меньше числа частиц N ₁~| y ₁| ², падающих на барьер.

Прозрачность барьера D характеризует вероятность прохождения частицы сквозь барьер: D= N ₃/ N ₁~ ехр . Заметим, что показатель экспоненты может быть преобразован так: = , где λ- длина волны де Бройля. Если ширина барьера значительно превосходит длину волны де Бройля, то прозрачность барьера практически равна нулю. Туннельный эффект – сугубо квантовое явление, наблюдающееся в микромире. Примером туннельного эффекта является α-распад радиоактивных ядер. Теория туннельного эффекта дает хорошее согласие с измеряемым в опыте периодом полураспада.

§ 5.5. Итоги главы 5

Физический мир имеет двойственную корпускулярно-волновую природу и подчиняется законам квантовой механики. Для объектов и явлений макромира численное значение комбинации характерных для них величин, имеющих размерность постоянной Планка (например, момент импульса mυr) очень велико по сравнению с h. Тогда при вычислениях можно принять h =0, и «более правильная» квантовая теория дает те же результаты, что и классическая. Точнее сказать, что классическая механика является частным случаем механики квантовой. Классическая механика может применяться только для описания макроскопических явлений, тогда как квантовая механика правильно описывает как явления макромира, так и явления микромира, т.е. мира атомов и атомных структур. Формулы классической механики и ее математический аппарат заметно проще механики квантовой, и для большинства инженерных задач не потеряли свою актуальность, несмотря на их ограниченную область применения.

[1] Самостоятельно убедитесь в этом, используя рассмотренные выше определения.

[2] - так обозначают единицу измерения длины, она называется ангстрем; 1 = 10^-10м