Cvoistva
1 Это вероятность достоверного события If m = n then p = 1 p(A) = m/n = 1
2 Это вероятность невозможного события if m = 0 its fals
3 Это вероятность случайного события 0 <m<n so 0<m/n<1
3 Теоремы сложения вероятностей.
Теорема1. Вероятность появления одного из двух несовместных событий, безразлично какого, равно сумме вероятностей этих событий:
P(A+B)=P(A)+P(B)
Теорема2. Сумма вероятностей событий A1, А2, …Аn, образующих полную группу, равна единице:
P(A1)+ P(A2)+….. P(An)= 1
Теорема3. Сумма вероятностей противоположных событий
P(A)+P(A {fo2 al a fy sh76a})= 1
Теорема умножения вероятностей.
Т1. Двух событий P(AB)=P(A)P otA(B)
Т2. Двух независимых событий P(AB)=P(A)P (B)
Формула полной вероятности.
P(A) =P(B1) Pb1(A)+ P(B2)Pb2(A)...+P(Bn)Pbn(A)
6. Формула Бейеса.
PA(B1)= P(B1)Pb1(A)------------------------
P(B1) Pb1(A) +P(B2)Pb2(A)
7 Повторение испытаний. Частная теорема о повторении опыта
Формула Бернулли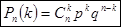 
Локальная теорема Лапласа Y= 1/(npq)_-1*ф(x)
= Y = 1/(npq)_1*1/(2 * 3.14)_1* e_(-x*x)/2
8. Общая теорема о повторении опытов. Производящая функция
Если производятся n независимых опытов в различных условиях, причем вероятность появления события А в i-м опыте равна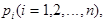 
то вероятность Р 
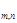того, что событие А в n опытах появится m раз, равна коэффициенту при Z 
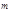в разложении по степеням Z производящей функции 
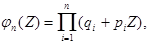где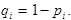 
9. Функция распределения случайной величины.
F(x)=P(X<x).
Свойство1. 0≤F(x) ≤1
Свойство2. F(x2)≥ F(x1), если х2>x1.
Следствие1. P(a≤X<b)=F(b)-F(a).
Следствие2.P(x1≤X<x2+deltax)=F(x1+deltax)-F(x1)
10. Плотность распределения.
F(x)=F ’ (x)
Tearema P(a<x<b) = 
Числовые характеристики случайных величин.
Mat ag M(x)=x1p1+x2P2+,,,, xnpn
Cvoisva
1 M(C)= c
2 m(cx)=cm(x)
3 m(xy)= m(x)m(y)
Неравенство Чебышева.
P(I x-M(x)I<e)>=1-D(x)/e^2
Теорема Чебышева
Ix1+x2+…xn/n)(M(x1)+ M(x2)+… M(xn)/nI<Ƹ
Обобщенная теорема Чебышева и теорема Маркова
Характеристические функции
Центральная предельная теорема.
Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.
Следствие из теоремы Ляпунова-теоремы Лапласа.
Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.
Локальная Теорема Лапласа: если вероятность р появления события А в каждом испытании постоянна и отлична от еуля и единицы, то вероятность Рn(к) того, что событие А появится в n испытаниях равно к раз, приближенно равна (тем меньше, чем больше n) значению функции Y= 1/(npq)_-1*ф(x)
Интегральная теорема Лапласа: Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Pn(K1, K2) того, что событие А появляется в n испытаниях от к1 до к2 раз, приближенно равна определенному интегралу Pn (K1,K2) = 1 / (2*3,14)^1/2
Свойства числовых характеристик(мат ожидание, дисперсия).
Mat ag M(x)=x1p1+x2P2+,,,, xnpn
Cvoisva
1 M(C)= c
2 m(cx)=cm(x)
3 m(xy)= m(x)m(y)
Дис
D(x)= M (x^2) – {M(x)}^2
Or+ D(x)=M{x-M(x)}^2
Svoistva
1 D(c)=0
2 D(cx)=c^2D(x)
3 D(x+y)= D(x) + D(y)
4 D(x-y)= D(x) + D(y)
19 Нормальное распределение
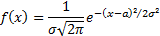
Правило «трех сигма
P x a 3sigma 2 Ф
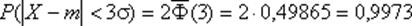
Равномерное распределение
На практике очень часто встречаются случ числа, про которые заранее известно, чтоих значения лежат в пределах некоторого интервала, и все значения случ величины одинаково вероятны.
О таких случ числах говорят, что они распределены равномерно. Плотность такого распределения сохраняет постоянное значение, а именно f(x)=1/(b-a). Вне этого интервала f(x)=0.
Вероятность попадания значения случ числа в заданный интервал (a;b), можно вычислить по формуле: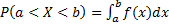 
.
График плотности равомерного распределения симметричен относительно прямой x=(a+b)/2, поэтому M(x)=(a+b)/2. Этот же результат можно получить по формуле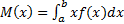 
.
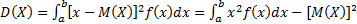. Подставив формулы, полученные выше, получим D(x)=(b-a)²/12. В таком случае среднее квадратическое отклонение случ числа равно 
.
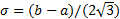Закон Пуассона.
P(X=m) =(a^m) /m! * e ^-alfa