ДИФРАКЦИЯ СВЕТА
· Радиус зон Френеля в случае плоского волнового фронта:
 ,
,
где rk - радиус зоны (Рис. 16), k – номер зоны (k = 1,2,3,…), L – расстояние от круглого отверстия в непрозрачном экране до точки наблюдения, расположенной на оси отверстия,  длина световой волны.
длина световой волны.

· Дифракция на одной щели (дифракция Фраунгофера):
а) направления, в которых амплитуда колебаний дифракционных лучей минимальна, определяется из условия
 ; k = 1, 2, 3, …,
; k = 1, 2, 3, …,
где a – ширина щели, 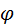 - угол отклонения лучей от нормали к плоскости щели,
- угол отклонения лучей от нормали к плоскости щели,  – порядковый номер минимума,
– порядковый номер минимума,  -длина световой волны.
-длина световой волны.
б) направления, в которых амплитуда колебаний дифракционных лучей максимальна, определяется из условия
 ; k = 1, 2, 3, …,
; k = 1, 2, 3, …,
· Дифракция на плоской решетке:
Направления, в которых наблюдается максимум света, определяется из условия
 ; k =1,2,3…,
; k =1,2,3…,
где d – период решетки, 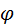 - угол отклонения лучей от нормали к плоскости щели,
- угол отклонения лучей от нормали к плоскости щели,  – порядковый номер максимума,
– порядковый номер максимума,  - длина световой волны.
- длина световой волны.
Примеры решения задач
Пример 13. На щель шириной a = 0,08 мм падает нормально монохроматический свет (λ= 0,56 мкм). Определить угол отклонения лучей, соответствующих первой светлой дифракционной полосе расположенной левее (или правее) центрального максимума?
Дано:
 а = 0,08 мм
λ= 0,56 мкм а = 0,08 мм
λ= 0,56 мкм
| Решение:
В направлении  после диафрагмы разность хода между параллельными лучами равна ВС (рис.9). Разбивая фронт волны в плоскости щели на зоны Френеля, получим их число: после диафрагмы разность хода между параллельными лучами равна ВС (рис.9). Разбивая фронт волны в плоскости щели на зоны Френеля, получим их число:
|
 -? -?
|



где а – ширина щели,  - направление дифракции, λ – длина волны
- направление дифракции, λ – длина волны
Условия максимума будут наблюдаться в тех направлениях, в которых число зон Френеля будет нечетным

В нашем случае k = 1, тогда

Подставляя числовые значения физических величин, найдем:
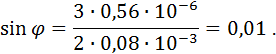
Этому значению синуса соответствует угол  0⁰34ʹ
0⁰34ʹ
Пример 14. На дифракционную решетку в направлении нормали к ее поверхности падает монохроматический свет. Период решетки d = 2 мкм. Какого наибольшего порядка дифракционный максимум дает эта решетка в случае красного ( l1 = 0,7 мкм) и в случае фиолетового (l2 = 0,41 мкм) света?
| Дано: d = 2 мкм l1 = 0,7 мкм l2 = 0,41 мкм | Решение:
Запишем условия максимума интенсивности света при дифракции на плоской решетке
 (1)
где d – период решетки, (1)
где d – период решетки, 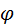 - угол отклонения лучей от нормали к плоскости щели, - угол отклонения лучей от нормали к плоскости щели,  – порядковый номер максимума, – порядковый номер максимума,  - длина световой волны. - длина световой волны.
|
| k -? |
Из выражения (1) получим:  (2)
(2)
sinjне может быть больше 1, поэтому, как это следует из формулы (2), число k не может быть больше d/l, т.е.
k £ d/l. (3)
Подставив в формулу (3) числовые значения, получим:
- для красных лучей k £ 2/0,7 = 2,86;
- для фиолетовых лучей k£ 2/0,41 = 4,88.
Если учесть, что порядок максимумов является целым числом, то для красного света kmax = 2и для фиолетового kmax = 4.
Задачи для самостоятельного решения
051. Вычислить радиус пятидесятой зоны Френеля для плоского волнового фронта (λ = 0,5 мкм), если построение делается для точки наблюдения, находящейся на расстоянии 1 м от фронта волны.
R = 0,5 см
052. Радиус четвертой зоны Френеля для плоского волнового фронта равен 3 мм. Определить радиус двадцать пятой зоны.
R = 7,5 мм
053. Найти радиус третьей зоны Френеля, если расстояние от источника света до волновой поверхности 1 м, а расстояние от волновой поверхности до точки наблюдения 1м. Длина волны света 500 нм.
R = 0, 86 мм
054. На щель шириной 0, 05 мм падает нормально монохроматический свет (λ = 0,6 мкм). Определить угол между первоначальным направлением лучей и на четвертую темную дифракционную полосу.
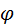 = 2⁰45ʹ
= 2⁰45ʹ
055. На узкую щель падает нормально монохроматический свет. Угол отклонения лучей, соответствующих второй светлой дифракционной полосе, равен одному градусу. Скольким длинам волн падающего света равна ширина щели?
 143
143
056.Сколько штрихов на каждый миллиметр содержит дифракционная решетка, если при наблюдении в монохроматическом свете (λ = 0,6 мкм) максимум пятого порядка отклонен на угол 180?
n = 103
057. Какое количество штрихов на единицу длины имеет дифракционная решетка, если зеленая линия ртути (λ = 546,1 нм) в спектре первого порядка наблюдается под углом  ?
?
n = 600 мм-1
058. На дифракционную решетку нормально падает пучок света от разрядной трубки, наполненной гелием. На какую линию l2 в спектре третьего порядка накладывается красная линия гелия (λ1 = 670 нм) спектра второго порядка?
λ2 = 447 нм – синяя линия
059. Определить длину волны для линии в дифракционном спектре третьего порядка, совпадающей с изображением линии в спектре четвертого порядка с длиной волны λ4 = 490 нм.
λ3 = 653 нм
060.Какой наибольший порядок спектра можно видеть в дифракционной решетке, имеющей 500 штрихов на 1 мм, при освещении ее светом с длиной волны λ = 720 нм?
k = 2
ФОТОМЕТРИЯ
· Световой поток Ф, испускаемый точечным источником:
 ,
,
 – телесный угол, I – сила света источника, находящегося в вершине телесного угла.
– телесный угол, I – сила света источника, находящегося в вершине телесного угла.
а) полный световой поток точечного источника
 I.
I.
· Освещенность Е поверхности равна:

где Ф – световой поток, S – площадь поверхности.
а) освещенность, создаваемая точечным источником на расстоянии r от него, равна:
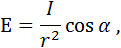
где  – угол падения лучей.
– угол падения лучей.
· Светимость R равномерно светящейся поверхности равна:

где Ф – световой поток, испускаемый с поверхности,  площадь поверхности.
площадь поверхности.
· Размерность физических величин в фотометрии:
а) Ф – световой поток. Измеряется в люменах (лм).
б) I – сила света. Измеряется в канделах (кд).
в) Е – освещенность. Измеряется в люксах (лк).
г)  - светимость. Измеряется в
- светимость. Измеряется в 
д)  – телесный угол. Измеряется в стерадианах (ср).
– телесный угол. Измеряется в стерадианах (ср).
Примеры решения задач
Пример 15. Светильник из молочного стекла имеет форму шара диаметром 24 см. В центре светильника находится лампа силой света 100 кд. Определить светимость шара.
| Дано: D = 0,24 м I = 100 кд | Решение:
Светимость светильника равна:
 где Ф – световой поток, испускаемый с поверхности светильника,
где Ф – световой поток, испускаемый с поверхности светильника,  площадь сферической поверхности. площадь сферической поверхности.
|
| R =? |
Будем считать лампу точечным источником света. Тогда полный световой поток испускаемый лампой равен:
 I. (2)
I. (2)
Будем также пренебрегать потерей света при его прохождении сквозь матовое стекло светильника. Тогда с поверхности светильника будет испускаться точно такой же световой поток. Подставляя формулу (2) в формулу (1) получим:

Подставляя численные значения физических величин в формулу (3) получим:

Пример 16. Над центром круглого стола радиусом 70 cм на высоте 1,5 м висит лампа силой света 120 кд. Определить освещенность на краю стола.
| Дано: R = 0,7 м h = 1,5 м I = 120 кд | Решение:
Принимая лампу за точечный источник света, найдем освещенность на краю стола по формуле:

|
| Е -? |
Из рис. 10 видно, что величины  равны соответственно:
равны соответственно:  (2)
(2)

|  (3)
Подставляя формулы (3) и (2) в формулу (1), получим: (3)
Подставляя формулы (3) и (2) в формулу (1), получим:
 Подставим численные значения.
Подставим численные значения.

|