Учебный модуль 7. Последовательности и ряды. Тема 15. Числовые ряды.
ЛЕКЦИЯ 15. Числовые ряды. Признаки сходимости числовых рядов.
Пусть дана функция 
. Если областью определения функции является множество натуральных чисел 
, то мы говорим, что значения функции образуют бесконечную числовую последовательность
.
называется общим членом последовательности. Для сокращения записи вводится обозначение 
. Тогда последовательность можно записать так
u 1, u 2, u 3 ,..., un … (15.1)
Замечание. Областью определения функция может быть и множество натуральных чисел с добавлением нуля 
.
Пусть задана бесконечная числовая последовательность чисел (15.1). Числовым рядом называется последовательность чисел, члены которой соединены знаком плюс, т.е. выражение
u 1 + u 2 + u 3 +... + un +... = 
. (15.2)
числа u 1, u 2, u 3,..., u n,... называются членами ряда, а u n общим членом ряда.
Например, числовой ряд
имеет общий член un = 
Сходимость и сумма ряда. Частичной суммой Sn называется сумма первых n членов ряда, т.е.
Частичные суммы ряда образуют новую последовательность - последовательность частичных сумм S 1, S 2, S 3,..., S n,.... Если существует конечный предел последовательности частичных сумм 
= S < ¥, то ряд (15.2) называется сходящимся, а число S - суммой ряда. В этом случае пишут 
. Если такой предел не существует или равен бесконечности, то ряд называют расходящимся.
Разность между рядом и его частичной суммой называется остатком ряда и обозначается 
.
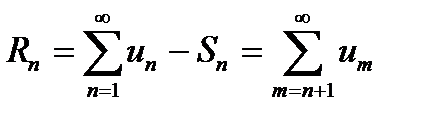или 
Пример 1. Определить сходимость ряда
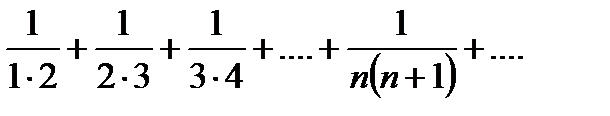
Решение. Напишем частичную сумму заданного ряда
Каждое из слагаемых представим в виде суммы простейших так, как это делали в интегралах
|
|
Числители выражений слева и справа равны, подставляя в равенство корни знаменателя, найдем А и В
то есть
.
Применим формулу к каждому члену частичной суммы ряда
Рассмотрим предел частичных сумм
Следовательно, ряд сходится и его сумма равна 1.
Пример 2. Дан числовой ряд
исследовать сходимость ряда.
Решение. Члены ряда положительны. Заменим в частичной сумме каждое слагаемое на последнее 
, тем самым уменьшим частичную сумму
Величина 
бесконечно возрастает с ростом n. Поэтому предел последовательности Sn при n ® ¥ равен бесконечности и ряд расходится.
Пример 3. Определить сходимость следующего ряда:
1 - 1 + 1 - 1 + (-1) n +1 +....
Решение. Четная частичная сумма этого ряда S 2 n = 0, а нечетная - S 2 n +1 = 1. Это означает, что предел 
не существует. Следовательно, данный ряд расходится.
Теорема о необходимом условии (признаке) сходимости числового ряда. Если числовой ряд сходится, то его общий член при n ® ¥ стремится к нулю, т.е.
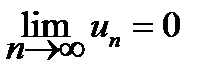(15.3)
Доказательство. Рассмотрим две соседние частичные суммы ряда (15.2)
Sn- 1 = u 1 + u 2 + u 3 +... un- 1,
Sn = u 1 + u 2 + u 3 +... u n -1 + un = Sn- 1 + un.
Из сходимости ряда следует, что
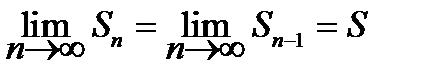
С другой стороны, по теоремам о пределах,
т.е.
S = S +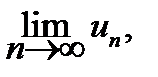 
откуда и следует (15.2) .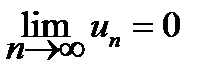
Введенное условие сходимости является лишь необходимым, но не достаточным. Это означает, что существуют расходящиеся ряды, у которых 
.
Пример. Ряд, рассмотренный в примере 2
Расходится, но его общий член стремится к нулю. Действительно
Аналогичным свойством обладает гармонический ряд, который будет рассмотрен ниже.
Основные свойства сходящихся числовых рядов.
|
|
Свойство 1. Ряд и его остаток сходятся и расходятся одновременно. Действительно, частичная сумма ряда при фиксированном n есть число. Рассмотрим сумму m слагаемых 
.
.
Рассмотрим предел этого выражения при 
. Так как предел постоянной равен самой постоянной, а 
от m не зависит и является величиной постоянной, то
.
Оба предела одновременно конечны или бесконечны.
Следствие. Добавление или отбрасывание конечного числа членов не изменяет сходимости ряда.
Свойство 2. При умножении ряда на число с его сходимость не меняется. Докажем свойство для сходящихся рядов. Если ряд
u 1 + u 2 + u 3 +... + un +... = .
сходится и имеет сумму S, то ряд
cu 1 + cu 2 +... + cun +..,
также сходится и имеет сумму с∙S.
Доказательство. Рассмотрим частичную сумму ряда
sn = cu 1 + cu 2 + cu 3 +... + cun = cSn.
Поэтому
Свойство 3. Сходящиеся ряды можно почленно складывать и вычитать.
Доказательство. Пусть
u 1 + u 2 + u 3 +... + un +... = S;
v 1 + v 2 + v 3 +... + vn +... = Ф,
тогда ряд
(u 1± v 1) + (u 2 ± v 2) +... + (un ± vn) +...
также сходится и имеет сумму S ± Ф, так как предел суммы равен сумме пределов
Замечание. При сложении сходящегося и расходящегося ряда суммарный ряд тоже будет расходится.