Равномерное и показательное распределения НСВ: функция распределения, плотность, основные параметры распределения, числовые характеристики, вероятность попадания на интервал.
| M(X) | D(X) | σ(X) | |||
| Равномерный
| 
| 
| 
| 
| Ошибка округления до ближайшего целого деления.
Время ожидания транспорта с постоянным интервалом движения.

|
| y |
| b |
| y =F(x) |
| x |
| Рис. 2.11. Функция распределения F(x) равномерной случайной величины |
| а |
| x |
| а |
| b |
| c |
| f(x) |
| Рис.2.10. Плотность вероятности f(x) равномерной случайной величины |
| x |
| F(x) |
| y = f(x) |
Постоянная  , т. к. по свойству плотности вероятности площадь криволинейной трапеции, опирающейся на отрезок [a, b], должна быть равна 1.
, т. к. по свойству плотности вероятности площадь криволинейной трапеции, опирающейся на отрезок [a, b], должна быть равна 1.
 График
График  изображен на рис. 2.11.
изображен на рис. 2.11.
| M(X) | D(X) | σ(X) | ||||
|  
| 
| 
| 
| Время безотказной работы прибора; продолжительность телефонного разговора

|
т.к  >0, =>,
>0, =>,  . График
. График  изображен на рис. 2.12.
изображен на рис. 2.12.
| 2.13. Функция распределенияпоказ.закона |

|
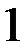
|

|

|

|

|

|

|

|
| 2.12. Плотностьпоказательного закона |

|
.
11. Непрерывная случайная величина называется нормально распределенной с параметрами  , если её плотность вероятности задается формулой:
, если её плотность вероятности задается формулой: 
Функция распределения F(x) нормальной случайной величины

Теорема. Если непрерывная случайная величина Х нормально распределена c плотностью вероятности, то её числовые характеристики равны: 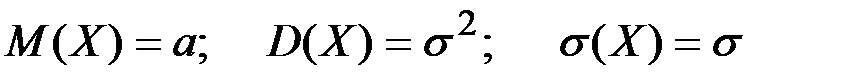
 .
.
Для нормально распределенной случайной величины Х имеют место следующие свойства.
Свойство 1. Для нормально распределенной случайной величины с параметрами 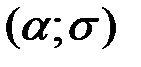 вероятность попадания на промежуток
вероятность попадания на промежуток  вычисляется по формуле:
вычисляется по формуле: 
Доказательство. По свойству плотности вероятности, свойству интеграла и равенству (2.11) имеем:


Ч.т.д
Свойство 2. Для нормально распределенной случайной величины Х с параметрами  вероятность отклонения Х от своего среднего значения а меньше, чем на
вероятность отклонения Х от своего среднего значения а меньше, чем на  , вычисляется по формуле
, вычисляется по формуле
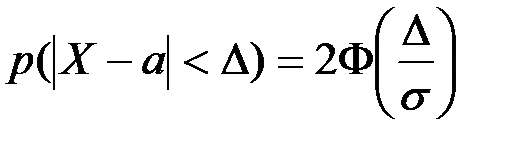 .
.
Доказательство. Используя равенство (2.12)и нечетность функции Лапласа, получаем требуемое:


Свойство 3. Правило трех сигма. Все значения нормально распределенной случайной величины с практической достоверностью лежат в интервале  , т. е.
, т. е. 
Доказательство: 
Свойство 4. Пусть  – независимые нормальные случайные величины с параметрами
– независимые нормальные случайные величины с параметрами  . Тогда случайная величина
. Тогда случайная величина  также нормально распределена и
также нормально распределена и 
12) Распределение χ2 Пирсона, F- распределение Фишера, t- распределение Стьюдента; основные параметры этих распределений, графики.
Распределение Пирсона  (xu – квадрат)
(xu – квадрат)
 где
где  ~
~ 
 ;
; 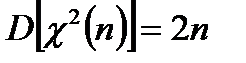
 , где
, где 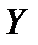 ~
~ 
 ;
; 
Распределение Фишера-Снедекора (F – распределение)
 ;
; 
Неравенства Маркова и Чебышева, лемма о среднем арифметическом случ.величин.
Неравенство Маркова: Если Х – неотрицательная НСВ ( ), тогда
), тогда 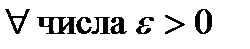 справедливо неравенство
справедливо неравенство  .
.
Неравенство Чебышева: Пусть Х – СВ с числовыми характеристиками  и
и  , тогда
, тогда  справедливо неравенство
справедливо неравенство  .
.
О среднем арифметическом: Если  независимые однотипные CВ с математическим ожиданием а и дисперсией D, тогда
независимые однотипные CВ с математическим ожиданием а и дисперсией D, тогда  справедливо неравенство
справедливо неравенство
 .
.
Закон больших чисел. Центральная предельная теорема.
Закон больших чисел: Если  независимые однотипные CВ с математическим ожиданием а, тогда
независимые однотипные CВ с математическим ожиданием а, тогда 
 .
.
Центральная предельная теорема – это группа теорем об условиях, при которых возникает нормальный закон распределения.
При изучении нормального закона была сформулирована теорема: если  – независимые нормальные случайные величины с одними и теми же параметрами
– независимые нормальные случайные величины с одними и теми же параметрами  и
и  , то их сумма
, то их сумма  также нормальна и имеет параметры
также нормальна и имеет параметры  и
и  . Кроме того, справедливо равенстводля любого сколь угодно малого числа
. Кроме того, справедливо равенстводля любого сколь угодно малого числа  . Это равенство практически точно уже при
. Это равенство практически точно уже при  .
.
 Ф
Ф 
Это утверждение называется центральной предельной теоремой и кратко формулируется так: сумма большого числа независимых однотипных случайных величин с любым законом распределения приближенно нормальна.
теорема Ляпунова: если случайные величины независимы и никакая из них не доминирует над другими, то при достаточно большом числе слагаемых их сумма приближенно нормальна.
 -незав. СВ
-незав. СВ
MX=a, DX=σ2 ; 
15. Двумерная СВ-упорядоченная пара СВ (Х;Y)
Коэффициентом корреляции случайной величины (Х,Y) называется число  , равное:
, равное: 
Ковариацией (корреляционным моментом) случайной величины (Х,Y) называется число  , равное:
, равное:  .
.
Числовыми хар-ми двумерной СВ (Х;Y) считают числхар-кикаждой из ее компонент, а также числхар-ки, определяющие тесноту связи между компонентами ковариация, коэф-т корреляции.
16. Генеральной совокупностью называется совокупность объектов, из которых производится выборка. Выборочной совокупностью (выборкой) называется совокупность случайно отобранных объектов из генеральной совокупности.
Вариационный ряд- ранжированная(упорядоченная) по возраст или убыв выборка.
Статистический ряд- двойной ряд чисел, указывающий каким образом знач-я признака(вер-ти) связаны с их повторяемостью(частотами) в выбранной стат совок-ти.
17. Выборочная (эмпири́ческая) фу́нкцияраспределе́ния в математической статистике - это приближение теоретической функции распределения, построенное с помощью выборки из него.
Функция  , определяющая для каждого значения х относительную частоту события
, определяющая для каждого значения х относительную частоту события  , называется эмпирической функцией распределения или функцией распределения выборки.
, называется эмпирической функцией распределения или функцией распределения выборки.
18. Ломаная, отрезки которой соединяют точки  , называется полигоном частот. Ломаная, соединяющая на координатной плоскости точки
, называется полигоном частот. Ломаная, соединяющая на координатной плоскости точки  , называется полигоном относительных частот.
, называется полигоном относительных частот.
Полигон относительных частот для распределения показа
| Рис. 3.3. Гистограмма частот |

|
| x |
| Рис. 3.2. Полигон относительных частот |
| 0,1 |
| 0,2 |
| 0,3 |
|
| х |
Ступенчатая фигура, состоящая из прямоугольников с основаниями длиной  и высотами
и высотами  (плотность частоты), называется гистограммой частот. (рис. 3.3)
(плотность частоты), называется гистограммой частот. (рис. 3.3)
19. Несмещенной называется статистическая оценка  , математическое ожидание которой равно оцениваемому параметру
, математическое ожидание которой равно оцениваемому параметру  при любой выборке:
при любой выборке:
 (3.6)
(3.6)
Смещенной называется оценка, при которой условие (3.6) не выполняется.
Эффективной называется оценка, которая имеет минимальную дисперсию при заданном объеме выборки п.
Состоятельной называется статистическая оценка типа (3.4), которая при  стремится к оцениваемому параметру.
стремится к оцениваемому параметру.
 (3.4)
(3.4)
20. виды числовых характеристик оценок:
выборочная средняя 
Если значения признака  в выборке имеют соответственно частоты
в выборке имеют соответственно частоты  , то последнюю формулу можно переписать в виде
, то последнюю формулу можно переписать в виде
 (3.7)
(3.7)
Выборочная средняя (3.7) является состоятельной несмещенной оценкой математического ожидания случайной величины, т. е. 
Введем в рассмотрение величины, характеризующие отклонение количественного признака Х от своего среднего значения. Одной из них является исправленная выборочная дисперсия
 (3.8)
(3.8)
Исправленная выборочная дисперсия (3.8) является состоятельной несмещенной оценкой дисперсии случайной величины, т.е.  Если в формуле (3.8) знаменатель
Если в формуле (3.8) знаменатель  заменить на
заменить на  , то оценка останется состоятельной, но будет смещенной, т.е.
, то оценка останется состоятельной, но будет смещенной, т.е. 
В случае, когда математическое ожидание признака Х известно:  , в качестве состоятельной несмещенной оценки для дисперсии можно использовать выборочную дисперсию
, в качестве состоятельной несмещенной оценки для дисперсии можно использовать выборочную дисперсию
 (3.9)
(3.9)
Аналогично вводятся оценки для среднего квадратического отклонения: 