Классическое определение вероятности

№1. На эк­за­мен вы­не­се­но 60 во­про­сов, Ан­дрей не вы­учил 3 из них. Най­ди­те ве­ро­ят­ность того, что ему по­па­дет­ся вы­учен­ный во­прос.

№ 2. На та­рел­ке 16 пи­рож­ков: 7 с рыбой, 5 с ва­ре­ньем и 4 с виш­ней. Юля на­у­гад вы­би­ра­ет один пи­ро­жок. Най­ди­те ве­ро­ят­ность того, что он ока­жет­ся с виш­ней.

№ 3. В слу­чай­ном экс­пе­ри­мен­те бро­са­ют две иг­раль­ные кости. Най­ди­те ве­ро­ят­ность того, что в сумме вы­па­дет 8 очков. Ре­зуль­тат округ­ли­те до сотых.

№ 4. В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют два­жды. Най­ди­те ве­ро­ят­ность того, что орел вы­па­дет ровно один раз.

№ 5. При про­из­вод­стве в сред­нем на каж­дые 2982 ис­прав­ных на­со­са при­хо­дит­ся 18 не­ис­прав­ных. Най­ди­те ве­ро­ят­ность того, что слу­чай­но вы­бран­ный насос ока­жет­ся не­ис­прав­ным.

№ 6. На­уч­ная кон­фе­рен­ция про­во­дит­ся в 5 дней. Всего за­пла­ни­ро­ва­но 75 до­кла­дов — пер­вые три дня по 17 до­кла­дов, осталь­ные рас­пре­де­ле­ны по­ров­ну между чет­вер­тым и пятым днями. По­ря­док до­кла­дов опре­де­ля­ет­ся же­ребьёвкой. Ка­ко­ва ве­ро­ят­ность, что до­клад про­фес­со­ра М. ока­жет­ся за­пла­ни­ро­ван­ным на по­след­ний день кон­фе­рен­ции?

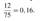Ре­ше­ние. За пер­вые три дня будет про­чи­тан 51 до­клад, на по­след­ние два дня пла­ни­ру­ет­ся 24 до­кла­да. По­это­му на по­след­ний день за­пла­ни­ро­ва­но 12 до­кла­дов. Зна­чит, ве­ро­ят­ность того, что до­клад про­фес­со­ра М. ока­жет­ся за­пла­ни­ро­ван­ным на по­след­ний день кон­фе­рен­ции, равна

Ответ: 0,16.

№ 7. Кон­курс ис­пол­ни­те­лей про­во­дит­ся в 5 дней. Всего за­яв­ле­но 80 вы­ступ­ле­ний — по од­но­му от каж­дой стра­ны, участ­ву­ю­щей в кон­кур­се. Ис­пол­ни­тель из Рос­сии участ­ву­ет в кон­кур­се. В пер­вый день за­пла­ни­ро­ва­но 8 вы­ступ­ле­ний, осталь­ные рас­пре­де­ле­ны по­ров­ну между остав­ши­ми­ся днями. По­ря­док вы­ступ­ле­ний опре­де­ля­ет­ся же­ребьёвкой. Ка­ко­ва ве­ро­ят­ность, что вы­ступ­ле­ние ис­пол­ни­те­ля из Рос­сии со­сто­ит­ся в тре­тий день кон­кур­са?

Ре­ше­ние. На тре­тий день за­пла­ни­ро­ва­но (80 - 8): 4 =18 вы­ступ­ле­ний. Зна­чит, ве­ро­ят­ность того, что вы­ступ­ле­ние пред­ста­ви­те­ля из Рос­сии ока­жет­ся за­пла­ни­ро­ван­ным на тре­тий день кон­кур­са, равна 18/80 = 0,225

Ответ: 0,225.

№ 8. На кон­фе­рен­цию при­е­ха­ли 3 уче­ных из Нор­ве­гии, 3 из Рос­сии и 4 из Ис­па­нии. Каж­дый из них де­ла­ет на кон­фе­рен­ции один до­клад. По­ря­док до­кла­дов опре­де­ля­ет­ся же­ребьёвкой. Най­ди­те ве­ро­ят­ность того, что вось­мым ока­жет­ся до­клад уче­но­го из Рос­сии.

№ 9. Перед на­ча­лом пер­во­го тура чем­пи­о­на­та по бад­мин­то­ну участ­ни­ков раз­би­ва­ют на иг­ро­вые пары слу­чай­ным об­ра­зом с по­мо­щью жре­бия. Всего в чем­пи­о­на­те участ­ву­ет 26 бад­мин­то­ни­стов, среди ко­то­рых 10 спортс­ме­нов из Рос­сии, в том числе Рус­лан Орлов. Най­ди­те ве­ро­ят­ность того, что в пер­вом туре Рус­лан Орлов будет иг­рать с каким-либо бад­мин­то­ни­стом из Рос­сии.

Ре­ше­ние. В пер­вом туре Рус­лан Орлов может сыг­рать с 26 − 1 = 25 бад­мин­то­ни­ста­ми, из ко­то­рых 10 − 1 = 9 из Рос­сии. Зна­чит, ве­ро­ят­ность того, что в пер­вом туре Рус­лан Орлов будет иг­рать с каким-либо бад­мин­то­ни­стом из Рос­сии, равна

Ответ: 0,36.

№ 10. В сбор­ни­ке би­ле­тов по био­ло­гии всего 55 би­ле­тов, в 11 из них встре­ча­ет­ся во­прос по теме "Бо­та­ни­ка". Най­ди­те ве­ро­ят­ность того, что в слу­чай­но вы­бран­ном на эк­за­ме­не би­ле­те школь­ни­ку до­ста­нет­ся во­прос по теме "Бо­та­ни­ка".

Ответ: 0,2.

№ 11. В чем­пи­о­на­те мира участ­ву­ют 16 ко­манд. С по­мо­щью жре­бия их нужно раз­де­лить на че­ты­ре груп­пы по че­ты­ре ко­ман­ды в каж­дой. В ящике впе­ре­меш­ку лежат кар­точ­ки с но­ме­ра­ми групп:

1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Ка­пи­та­ны ко­манд тянут по одной кар­точ­ке. Ка­ко­ва ве­ро­ят­ность того, что ко­ман­да Рос­сии ока­жет­ся во вто­рой груп­пе?

№ 12. На кла­ви­а­ту­ре те­ле­фо­на 10 цифр, от 0 до 9. Ка­ко­ва ве­ро­ят­ность того, что слу­чай­но на­жа­тая цифра будет чётной?

Ре­ше­ние. На кла­ви­а­ту­ре те­ле­фо­на 10 цифр, из них 5 чет­ных: 0, 2, 4, 6, 8. По­это­му ве­ро­ят­ность того, что слу­чай­но будет на­жа­та чет­ная цифра, равна 5: 10 = 0,5.

Ответ: 0,5.

№ 13. Из мно­же­ства на­ту­раль­ных чисел от 10 до 19 на­уда­чу вы­би­ра­ют одно число. Ка­ко­ва ве­ро­ят­ность того, что оно де­лит­ся на 3?

Ре­ше­ние. На­ту­раль­ных чисел от 10 до 19 де­сять, из них на три де­лят­ся три числа: 12, 15, 18. Сле­до­ва­тель­но, ис­ко­мая ве­ро­ят­ность равна 3:10 = 0,3.

Ответ: 0,3.

№ 14. В груп­пе ту­ри­стов 5 че­ло­век. С по­мо­щью жре­бия они вы­би­ра­ют двух че­ло­век, ко­то­рые долж­ны идти в село в ма­га­зин за про­дук­та­ми. Ка­ко­ва ве­ро­ят­ность того, что ту­рист Д., вхо­дя­щий в со­став груп­пы, пойдёт в ма­га­зин?

№ 15. Перед на­ча­лом фут­боль­но­го матча судья бро­са­ет мо­нет­ку, чтобы опре­де­лить, какая из ко­манд начнёт игру с мячом. Ко­ман­да «Физик» иг­ра­ет три матча с раз­ны­ми ко­ман­да­ми. Най­ди­те ве­ро­ят­ность того, что в этих играх «Физик» вы­иг­ра­ет жре­бий ровно два раза.

Ре­ше­ние. Обо­зна­чим «1» ту сто­ро­ну мо­не­ты, ко­то­рая от­ве­ча­ет за вы­иг­рыш жре­бия «Фи­зи­ком», дру­гую сто­ро­ну мо­не­ты обо­зна­чим «0». Тогда бла­го­при­ят­ных ком­би­на­ций три: 110, 101, 011, а всего ком­би­на­ций 2³ = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, ис­ко­мая ве­ро­ят­ность равна:

Ответ: 0,375.

№ 16. Иг­раль­ный кубик бро­са­ют два­жды. Сколь­ко эле­мен­тар­ных ис­хо­дов опыта бла­го­при­ят­ству­ют со­бы­тию «А = сумма очков равна 5»?

Ре­ше­ние. Сумма очков может быть равна 5 в че­ты­рех слу­ча­ях: «3 + 2», «2 + 3», «1 + 4», «4 + 1».

Ответ: 4.

№ 17. В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют два­жды. Най­ди­те ве­ро­ят­ность того, что на­сту­пит исход ОР (в пер­вый раз вы­па­да­ет орёл, во вто­рой — решка).

Ре­ше­ние. Всего воз­мож­ных ис­хо­дов — че­ты­ре: орел-орел, орел-решка, решка-орел, решка-решка. Бла­го­при­ят­ным яв­ля­ет­ся один: орел-решка. Сле­до­ва­тель­но, ис­ко­мая ве­ро­ят­ность равна 1: 4 = 0,25.

Ответ: 0,25.

№ 18. На рок-фе­сти­ва­ле вы­сту­па­ют груп­пы — по одной от каж­дой из за­яв­лен­ных стран. По­ря­док вы­ступ­ле­ния опре­де­ля­ет­ся жре­би­ем. Ка­ко­ва ве­ро­ят­ность того, что груп­па из Дании будет вы­сту­пать после груп­пы из Шве­ции и после груп­пы из Нор­ве­гии? Ре­зуль­тат округ­ли­те до сотых.

Ре­ше­ние.

Общее ко­ли­че­ство вы­сту­па­ю­щих на фе­сти­ва­ле групп для от­ве­та на во­прос не­важ­но. Сколь­ко бы их ни было, для ука­зан­ных стран есть 6 спо­со­бов вза­им­но­го рас­по­ло­же­ния среди вы­сту­па­ю­щих (Д — Дания, Ш — Шве­ция, Н — Нор­ве­гия):

...Д...Ш...Н...,...Д...Н...Ш...,...Ш...Н...Д...,...Ш...Д...Н...,...Н...Д...Ш...,...Н...Ш...Д...

Дания на­хо­дит­ся после Шве­ции и Нор­ве­гии в двух слу­ча­ях. По­это­му ве­ро­ят­ность того, что груп­пы слу­чай­ным об­ра­зом будут рас­пре­де­ле­ны имен­но так, равна

Ответ: 0,33.

№ 19. В не­ко­то­ром го­ро­де из 5000 по­явив­ших­ся на свет мла­ден­цев 2512 маль­чи­ков. Най­ди­те ча­сто­ту рож­де­ния де­во­чек в этом го­ро­де. Ре­зуль­тат округ­ли­те до ты­сяч­ных.

Ре­ше­ние. Из 5000 тысяч но­во­рож­ден­ных 5000 − 2512 = 2488 де­во­чек. По­это­му ча­сто­та рож­де­ния де­во­чек равна Ответ: 0,498.

№ 20. На борту самолёта 12 кре­сел рас­по­ло­же­ны рядом с за­пас­ны­ми вы­хо­да­ми и 18 — за пе­ре­го­род­ка­ми, раз­де­ля­ю­щи­ми са­ло­ны. Все эти места удоб­ны для пас­са­жи­ра вы­со­ко­го роста. Осталь­ные места не­удоб­ны. Пас­са­жир В. вы­со­ко­го роста. Най­ди­те ве­ро­ят­ность того, что на ре­ги­стра­ции при слу­чай­ном вы­бо­ре места пас­са­жи­ру В. до­ста­нет­ся удоб­ное место, если всего в самолёте 300 мест.

Ре­ше­ние. В са­мо­ле­те 12 + 18 = 30 мест удоб­ны пас­са­жи­ру В., а всего в са­мо­ле­те 300 мест. По­это­му ве­ро­ят­ность того, что пас­са­жи­ру В. до­ста­нет­ся удоб­ное место равна 30: 300 = 0,1.

Ответ: 0,1.

№ 21. На олим­пиа­де по рус­ско­му языку 250 участ­ни­ков раз­ме­сти­ли в трёх ауди­то­ри­ях. В пер­вых двух уда­лось раз­ме­стить по 120 че­ло­век, остав­ших­ся пе­ре­ве­ли в за­пас­ную ауди­то­рию в дру­гом кор­пу­се. Най­ди­те ве­ро­ят­ность того, что слу­чай­но вы­бран­ный участ­ник писал олим­пи­а­ду в за­пас­ной ауди­то­рии.

Ре­ше­ние. Всего в за­пас­ную ауди­то­рию на­пра­ви­ли 250 − 120 − 120 = 10 че­ло­век. По­это­му ве­ро­ят­ность того, что слу­чай­но вы­бран­ный участ­ник писал олим­пи­а­ду в за­пас­ной ауди­то­рии, равна 10: 250 = 0,04.

Ответ: 0,04.

№ 22. В клас­се 26 уча­щих­ся, среди них два друга — Ан­дрей и Сер­гей. Уча­щих­ся слу­чай­ным об­ра­зом раз­би­ва­ют на 2 рав­ные груп­пы. Най­ди­те ве­ро­ят­ность того, что Ан­дрей и Сер­гей ока­жут­ся в одной груп­пе.

Ре­ше­ние. Пусть один из дру­зей на­хо­дит­ся в не­ко­то­рой груп­пе. Вме­сте с ним в груп­пе ока­жут­ся 12 че­ло­век из 25 остав­ших­ся од­но­класс­ни­ков. Ве­ро­ят­ность того, что вто­рой друг ока­жет­ся среди этих 12 че­ло­век, равна 12: 25 = 0,48.

№ 23. В фирме такси в на­ли­чии 50 лег­ко­вых ав­то­мо­би­лей; 27 из них чёрного цвета с жёлтыми над­пи­ся­ми на бор­тах, осталь­ные — жёлтого цвета с чёрными над­пи­ся­ми. Най­ди­те ве­ро­ят­ность того, что на слу­чай­ный вызов при­е­дет ма­ши­на жёлтого цвета с чёрными над­пи­ся­ми.

№ 31. В груп­пе ту­ри­стов 30 че­ло­век. Их вер­толётом в не­сколь­ко приёмов за­бра­сы­ва­ют в труд­но­до­ступ­ный район по 6 че­ло­век за рейс. По­ря­док, в ко­то­ром вер­толёт пе­ре­во­зит ту­ри­стов, слу­ча­ен. Най­ди­те ве­ро­ят­ность того, что ту­рист П. по­ле­тит пер­вым рей­сом вер­толёта.

№ 24. Ве­ро­ят­ность того, что новый DVD-про­иг­ры­ва­тель в те­че­ние года по­сту­пит в га­ран­тий­ный ре­монт, равна 0,045. В не­ко­то­ром го­ро­де из 1000 про­дан­ных DVD-про­иг­ры­ва­те­лей в те­че­ние года в га­ран­тий­ную ма­стер­скую по­сту­пи­ла 51 штука. На сколь­ко от­ли­ча­ет­ся ча­сто­та со­бы­тия «га­ран­тий­ный ре­монт» от его ве­ро­ят­но­сти в этом го­ро­де?

Ре­ше­ние. Ча­сто­та (от­но­си­тель­ная ча­сто­та) со­бы­тия «га­ран­тий­ный ре­монт» равна 51: 1000 = 0,051. Она от­ли­ча­ет­ся от пред­ска­зан­ной ве­ро­ят­но­сти на 0,006.

Ответ: 0,006.

№ 25. В кар­ма­не у Миши было че­ты­ре кон­фе­ты — «Гри­льяж», «Бе­лоч­ка», «Ко­ров­ка» и «Ла­сточ­ка», а также ключи от квар­ти­ры. Вы­ни­мая ключи, Миша слу­чай­но вы­ро­нил из кар­ма­на одну кон­фе­ту. Най­ди­те ве­ро­ят­ность того, что по­те­ря­лась кон­фе­та «Гри­льяж».

№ 34. Ме­ха­ни­че­ские часы с две­на­дца­ти­ча­со­вым ци­фер­бла­том в какой-то мо­мент сло­ма­лись и пе­ре­ста­ли идти. Най­ди­те ве­ро­ят­ность того, что ча­со­вая стрел­ка оста­но­ви­лась, до­стиг­нув от­мет­ки 10, но не дойдя до от­мет­ки 1.

Ре­ше­ние. На ци­фер­бла­те между де­ся­тью ча­са­ми и одним часом три ча­со­вых де­ле­ния. Всего на ци­фер­бла­те 12 ча­со­вых де­ле­ний. По­это­му ис­ко­мая ве­ро­ят­ность равна:

Ответ: 0,25.

№ 35. За круг­лый стол на 9 сту­льев в слу­чай­ном по­ряд­ке рас­са­жи­ва­ют­ся 7 маль­чи­ков и 2 де­воч­ки. Най­ди­те ве­ро­ят­ность того, что обе де­воч­ки будут си­деть рядом.

Ре­ше­ние. Пусть пер­вой за стол сядет де­воч­ка, рядом с ней есть два места, на каж­дое из ко­то­рых может сесть 8 че­ло­век, из ко­то­рых толь­ко одна де­воч­ка. Таким об­ра­зом ве­ро­ят­ность, что де­воч­ки будут си­деть рядом равна

Ответ: 0,25.

№ 36. За круг­лый стол на 5 сту­льев в слу­чай­ном по­ряд­ке рас­са­жи­ва­ют­ся 3 маль­чи­ка и 2 де­воч­ки. Най­ди­те ве­ро­ят­ность того, что де­воч­ки будут си­деть рядом.

Ре­ше­ние. Пусть пер­вой за стол сядет де­воч­ка, тогда рядом с ней есть два места, на каж­дое из ко­то­рых пре­тен­ду­ет 4 че­ло­ве­ка, из ко­то­рых толь­ко одна де­воч­ка. Таким об­ра­зом ве­ро­ят­ность, что де­воч­ки будут си­деть рядом равна 2*0,25=0,5.

№ 37. За круг­лый стол на 201 стул в слу­чай­ном по­ряд­ке рас­са­жи­ва­ют­ся 199 маль­чи­ков и 2 де­воч­ки. Най­ди­те ве­ро­ят­ность того, что между де­воч­ка­ми будет си­деть один маль­чик.

Ре­ше­ние. Рас­смот­рим си­дя­щую за сто­лом де­воч­ку. За сто­лом есть два места через одно от нее, на каж­дое из ко­то­рых пре­тен­ду­ет 200 че­ло­век, из ко­то­рых толь­ко одна де­воч­ка. Таким об­ра­зом, ве­ро­ят­ность, что между двумя де­воч­ка­ми будет си­деть один маль­чик равна 2 * 0,01 = 0,02

Ответ: 0,01

№ 38. За круг­лый стол на 9 сту­льев в слу­чай­ном по­ряд­ке рас­са­жи­ва­ют­ся 7 маль­чи­ков и 2 де­воч­ки. Най­ди­те ве­ро­ят­ность того, что де­воч­ки не будут си­деть рядом.

Ре­ше­ние. Пусть пер­вой за стол сядет де­воч­ка, тогда рядом с ней есть два места, на каж­дое из ко­то­рых пре­тен­ду­ет 8 че­ло­ве­ка, из ко­то­рых толь­ко одна де­воч­ка. Таким об­ра­зом, ве­ро­ят­ность того, что де­воч­ки будут си­деть рядом равна 0,25. А ве­ро­ят­ность того, что де­воч­ки не будут си­деть рядом равна 0,75.

Ответ: 0,75

№ 39. За круг­лый стол на 17 сту­льев в слу­чай­ном по­ряд­ке рас­са­жи­ва­ют­ся 15 маль­чи­ков и 2 де­воч­ки. Най­ди­те ве­ро­ят­ность того, что де­воч­ки будут си­деть рядом.

Ре­ше­ние. Пусть пер­вой за стол сядет де­воч­ка, тогда рядом с ней есть два места, на каж­дое из ко­то­рых пре­тен­ду­ет 16 че­ло­ве­ка, из ко­то­рых толь­ко одна де­воч­ка. Таким об­ра­зом, ве­ро­ят­ность, что де­воч­ки будут си­деть рядом равна 0,125.

№ 44. У Дины в ко­пил­ке лежит 7 рублёвых, 5 двух­рублёвых, 6 пя­ти­рублёвых и 2 де­ся­ти­рублёвых мо­не­ты. Дина на­у­гад достаёт из ко­пил­ки одну мо­не­ту. Най­ди­те ве­ро­ят­ность того, что ­остав­ша­я­ся в ко­пил­ке сумма со­ста­вит менее 60 руб­лей.

Ре­ше­ние. У Дины в ко­пил­ке лежит 7 + 5 + 6 + 2 = 20 монет на сумму 7 + 10 + 30 + 20 = 67 руб­лей. Менее 60 руб­лей оста­нет­ся, если до­стать из ко­пил­ки де­ся­ти­рублёвую мо­не­ту. Ис­ко­мая ве­ро­ят­ность равна 2: 20 = 0,1.

Ответ: 0,1.

№ 45. На чем­пи­о­на­те по прыж­кам в воду вы­сту­па­ют 20 спортс­ме­нов, среди них 3 пры­гу­на из Чехии и 2 пры­гу­на из Бо­ли­вии. По­ря­док вы­ступ­ле­ний опре­де­ля­ет­ся же­ре­бьев­кой. Най­ди­те ве­ро­ят­ность того, что две­на­дца­тым будет вы­сту­пать пры­гун из Чехии.

№ 46. В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют три­жды. Най­ди­те ве­ро­ят­ность того, что вы­па­дет хотя бы две решки.

Ре­ше­ние. Всего воз­мож­ных ис­хо­дов — 8: орел-орел-орел, орел-орел-решка, орел-решка-решка, орел-решка-орел, решка-решка-решка, решка-решка-орел, решка-орел-орел, решка-орел-решка. Бла­го­при­ят­ны­ми яв­ля­ют­ся че­ты­ре: решка-решка-решка, решка-решка-орел, решка-орел-решка, орел-решка-решка. Сле­до­ва­тель­но, ис­ко­мая ве­ро­ят­ность равна 4: 8 = 0,5.

Ответ: 0,5.

№ 47. Ме­ха­ни­че­ские часы с две­на­дца­ти­ча­со­вым ци­фер­бла­том в какой-то мо­мент сло­ма­лись и пе­ре­ста­ли идти. Най­ди­те ве­ро­ят­ность того, что ча­со­вая стрел­ка оста­но­ви­лась, до­стиг­нув от­мет­ки 4, но не дойдя до от­мет­ки 7 часов.

Ре­ше­ние. На ци­фер­бла­те между де­ся­тью ча­са­ми и одним часом три ча­со­вых де­ле­ния. Всего на ци­фер­бла­те 12 ча­со­вых де­ле­ний. По­это­му ис­ко­мая ве­ро­ят­ность равна:

Ответ: 0,25.

№ 48. Ме­ха­ни­че­ские часы с две­на­дца­ти­ча­со­вым ци­фер­бла­том в какой-то мо­мент сло­ма­лись и пе­ре­ста­ли идти. Най­ди­те ве­ро­ят­ность того, что ча­со­вая стрел­ка оста­но­ви­лась, до­стиг­нув от­мет­ки 8, но не дойдя до от­мет­ки 11 часов.

Ре­ше­ние. На ци­фер­бла­те между во­се­мью и один­на­дца­тью ча­са­ми три ча­со­вых де­ле­ния. Всего на ци­фер­бла­те 12 ча­со­вых де­ле­ний. По­это­му ис­ко­мая ве­ро­ят­ность равна:

Ответ: 0,25.

№ 49. Перед на­ча­лом пер­во­го тура чем­пи­о­на­та по бад­мин­то­ну участ­ни­ков раз­би­ва­ют на иг­ро­вые пары слу­чай­ным об­ра­зом с по­мо­щью жре­бия. Всего в чем­пи­о­на­те участ­ву­ет 76 бад­мин­то­ни­стов, среди ко­то­рых 16 спортс­ме­нов из Рос­сии, в том числе Игорь Чаев. Ка­ко­ва ве­ро­ят­ность того, что в пер­вом туре Игорь Чаев будет иг­рать с каким-либо бад­мин­то­ни­стом из Рос­сии.

Ре­ше­ние. В пер­вом туре Игорь Чаев может сыг­рать с 76 − 1 = 75 бад­мин­то­ни­ста­ми, из ко­то­рых 16 − 1 = 15 из Рос­сии. Зна­чит, ве­ро­ят­ность того, что в пер­вом туре Игорь Чаев будет иг­рать с каким-либо бад­мин­то­ни­стом из Рос­сии, равна

Ответ: 0,2.