Теоремы о вероятностях событий

№ 1. Ве­ро­ят­ность того, что ба­та­рей­ка бра­ко­ван­ная, равна 0,06. По­ку­па­тель в ма­га­зи­не вы­би­ра­ет слу­чай­ную упа­ков­ку, в ко­то­рой две таких ба­та­рей­ки. Най­ди­те ве­ро­ят­ность того, что обе ба­та­рей­ки ока­жут­ся ис­прав­ны­ми.

Ре­ше­ние. Ве­ро­ят­ность того, что ба­та­рей­ка ис­прав­на, равна 0,94. Ве­ро­ят­ность про­из­ве­де­ния не­за­ви­си­мых со­бы­тий (обе ба­та­рей­ки ока­жут­ся ис­прав­ны­ми) равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий: 0,94·0,94 = 0,8836.

Ответ: 0,8836.

№ 2. Ка­ко­ва ве­ро­ят­ность того, что слу­чай­но вы­бран­ный те­ле­фон­ный номер окан­чи­ва­ет­ся двумя чётными циф­ра­ми?

Ре­ше­ние. Ве­ро­ят­ность того, что на одном из тре­бу­е­мых мест ока­жет­ся чётное число равна 0,5. Сле­до­ва­тель­но, ве­ро­ят­ность того, что на двух ме­стах од­но­вре­мен­но ока­жут­ся два чётных числа равна 0,5 · 0,5=0,25.

Ответ: 0,25.

№ 3. Ве­ро­ят­ность того, что новый элек­три­че­ский чай­ник про­слу­жит боль­ше года, равна 0,93. Ве­ро­ят­ность того, что он про­слу­жит боль­ше двух лет, равна 0,87. Най­ди­те ве­ро­ят­ность того, что он про­слу­жит мень­ше двух лет, но боль­ше года.

Ре­ше­ние. Пусть A = «чай­ник про­слу­жит боль­ше года, но мень­ше двух лет», В = «чай­ник про­слу­жит боль­ше двух лет», С = «чай­ник про­слу­жит ровно два года», тогда A + B + С = «чай­ник про­слу­жит боль­ше года».

Со­бы­тия A, В и С не­сов­мест­ные, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий. Ве­ро­ят­ность со­бы­тия С, со­сто­я­ще­го в том, что чай­ник вый­дет из строя ровно через два года — стро­го в тот же день, час и се­кун­ду — равна нулю. Тогда:

P(A + B+ С) = P(A) + P(B)+ P(С)= P(A) + P(B),

от­ку­да, ис­поль­зуя дан­ные из усло­вия, по­лу­ча­ем

0,93 = P(A) + 0,87.

Тем самым, для ис­ко­мой ве­ро­ят­но­сти имеем:

P(A) = 0,93 − 0,87 = 0,06.

Ответ: 0,06.

№ 4. Из рай­он­но­го цен­тра в де­рев­ню еже­днев­но ходит ав­то­бус. Ве­ро­ят­ность того, что в по­не­дель­ник в ав­то­бу­се ока­жет­ся мень­ше 18 пас­са­жи­ров, равна 0,82. Ве­ро­ят­ность того, что ока­жет­ся мень­ше 10 пас­са­жи­ров, равна 0,51. Най­ди­те ве­ро­ят­ность того, что число пас­са­жи­ров будет от 10 до 17.

Ре­ше­ние. Рас­смот­рим со­бы­тия A = «в ав­то­бу­се мень­ше 10 пас­са­жи­ров» и В = «в ав­то­бу­се от 10 до 17 пас­са­жи­ров». Их сумма — со­бы­тие A + B = «в ав­то­бу­се мень­ше 18 пас­са­жи­ров». Со­бы­тия A и В не­сов­мест­ные, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий:

P(A + B) = P(A) + P(B).

Тогда, ис­поль­зуя дан­ные за­да­чи, по­лу­ча­ем: 0,82 = 0,51 + P(В), от­ку­да P(В) = 0,82 − 0,51 = 0,31.

Ответ: 0,31.

№ 5.Ве­ро­ят­ность того, что на те­сти­ро­ва­нии по ма­те­ма­ти­ке уча­щий­ся П. верно решит боль­ше 12 задач, равна 0,7. Ве­ро­ят­ность того, что П. верно решит боль­ше 11 задач, равна 0,79. Най­ди­те ве­ро­ят­ность того, что П. верно решит ровно 12 задач.

Ре­ше­ние. Рас­смот­рим со­бы­тия A = «уча­щий­ся решит 12 задач» и В = «уча­щий­ся решит боль­ше 12 задач». Их сумма — со­бы­тие A + B = «уча­щий­ся решит боль­ше 11 задач». Со­бы­тия A и В не­сов­мест­ные, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий:

P(A + B) = P(A) + P(B).

Тогда, ис­поль­зуя дан­ные за­да­чи, по­лу­ча­ем: 0,79 = P(A) + 0,7, от­ку­да P(A) = 0,79 − 0,7 = 0,09.

Ответ: 0,09.

№ 6. Если шах­ма­тист А. иг­ра­ет бе­лы­ми фи­гу­ра­ми, то он вы­иг­ры­ва­ет у шах­ма­ти­ста Б. с ве­ро­ят­но­стью 0,5. Если А. иг­ра­ет чер­ны­ми, то А. вы­иг­ры­ва­ет у Б. с ве­ро­ят­но­стью 0,3. Шах­ма­ти­сты А. и Б. иг­ра­ют две пар­тии, причём во вто­рой пар­тии ме­ня­ют цвет фигур. Най­ди­те ве­ро­ят­ность того, что А. вы­иг­ра­ет оба раза.

Ре­ше­ние. Воз­мож­ность вы­иг­рать первую и вто­рую пар­тию не за­ви­сят друг от друга. Ве­ро­ят­ность про­из­ве­де­ния не­за­ви­си­мых со­бы­тий равна про­из­ве­де­нию их ве­ро­ят­но­стей: 0,5 · 0,3 = 0,15.

Ответ: 0,15.

№ 7. В ма­га­зи­не три про­дав­ца. Каж­дый из них занят с кли­ен­том с ве­ро­ят­но­стью 0,3. Най­ди­те ве­ро­ят­ность того, что в слу­чай­ный мо­мент вре­ме­ни все три про­дав­ца за­ня­ты од­но­вре­мен­но (счи­тай­те, что кли­ен­ты за­хо­дят не­за­ви­си­мо друг от друга).

Ре­ше­ние. Ве­ро­ят­ность про­из­ве­де­ния не­за­ви­си­мых со­бы­тий равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий. По­это­му ве­ро­ят­ность того, что все три про­дав­ца за­ня­ты равна. Ответ: 0,027.

№ 8. На ри­сун­ке изоб­ражён ла­би­ринт. Паук за­пол­за­ет в ла­би­ринт в точке «Вход». Раз­вер­нуть­ся и полз­ти назад паук не может, по­это­му на каж­дом раз­ветв­ле­нии паук вы­би­ра­ет один из путей, по ко­то­ро­му ещё не полз. Счи­тая, что выбор даль­ней­ше­го пути чисто слу­чай­ный, опре­де­ли­те, с какой ве­ро­ят­но­стью паук придёт к вы­хо­ду.

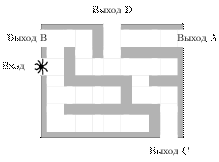
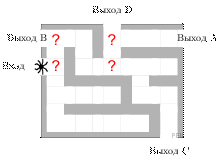
Ре­ше­ние. На каж­дой из че­ты­рех от­ме­чен­ных раз­ви­лок паук с ве­ро­ят­но­стью 0,5 может вы­брать или путь, ве­ду­щий к вы­хо­ду D, или дру­гой путь. Это не­за­ви­си­мые со­бы­тия, ве­ро­ят­ность их про­из­ве­де­ния (паук дой­дет до вы­хо­да D) равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий. По­это­му ве­ро­ят­ность прий­ти к вы­хо­ду D равна (0,5)⁴ = 0,0625.

Ответ: 0,0625.

№ 9. В тор­го­вом цен­тре два оди­на­ко­вых ав­то­ма­та про­да­ют кофе. Об­слу­жи­ва­ние ав­то­ма­тов про­ис­хо­дит по ве­че­рам после за­кры­тия цен­тра. Из­вест­но, что ве­ро­ят­ность со­бы­тия «К ве­че­ру в пер­вом ав­то­ма­те за­кон­чит­ся кофе» равна 0,25. Такая же ве­ро­ят­ность со­бы­тия «К ве­че­ру во вто­ром ав­то­ма­те за­кон­чит­ся кофе». Ве­ро­ят­ность того, что кофе к ве­че­ру за­кон­чит­ся в обоих ав­то­ма­тах, равна 0,15. Най­ди­те ве­ро­ят­ность того, что к ве­че­ру дня кофе оста­нет­ся в обоих ав­то­ма­тах.

Ре­ше­ние. Рас­смот­рим со­бы­тия

А = кофе за­кон­чит­ся в пер­вом ав­то­ма­те,

В = кофе за­кон­чит­ся во вто­ром ав­то­ма­те.

Тогда

A·B = кофе за­кон­чит­ся в обоих ав­то­ма­тах,

A + B = кофе за­кон­чит­ся хотя бы в одном ав­то­ма­те.

По усло­вию P(A) = P(B) = 0,3; P(A·B) = 0,15.

Со­бы­тия A и B сов­мест­ные, ве­ро­ят­ность суммы двух сов­мест­ных со­бы­тий равна сумме ве­ро­ят­но­стей этих со­бы­тий, умень­шен­ной на ве­ро­ят­ность их про­из­ве­де­ния:

P(A + B) = P(A) + P(B) − P(A·B) = 0,25 + 0,25 − 0,15 = 0,35.

Сле­до­ва­тель­но, ве­ро­ят­ность про­ти­во­по­лож­но­го со­бы­тия, со­сто­я­ще­го в том, что кофе оста­нет­ся в обоих ав­то­ма­тах, равна 1 − 0,35 = 0,65.

Ответ: 0,65.

При­ве­дем дру­гое ре­ше­ние.

Ве­ро­ят­ность того, что кофе оста­нет­ся в пер­вом ав­то­ма­те равна 1 − 0,25 = 0,75. Ве­ро­ят­ность того, что кофе оста­нет­ся во вто­ром ав­то­ма­те равна 1 − 0,25 = 0,75. Ве­ро­ят­ность того, что кофе оста­нет­ся в пер­вом или вто­ром ав­то­ма­те равна 1 − 0,15 = 0,85. По­сколь­ку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,85 = 0,75 + 0,75 − х, от­ку­да ис­ко­мая ве­ро­я­тость х = 0,65.

№ 10. Ве­ро­ят­ность того, что в слу­чай­ный мо­мент вре­ме­ни тем­пе­ра­ту­ра тела здо­ро­во­го че­ло­ве­ка ока­жет­ся ниже чем 36,8 °С, равна 0,81. Най­ди­те ве­ро­ят­ность того, что в слу­чай­ный мо­мент вре­ме­ни у здо­ро­во­го че­ло­ве­ка тем­пе­ра­ту­ра ока­жет­ся 36,8 °С или выше.

Ре­ше­ние. Ука­зан­ные со­бы­тия про­ти­во­по­лож­ны, по­это­му ис­ко­мая ве­ро­ят­ность равна 1 − 0,81 = 0,19.

№ 11. При из­го­тов­ле­нии под­шип­ни­ков диа­мет­ром 67 мм ве­ро­ят­ность того, что диа­метр будет от­ли­чать­ся от за­дан­но­го не боль­ше, чем на 0,01 мм, равна 0,965. Най­ди­те ве­ро­ят­ность того, что слу­чай­ный под­шип­ник будет иметь диа­метр мень­ше чем 66,99 мм или боль­ше чем 67,01 мм.

Ре­ше­ние. По усло­вию, диа­метр под­шип­ни­ка будет ле­жать в пре­де­лах от 66,99 до 67,01 мм с ве­ро­ят­но­стью 0,965. По­это­му ис­ко­мая ве­ро­ят­ность про­ти­во­по­лож­но­го со­бы­тия равна 1 − 0,965 = 0,035.

Ответ: 0,035.

№ 12. Би­ат­ло­нист пять раз стре­ля­ет по ми­ше­ням. Ве­ро­ят­ность по­па­да­ния в ми­шень при одном вы­стре­ле равна 0,8. Най­ди­те ве­ро­ят­ность того, что би­ат­ло­нист пер­вые три раза попал в ми­ше­ни, а по­след­ние два про­мах­нул­ся. Ре­зуль­тат округ­ли­те до сотых.

Ре­ше­ние. По­сколь­ку би­ат­ло­нист по­па­да­ет в ми­ше­ни с ве­ро­ят­но­стью 0,8, он про­ма­хи­ва­ет­ся с ве­ро­ят­но­стью 1 − 0,8 = 0,2. Cобы­тия по­пасть или про­мах­нуть­ся при каж­дом вы­стре­ле не­за­ви­си­мы, ве­ро­ят­ность про­из­ве­де­ния не­за­ви­си­мых со­бы­тий равна про­из­ве­де­нию их ве­ро­ят­но­стей. Тем самым, ве­ро­ят­ность со­бы­тия «попал, попал, попал, про­мах­нул­ся, про­мах­нул­ся» равна 0,8 * 0,8 * 0,8 * 0,2 * 0.2 =. (примерно 0,02)

Ответ: 0,02.

№ 13.По­ме­ще­ние осве­ща­ет­ся фонарём с двумя лам­па­ми. Ве­ро­ят­ность пе­ре­го­ра­ния лампы в те­че­ние года равна 0,3. Най­ди­те ве­ро­ят­ность того, что в те­че­ние года хотя бы одна лампа не пе­ре­го­рит.

Ре­ше­ние. Най­дем ве­ро­ят­ность того, что пе­ре­го­рят обе лампы. Эти со­бы­тия не­за­ви­си­мые, ве­ро­ят­ность их про­из­ве­де­ния равно про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий: 0,3·0,3 = 0,09.

Со­бы­тие, со­сто­я­щее в том, что не пе­ре­го­рит хотя бы одна лампа, про­ти­во­по­лож­ное. Сле­до­ва­тель­но, его ве­ро­ят­ность равна 1 − 0,09 = 0,91.

Ответ: 0,91.

№ 14. При ар­тил­ле­рий­ской стрель­бе ав­то­ма­ти­че­ская си­сте­ма де­ла­ет вы­стрел по цели. Если цель не уни­что­же­на, то си­сте­ма де­ла­ет по­втор­ный вы­стрел. Вы­стре­лы по­вто­ря­ют­ся до тех пор, пока цель не будет уни­что­же­на. Ве­ро­ят­ность уни­что­же­ния не­ко­то­рой цели при пер­вом вы­стре­ле равна 0,4, а при каж­дом по­сле­ду­ю­щем — 0,6. Сколь­ко вы­стре­лов по­тре­бу­ет­ся для того, чтобы ве­ро­ят­ность уни­что­же­ния цели была не менее 0,98? В от­ве­те ука­жи­те наи­мень­шее не­об­хо­ди­мое ко­ли­че­ство вы­стре­лов.

Ре­ше­ние. Най­дем ве­ро­ят­ность про­ти­во­по­лож­но­го со­бы­тия, со­сто­я­ще­го в том, что цель не будет уни­что­же­на за n вы­стре­лов. Ве­ро­ят­ность про­мах­нуть­ся при пер­вом вы­стре­ле равна 0,6, а при каж­дом сле­ду­ю­щем — 0,4. Эти со­бы­тия не­за­ви­си­мые, ве­ро­ят­ность их про­из­ве­де­ния равна про­из­ве­де­нию ве­ро­ят­но­сти этих со­бы­тий. По­это­му ве­ро­ят­ность про­мах­нуть­ся при n вы­стре­лах равна: Оста­лось найти наи­мень­шее на­ту­раль­ное ре­ше­ние не­ра­вен­ства По­сле­до­ва­тель­но про­ве­ряя зна­че­ния, рав­ные 1, 2, 3 и т. д. на­хо­дим, что ис­ко­мым ре­ше­ни­ем яв­ля­ет­ся. Сле­до­ва­тель­но, не­об­хо­ди­мо сде­лать 5 вы­стре­лов.

Ответ: 5.

При­ме­ча­ние. Можно ре­шать за­да­чу «по дей­стви­ям», вы­чис­ляя ве­ро­ят­ность уце­леть после ряда по­сле­до­ва­тель­ных про­ма­хов:

Р(1) = 0,6.

Р(2) = Р(1)·0,4 = 0,24.

Р(3) = Р(2)·0,4 = 0,096.

Р(4) = Р(3)·0,4 = 0,0384;

Р(5) = Р(4)·0,4 = 0,01536.

По­след­няя ве­ро­ят­ность мень­ше 0,02, по­это­му до­ста­точ­но пяти вы­стре­лов по ми­ше­ни.

При­ве­дем дру­гое ре­ше­ние.

№ 15. На эк­за­ме­не по гео­мет­рии школь­ник от­ве­ча­ет на один во­прос из спис­ка эк­за­ме­на­ци­он­ных во­про­сов. Ве­ро­ят­ность того, что это во­прос по теме «Впи­сан­ная окруж­ность», равна 0,2. Ве­ро­ят­ность того, что это во­прос по теме «Па­рал­ле­ло­грамм», равна 0,15. Во­про­сов, ко­то­рые од­но­вре­мен­но от­но­сят­ся к этим двум темам, нет. Най­ди­те ве­ро­ят­ность того, что на эк­за­ме­не школь­ни­ку до­ста­нет­ся во­прос по одной из этих двух тем.

Ре­ше­ние. Ве­ро­ят­ность суммы двух не­сов­мест­ных со­бы­тий равна сумме ве­ро­ят­но­стей этих со­бы­тий: 0,2 + 0,15 = 0,35.

Ответ: 0,35.

№ 16. Чтобы прой­ти в сле­ду­ю­щий круг со­рев­но­ва­ний, фут­боль­ной ко­ман­де нужно на­брать хотя бы 4 очка в двух играх. Если ко­ман­да вы­иг­ры­ва­ет, она по­лу­ча­ет 3 очка, в слу­чае ни­чьей — 1 очко, если про­иг­ры­ва­ет — 0 очков. Най­ди­те ве­ро­ят­ность того, что ко­ман­де удаст­ся выйти в сле­ду­ю­щий круг со­рев­но­ва­ний. Счи­тай­те, что в каж­дой игре ве­ро­ят­но­сти вы­иг­ры­ша и про­иг­ры­ша оди­на­ко­вы и равны 0,4.

Ре­ше­ние. Ко­ман­да может по­лу­чить не мень­ше 4 очков в двух играх тремя спо­со­ба­ми: 3+1, 1+3, 3+3. Эти со­бы­тия не­сов­мест­ны, ве­ро­ят­ность их суммы равна сумме их ве­ро­ят­но­стей. Каж­дое из этих со­бы­тий пред­став­ля­ет собой про­из­ве­де­ние двух не­за­ви­си­мых со­бы­тий — ре­зуль­та­та в пер­вой и во вто­рой игре. От­сю­да имеем 1 - 0,4 - 0,4 = 0,2; Р(в) * Р(н) + Р(в) * Р(в) + Р(н) *Р(в) = 0,4*0,2+0,4*0,4+0.4*0,2= 0,32

Ответ: 0,32.

№ 17. В Вол­шеб­ной стра­не бы­ва­ет два типа по­го­ды: хо­ро­шая и от­лич­ная, причём по­го­да, уста­но­вив­шись утром, дер­жит­ся не­из­мен­ной весь день. Из­вест­но, что с ве­ро­ят­но­стью 0,8 по­го­да зав­тра будет такой же, как и се­год­ня. Се­год­ня 3 июля, по­го­да в Вол­шеб­ной стра­не хо­ро­шая. Най­ди­те ве­ро­ят­ность того, что 6 июля в Вол­шеб­ной стра­не будет от­лич­ная по­го­да.

Ре­ше­ние. Для по­го­ды на 4, 5 и 6 июля есть 4 ва­ри­ан­та: ХХО, ХОО, ОХО, ООО (здесь Х — хо­ро­шая, О — от­лич­ная по­го­да). Най­дем ве­ро­ят­но­сти на­ступ­ле­ния такой по­го­ды:

P(XXO) = 0,8·0,8·0,2 = 0,128;

P(XOO) = 0,8·0,2·0,8 = 0,128;

P(OXO) = 0,2·0,2·0,2 = 0,008;

P(OOO) = 0,2·0,8·0,8 = 0,128.

 

Ука­зан­ные со­бы­тия не­сов­мест­ные, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий:

P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392.

Ответ: 0,392.

№ 18. В ма­га­зи­не стоят два платёжных ав­то­ма­та. Каж­дый из них может быть не­ис­пра­вен с ве­ро­ят­но­стью 0,05 не­за­ви­си­мо от дру­го­го ав­то­ма­та. Най­ди­те ве­ро­ят­ность того, что хотя бы один ав­то­мат ис­пра­вен.

Ре­ше­ние. Най­дем ве­ро­ят­ность того, что не­ис­прав­ны оба ав­то­ма­та. Эти со­бы­тия не­за­ви­си­мые, ве­ро­ят­ность их про­из­ве­де­ния равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий: 0,05 · 0,05 = 0,0025.

Со­бы­тие, со­сто­я­щее в том, что ис­пра­вен хотя бы один ав­то­мат, про­ти­во­по­лож­ное. Сле­до­ва­тель­но, его ве­ро­ят­ность равна 1 − 0,0025 = 0,9975.

Ответ: 0,9975.

№ 19. В тор­го­вом цен­тре два оди­на­ко­вых ав­то­ма­та про­да­ют кофе. Ве­ро­ят­ность того, что к концу дня в ав­то­ма­те за­кон­чит­ся кофе, равна 0,3. Ве­ро­ят­ность того, что кофе за­кон­чит­ся в обоих ав­то­ма­тах, равна 0,12. Най­ди­те ве­ро­ят­ность того, что к концу дня кофе оста­нет­ся в обоих ав­то­ма­тах.

Ре­ше­ние. Рас­смот­рим со­бы­тия

А = кофе за­кон­чит­ся в пер­вом ав­то­ма­те,

В = кофе за­кон­чит­ся во вто­ром ав­то­ма­те.

Тогда

A·B = кофе за­кон­чит­ся в обоих ав­то­ма­тах,

A + B = кофе за­кон­чит­ся хотя бы в одном ав­то­ма­те.

 

По усло­вию P(A) = P(B) = 0,3; P(A·B) = 0,12.

Со­бы­тия A и B сов­мест­ные, ве­ро­ят­ность суммы двух сов­мест­ных со­бы­тий равна сумме ве­ро­ят­но­стей этих со­бы­тий, умень­шен­ной на ве­ро­ят­ность их про­из­ве­де­ния:

P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48.

 

Сле­до­ва­тель­но, ве­ро­ят­ность про­ти­во­по­лож­но­го со­бы­тия, со­сто­я­ще­го в том, что кофе оста­нет­ся в обоих ав­то­ма­тах, равна 1 − 0,48 = 0,52.

Ответ: 0,52.

При­ве­дем дру­гое ре­ше­ние.

Ве­ро­ят­ность того, что кофе оста­нет­ся в пер­вом ав­то­ма­те равна 1 − 0,3 = 0,7. Ве­ро­ят­ность того, что кофе оста­нет­ся во вто­ром ав­то­ма­те равна 1 − 0,3 = 0,7. Ве­ро­ят­ность того, что кофе оста­нет­ся в пер­вом или вто­ром ав­то­ма­те равна 1 − 0,12 = 0,88. По­сколь­ку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, от­ку­да ис­ко­мая ве­ро­я­тость х = 0,52.

№ 20. Две фаб­ри­ки вы­пус­ка­ют оди­на­ко­вые стек­ла для ав­то­мо­биль­ных фар. Пер­вая фаб­ри­ка вы­пус­ка­ет 45% этих сте­кол, вто­рая — 55%. Пер­вая фаб­ри­ка вы­пус­ка­ет 3% бра­ко­ван­ных сте­кол, а вто­рая — 1%. Най­ди­те ве­ро­ят­ность того, что слу­чай­но куп­лен­ное в ма­га­зи­не стек­ло ока­жет­ся бра­ко­ван­ным.

Ре­ше­ние.

Ве­ро­ят­ность того, что стек­ло сде­ла­но на пер­вой фаб­ри­ке и оно бра­ко­ван­ное: 0,45 · 0,03 = 0,0135.

Ве­ро­ят­ность того, что стек­ло сде­ла­но на вто­рой фаб­ри­ке и оно бра­ко­ван­ное: 0,55 · 0,01 = 0,0055.

По­это­му по фор­му­ле пол­ной ве­ро­ят­но­сти ве­ро­ят­ность того, что слу­чай­но куп­лен­ное в ма­га­зи­не стек­ло ока­жет­ся бра­ко­ван­ным равна 0,0135 + 0,0055 = 0,019.

Ответ: 0,019.

№ 21. Ков­бой Джон по­па­да­ет в муху на стене с ве­ро­ят­но­стью 0,9, если стре­ля­ет из при­стре­лян­но­го ре­воль­ве­ра. Если Джон стре­ля­ет из не­при­стре­лян­но­го ре­воль­ве­ра, то он по­па­да­ет в муху с ве­ро­ят­но­стью 0,2. На столе лежит 10 ре­воль­ве­ров, из них толь­ко 4 при­стре­лян­ные. Ков­бой Джон видит на стене муху, на­уда­чу хва­та­ет пер­вый по­пав­ший­ся ре­воль­вер и стре­ля­ет в муху. Най­ди­те ве­ро­ят­ность того, что Джон про­махнётся.

Ре­ше­ние. Джон про­мах­нет­ся, если схва­тит при­стре­лян­ный ре­воль­вер и про­мах­нет­ся из него, или если схва­тит не­при­стре­лян­ный ре­воль­вер и про­мах­нет­ся из него. По фор­му­ле услов­ной ве­ро­ят­но­сти, ве­ро­ят­но­сти этих со­бы­тий равны со­от­вет­ствен­но 0,4·(1 − 0,9) = 0,04 и 0,6·(1 − 0,2) = 0,48. Эти со­бы­тия не­сов­мест­ны, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий: 0,04 + 0,48 = 0,52.

Ответ: 0,52.

№ 22. Аг­ро­фир­ма за­ку­па­ет ку­ри­ные яйца в двух до­маш­них хо­зяй­ствах. 40% яиц из пер­во­го хо­зяй­ства — яйца выс­шей ка­те­го­рии, а из вто­ро­го хо­зяй­ства — 20% яиц выс­шей ка­те­го­рии. Всего выс­шую ка­те­го­рию по­лу­ча­ет 35% яиц. Най­ди­те ве­ро­ят­ность того, что яйцо, куп­лен­ное у этой аг­ро­фир­мы, ока­жет­ся из пер­во­го хо­зяй­ства.

Ре­ше­ние. Это ре­ше­ние можно за­пи­сать ко­рот­ко. Пусть х — ис­ко­мая ве­ро­ят­ность того, что куп­ле­но яйцо, про­из­ве­ден­ное в пер­вом хо­зяй­стве. Тогда 1 - х — ве­ро­ят­ность того, что куп­ле­но яйцо, про­из­ве­ден­ное во вто­ром хо­зяй­стве. По фор­му­ле пол­ной ве­ро­ят­но­сти имеем: 0,4 х * 0,2 (1-х) =0,35

Ответ: 0,75.

№ 23. На фаб­ри­ке ке­ра­ми­че­ской по­су­ды 10% про­из­ведённых та­ре­лок имеют де­фект. При кон­тро­ле ка­че­ства про­дук­ции вы­яв­ля­ет­ся 80% де­фект­ных та­ре­лок. Осталь­ные та­рел­ки по­сту­па­ют в про­да­жу. Най­ди­те ве­ро­ят­ность того, что слу­чай­но вы­бран­ная при по­куп­ке та­рел­ка не имеет де­фек­тов. Ре­зуль­тат округ­ли­те до сотых.

Ре­ше­ние. Пусть завод про­из­вел n та­ре­лок. В про­да­жу по­сту­пят все ка­че­ствен­ные та­рел­ки и 20% не­вы­яв­лен­ных де­фект­ных та­ре­лок: 0,9n+0,2*0,1n = 0,98 та­ре­лок. По­сколь­ку ка­че­ствен­ных из них 0,9n, ве­ро­ят­ность ку­пить ка­че­ствен­ную та­рел­ку равна 0,9n/0,98n=0,98

Ответ: 0,98.

№ 25. Ве­ро­ят­ность того, что на те­сти­ро­ва­нии по био­ло­гии уча­щий­ся О. верно решит боль­ше 11 задач, равна 0,67. Ве­ро­ят­ность того, что О. верно решит боль­ше 10 задач, равна 0,74. Най­ди­те ве­ро­ят­ность того, что О. верно решит ровно 11 задач.

Ре­ше­ние.

Рас­смот­рим со­бы­тия A = «уча­щий­ся решит 11 задач» и В = «уча­щий­ся решит боль­ше 11 задач». Их сумма — со­бы­тие A + B = «уча­щий­ся решит боль­ше 10 задач». Со­бы­тия A и В не­сов­мест­ные, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий: P(A + B) = P(A) + P(B).

Тогда, ис­поль­зуя дан­ные за­да­чи, по­лу­ча­ем: 0,74 = P(A) + 0,67, от­ку­да P(A) = 0,74 − 0,67 = 0,07.

Ответ: 0,07.

№ 26. По от­зы­вам по­ку­па­те­лей Иван Ива­но­вич оце­нил надёжность двух ин­тер­нет-ма­га­зи­нов. Ве­ро­ят­ность того, что нуж­ный товар до­ста­вят из ма­га­зи­на А, равна 0,8. Ве­ро­ят­ность того, что этот товар до­ста­вят из ма­га­зи­на Б, равна 0,9. Иван Ива­но­вич за­ка­зал товар сразу в обоих ма­га­зи­нах. Счи­тая, что ин­тер­нет-ма­га­зи­ны ра­бо­та­ют не­за­ви­си­мо друг от друга, най­ди­те ве­ро­ят­ность того, что ни один ма­га­зин не до­ста­вит товар.

Ре­ше­ние. Ве­ро­ят­ность того, что пер­вый ма­га­зин не до­ста­вит товар равна 1 − 0,9 = 0,1. Ве­ро­ят­ность того, что вто­рой ма­га­зин не до­ста­вит товар равна 1 − 0,8 = 0,2. По­сколь­ку эти со­бы­тия не­за­ви­си­мы, ве­ро­ят­ность их про­из­ве­де­ния (оба ма­га­зи­на не до­ста­вят товар) равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий: 0,1 · 0,2 = 0,02.

Ответ: 0,02.

№ 27. Перед на­ча­лом во­лей­боль­но­го матча ка­пи­та­ны ко­манд тянут чест­ный жре­бий, чтобы опре­де­лить, какая из ко­манд начнёт игру с мячом. Ко­ман­да «Ста­тор» по оче­ре­ди иг­ра­ет с ко­ман­да­ми «Ротор», «Мотор» и «Стар­тер». Най­ди­те ве­ро­ят­ность того, что «Ста­тор» будет на­чи­нать толь­ко первую и по­след­нюю игры.

Ре­ше­ние. Тре­бу­ет­ся найти ве­ро­ят­ность про­из­ве­де­ния трех со­бы­тий: «Ста­тор» на­чи­на­ет первую игру, не на­чи­на­ет вто­рую игру, на­чи­на­ет тре­тью игру. Ве­ро­ят­ность про­из­ве­де­ния не­за­ви­си­мых со­бы­тий равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий. Ве­ро­ят­ность каж­до­го из них равна 0,5, от­ку­да на­хо­дим: 0,5·0,5·0,5 = 0,125.

Ответ: 0,125.

№ 28. Всем па­ци­ен­там с по­до­зре­ни­ем на ге­па­тит де­ла­ют ана­лиз крови. Если ана­лиз вы­яв­ля­ет ге­па­тит, то ре­зуль­тат ана­ли­за на­зы­ва­ет­ся по­ло­жи­тель­ным. У боль­ных ге­па­ти­том па­ци­ен­тов ана­лиз даёт по­ло­жи­тель­ный ре­зуль­тат с ве­ро­ят­но­стью 0,9. Если па­ци­ент не болен ге­па­ти­том, то ана­лиз может дать лож­ный по­ло­жи­тель­ный ре­зуль­тат с ве­ро­ят­но­стью 0,01. Из­вест­но, что 5% па­ци­ен­тов, по­сту­па­ю­щих с по­до­зре­ни­ем на ге­па­тит, дей­стви­тель­но боль­ны ге­па­ти­том. Най­ди­те ве­ро­ят­ность того, что ре­зуль­тат ана­ли­за у па­ци­ен­та, по­сту­пив­ше­го в кли­ни­ку с по­до­зре­ни­ем на ге­па­тит, будет по­ло­жи­тель­ным.

Ре­ше­ние. Ана­лиз па­ци­ен­та может быть по­ло­жи­тель­ным по двум при­чи­нам: А) па­ци­ент бо­ле­ет ге­па­ти­том, его ана­лиз верен; B) па­ци­ент не бо­ле­ет ге­па­ти­том, его ана­лиз ложен. Это не­сов­мест­ные со­бы­тия, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий. Имеем: 0,9*0,5+0,01*0,95=0,0545

Ответ: 0,0545.

№ 29. Ав­то­ма­ти­че­ская линия из­го­тав­ли­ва­ет ба­та­рей­ки. Ве­ро­ят­ность того, что го­то­вая ба­та­рей­ка не­ис­прав­на, равна 0,02. Перед упа­ков­кой каж­дая ба­та­рей­ка про­хо­дит си­сте­му кон­тро­ля. Ве­ро­ят­ность того, что си­сте­ма за­бра­ку­ет не­ис­прав­ную ба­та­рей­ку, равна 0,99. Ве­ро­ят­ность того, что си­сте­ма по ошиб­ке за­бра­ку­ет ис­прав­ную ба­та­рей­ку, равна 0,01. Най­ди­те ве­ро­ят­ность того, что слу­чай­но вы­бран­ная ба­та­рей­ка будет за­бра­ко­ва­на си­сте­мой кон­тро­ля.

Ре­ше­ние. Си­ту­а­ция, при ко­то­рой ба­та­рей­ка будет за­бра­ко­ва­на, может сло­жить­ся в ре­зуль­та­те со­бы­тий: A = ба­та­рей­ка дей­стви­тель­но не­ис­прав­на и за­бра­ко­ва­на спра­вед­ли­во или В = ба­та­рей­ка ис­прав­на, но по ошиб­ке за­бра­ко­ва­на. Это не­сов­мест­ные со­бы­тия, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей эти со­бы­тий. Имеем: 0,02 * 0,99 + 0,98 * 0,01 = 0,0296

Ответ: 0,0296.

№ 30. В кар­ма­не у Пети было 2 мо­не­ты по 5 руб­лей и 4 мо­не­ты по 10 руб­лей. Петя, не глядя, пе­ре­ло­жил какие-то 3 мо­не­ты в дру­гой кар­ман. Най­ди­те ве­ро­ят­ность того, что пя­ти­руб­ле­вые мо­не­ты лежат те­перь в раз­ных кар­ма­нах.

Ре­ше­ние. Чтобы пя­ти­руб­ле­вые мо­не­ты ока­за­лись в раз­ных кар­ма­нах, Петя дол­жен взять из кар­ма­на одну пя­ти­руб­ле­вую и две де­ся­ти­руб­ле­вые мо­не­ты. Это можно сде­лать тремя спо­со­ба­ми: 5, 10, 10; 10, 5, 10 или 10, 10, 5. Эти со­бы­тия не­сов­мест­ные, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий: (2/6*4/5*3/4) * 3 = 0,2 * 3 = 0,6

№ 31. Стре­лок стре­ля­ет по ми­ше­ни один раз. В слу­чае про­ма­ха стре­лок де­ла­ет вто­рой вы­стрел по той же ми­ше­ни. Ве­ро­ят­ность по­пасть в ми­шень при одном вы­стре­ле равна 0,7. Най­ди­те ве­ро­ят­ность того, что ми­шень будет по­ра­же­на (либо пер­вым, либо вто­рым вы­стре­лом).

Ре­ше­ние. Пусть A — со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на стрел­ком с пер­во­го вы­стре­ла, B — со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на со вто­ро­го вы­стре­ла. Ве­ро­ят­ность со­бы­тия A равна P (A) = 0,7. Со­бы­тие B на­сту­па­ет, если, стре­ляя пер­вый раз, стре­лок про­мах­нул­ся, а, стре­ляя вто­рой раз, попал. Это не­за­ви­си­мые со­бы­тия, их ве­ро­ят­ность равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий: P (B) = 0,3·0,7 = 0,21. Со­бы­тия A и B не­сов­мест­ные, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий:

P (A + B) = P (A) + P (B) = 0,7 + 0,21 = 0,91.

Ответ: 0,91.