Раздел IV. Элементы теории вероятностей в социологических исследованиях.
Лекция 1 Элементы комбинаторики
Цель:
1. Познакомить с основными принципами комбинаторики;
2. Изучить перестановки, размещения, сочетания;
3. Научить использовать элементы комбинаторики в социологических исследованиях.
План:
1. Основные принципы комбинаторики.
2. Перестановки.
3. Размещения.
4. Сочетания.
5. Использование элементов комбинаторики для обработки и анализа социологических данных.
Основные принципы комбинаторики.
Задачи, при решении которых приходится составлять различные комбинации из конечного числа элементов и производить подсчет числа всех возможных таких комбинаций, относятся к разделу математики, который называется комбинаторикой. Этот раздел математики находит широкое применение в социологии.
Важнейшими принципами комбинаторики являются принцип произведения и принцип сложения.
Принцип произведения. Если некоторый объект А может быть выбран из некоторого множества объектов  способами, а другой объект В может быть выбран
способами, а другой объект В может быть выбран  способами, то одновременный выбор объектов А и В можно осуществить (
способами, то одновременный выбор объектов А и В можно осуществить ( ×
×  ) способами.
) способами.
Пример 1. В турпоходе участвуют 18 первокурсников и 12 второкурсников. Каким количеством способов можно выбрать группу дежурных, где один первокурсник и один второкурсник.
Решение. Одного первокурсника можно выбрать  =18 способами, а одного второкурсника
=18 способами, а одного второкурсника  способами, тогда по принципу произведения группу дежурных можно выбрать
способами, тогда по принципу произведения группу дежурных можно выбрать  ×
×  =18*12=216 способами.
=18*12=216 способами.
Принцип сложения. Если некоторый объект А может быть выбран из некоторого множества объектов  способами, а другой объект В, отличный от А может быть выбран
способами, а другой объект В, отличный от А может быть выбран  способами, то выбрать либо А, либо В можно (
способами, то выбрать либо А, либо В можно ( +
+  ) способами.
) способами.
Пример 2. На полке в библиотеке стоят 5 книг по социальной психологии, 20 книг по социологии труда и 15 книг по статистике. Сколькими способами студент может выбрать одну книгу?
Решение. Книгу по социальной психологии студент может выбрать 5 способами, книгу по социологии труда - 20 способами, а книгу по статистике - 15 способами, тогда по принципу сложения одну книгу можно выбрать 5+20+15=40 способами.
Определение 1. Конечное или счетное множество (совокупность элементов) называется упорядоченным, если каждому элементу сопоставлен его порядковый номер, т.е. номер места, на котором он расположен. Упорядоченное множество образуют 33 буквы русского алфавита; множество студентов группы, если за порядок принять список журнала, и т. п. Упорядоченным бесконечным множеством является множество натуральных чисел.
Перестановки.
Определение 2. Множества элементов, состоящие из одних и тех же различных элементов и отличающиеся друг от друга только их порядком, называются перестановками этих элементов. Число всевозможных перестановок из n элементов обозначается  .
.
Например, во множестве из одного элемента существует одна перестановка, во множестве из двух элементов – две. В самом деле, обозначив элементы этого множества через a и b, мы можем составить две перестановки a; b и b; a. Во множестве из трех элементов  можно образовать 6 перестановок:
можно образовать 6 перестановок:
a; b; c, a; c; b, c; a; b, c; b; a, b; c; a, b; a; c.
Мы установили, в частности, что 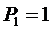 ,
,  ,
,  .
.
Число всевозможных перестановок из n элементов равно  (читается n факториал):
(читается n факториал):
 . (1)
. (1)
Замечание 1. Для пустого множества принимается соглашение: пустое множество можно упорядочить только одним способом; по определению полагают  .
.
Пример 3. Пусть в некоторое учреждение прибыли 6 психологов и их нужно закрепить за 6 группами трудных подростков. Сколько существует способов такого закрепления?
Решение. У первого психолога имеется 6 возможностей выбрать группу, у второго – уже только 5 возможностей, у третьего – 4 возможности, у четвертого – 3, у пятого – 2 и, наконец, у шестого – только одна возможность. Всего способов
 .
.
Пример 4. Сколькими различными маршрутами можно разнести корреспонденцию в 5 адресов?
Решение. Занумеруем адреса цифрами от 1 до 5. Каждому маршруту можно сопоставить один из наборов, состоящий из этих пяти цифр, например, (2,5,1,3,4). Всего различных маршрутов, т.е. отличающихся порядком наборов пяти цифр будет  .
.
Число перестановок с повторениями находится по формуле:
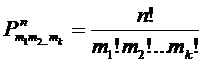 , где
, где 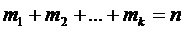 .
.
Размещения.
Каждая перестановка, составленная из элементов взятого множества, содержит все элементы этого множества. Но может оказаться, что из числа n элементов необходимо выбрать только определенное число m ( ) элементов, т. е возникает необходимость установить: сколько упорядоченных подмножеств по m элементов в каждом можно образовать из n элементов исходного множества.
) элементов, т. е возникает необходимость установить: сколько упорядоченных подмножеств по m элементов в каждом можно образовать из n элементов исходного множества.
Определение 3. Размещениями называются множества, состоящие из n различных элементов по m элементов, которые отличаются друг от друга либо составом элементов, либо их порядком (или и тем и другим). Количество всех возможных размещений из n элементов по m обозначается  .
.
Пример 5. Запишите все размещения из 3 элементов множества  по 2.
по 2.
Решение. Размещения будут следующие: ab, ac, bc, ba, ca, cb. Получили 6 размещений.
Для любых натуральных чисел m и n, удовлетворяющих условию  число размещений из n элементов по m элементов определяется формулами:
число размещений из n элементов по m элементов определяется формулами:
 ,
, 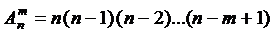
Замечание 2. По определению будем считать, что  .
.
Замечание 3. Так как перестановки можно считать частным случаем размещений при  , то
, то

Пример 6. Студентам - социологам надо сдать 4 экзамена за 8 дней. Сколькими способами можно составить расписание сдачи экзаменов?
Решение. Занумеруем дни сдачи экзаменов цифрами 1,2,…,8. Сначала выберем дни для сдачи экзаменов, например, (2,4,6,8), а затем порядок сдачи экзаменов. Таким образом, нужно составить различные наборы четырех чисел из восьми, которые отличаются друг от друга не только элементами, но и порядком их следования. Таких наборов  .
.
Пример 7. Перед выпуском группа студентов - социологов, состоящая из 19 человек, обменялась фотографиями. Сколько всего фотографий было роздано?
Решение. Группа студентов - социологов составляет множество элементов, участвовавших в обмене фотографиями, следовательно,  . Каждое размещение есть передача фотографии одним студентом другому. Поэтому
. Каждое размещение есть передача фотографии одним студентом другому. Поэтому  . Таким образом, всех фотографий было
. Таким образом, всех фотографий было  .
.
Пример 8. В конкурсе участвовало 10 фирм, трем из которых жюри должно присудить 1-е, 2-е и 3-е места. Сколько вариантов решения жюри существует?
Решение. В данном случае надо рассматривать размещения их 10 элементов по 3. Значит, количество вариантов равно
 .
.
Число размещений с повторениями: 
 .
.
Сочетания.
Определение 4. Сочетаниями из n различных элементов по m элементов называются множества, содержащие m элементов из числа n заданных, и которые отличаются друг от друга хотя бы одним элементом. Число всех сочетаний из n элементов по m обозначается  .
.
Пример 9. Запишите все сочетания из 3 элементов множества  по 2.
по 2.
Решение. Размещения будут следующие: ab, ac и bc. Заметим, что подмножества ab и ba совпадают. Получили 3 сочетания.
Число всех сочетаний из n элементов по m равно:
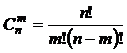
Замечание 4. При  величина
величина  .
.
Замечание 5. Условимся считать, что  при всех n.
при всех n.
Замечание 6. Кроме того, полезно знать, при  удобно применять формулу:
удобно применять формулу: 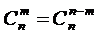 .
.
Число сочетаний с повторениями:
 .
.
Пример 10. Для проведения социологического опроса социологу необходимо выбрать 4 группы студентов выпускных курсов, имеющих гуманитарное направление обучения. Он подобрал 8 одинаково подходящих групп. Сколько существует способов отбора 4 группы из 8 в случайном порядке?
Решение. Так как всего найдено 8 групп, то  . Выбрать надо лишь 4, значит
. Выбрать надо лишь 4, значит 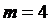 . Так как порядок групп в отборе значения не имеет, то необходимо определить число сочетаний из 8 по 4:
. Так как порядок групп в отборе значения не имеет, то необходимо определить число сочетаний из 8 по 4:
 .
.
Пример 11. В хоккейном турнире участвуют 10 команд. Каждая команда должна сыграть с каждой одну игру. Сколько игр сыграно в турнире?
Решение. Так как порядок среди двух команд, играющих в одной игре, не имеет значения, то различные пары команд образуют сочетания из 10 команд по две. Число игр, сыгранных в турнире, будет равно
 .
.
Использование элементов комбинаторики для обработки и анализа социологических данных.
Рассмотрим вопрос о том, с кем респондент проводит или предпочитает проводить свое свободное время.
| 1. С друзьями |
| 2. С коллегами по работе, учебе |
| 3. С членами своей семьи |
| 4. С другими родственниками |
| 5. В одиночестве |
| 6. С любимым человеком |
Респонденту обычно предлагается один из следующих способов ответа:
1) проранжировать, т.е. упорядочить (например, по важности) позиции;
2) отметить заданное число позиций (например, 3 позиции);
3) отметить заданное число позиций (например, 3 позиции) и проранжировать их;
4) отметить не больше заданного числа позиций;
5) отметить любое число позиций.
Нас интересует, сколькими вариантами можно ответить на такой вопрос при каждом способе ответа? Этот вопрос важен, в частности, при статистической обработке данных анкеты.
Переведем эти вопросы на математический язык. Пусть имеется множество 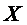 , состоящее из
, состоящее из 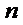 элементов (в нашем случае из 7) требуется:
элементов (в нашем случае из 7) требуется:
1)упорядочить это множество, т.е. вычислить  ,
, 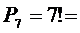 720*7=.
720*7=.
2)выбрать из него подмножество из  элементов, где
элементов, где  - заданное число (разумеется,
- заданное число (разумеется,  ) а это
) а это  , в нашем случае m=3
, в нашем случае m=3 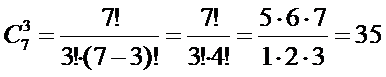 .
.
3)выбрать подмножество из  элементов и упорядочить его, а это
элементов и упорядочить его, а это  , в нашем случае m=3
, в нашем случае m=3  .
.
4)выбрать из 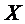 подмножество не более чем из
подмножество не более чем из 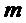 элементов, для этого нужно вычислить
элементов, для этого нужно вычислить  , при этом слагаемое
, при этом слагаемое 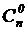 учитывает случай, когда выбирается пустое множество или, применительно к ответам на вопрос анкеты, когда респондент не отмечает ни одной позиции, в нашем случае
учитывает случай, когда выбирается пустое множество или, применительно к ответам на вопрос анкеты, когда респондент не отмечает ни одной позиции, в нашем случае  .
.
5)выбрать из  произвольное подмножество, т.е. нужно вычислить число всевозможных подмножеств множества
произвольное подмножество, т.е. нужно вычислить число всевозможных подмножеств множества 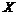 , т.е. вычислить мощность множества всех подмножеств множества
, т.е. вычислить мощность множества всех подмножеств множества 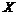
 а мощность этого множества равна
а мощность этого множества равна  , в нашем случае
, в нашем случае 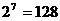 .
.