Примем некоторые допущения относительно уравнения:
yt=a0+a1xt+ εt (8)
• пусть yt и xt не содержат тенденции, например, представляют собой отклонения выровненных по трендам значений от исходных уровней временных рядов;
• пусть оценки а0 и а1 параметров уравнения регрессии найдены обычным МНК;
• пусть критерий Дарбина-Уотсона показал наличие автокорреляции в остатках первого порядка.
Чтобы понять, каковы последствия автокорреляции в остатках для оценок параметров модели регрессии, найденных обычным МНК, построим формальную модель, описывающую автокорреляцию в остатках. Автокорреляция в остатках первого порядка предполагает, что каждый следующий уровень остатков εt зависит от предыдущего уровня εt -1.
Следовательно, существует модель регрессии вида
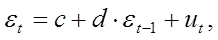 (9)
(9)
где с и d – параметры уравнения регрессии.
В соответствий с рабочими формулами МНК имеем:
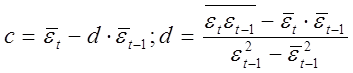 (10)
(10)
Учитывая, что сумма остатков равна нулю можно показать, что:
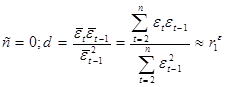 (11)
(11)
где 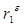 – коэффициент автокорреляции остатков первого порядка.
– коэффициент автокорреляции остатков первого порядка.
Таким образом, имеем:
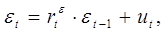 (12)
(12)
где ut – случайная ошибка.
Заметим, что | 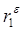 | < 1.
| < 1.
Учитывая соотношение (12), уравнение (8) можно переписать в виде
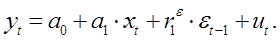 (13)
(13)
Найденные соотношения показывают, что текущий уровень ряда yt зависит не только от факторной переменной xt, но и от остатков предшествующего периода 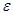 t-1.
t-1.
Допустим, мы не принимаем во внимание эту информацию и определяем оценки параметров а0 и а1 уравнения (8) обычным МНК. Тогда можно показать, что полученные оценки неэффективны, т. е. они не имеют минимальную дисперсию. Это приводит к увеличению стандартных ошибок, снижению фактических значений t- критерия и широким доверительным интервалам для коэффициента регрессии. На основе таких результатов можно сделать ошибочный вывод о незначимом влиянии исследуемою фактора на результат, в то время как на самом деле его влияние статистически значимо.
При соблюдении прочих предпосылок МНК автокорреляция остатков не влияет на свойства состоятельности и несмещенности оценок параметров уравнения регрессии обычным МНК, за исключением моделей авторегрессии. Применение МНК к моделям авторегрессии ведет к получению смещенных, несостоятельных и неэффективных оценок.
Итак, если остатки по исходному уравнению регрессии содержат автокорреляцию, то для оценки параметров уравнения используют обобщенный МНК. Для его реализации необходимо выполнять следующие условия.
1. Преобразовать исходные переменные уt, и хt, к виду 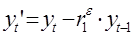 и
и 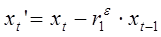 .
.
2. Применив обычный МНК к уравнению 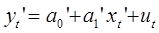 , определить оценки параметров
, определить оценки параметров 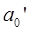 и
и 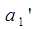 .
.
3. Рассчитать параметр а исходного уравнения из соотношения 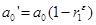 t по формуле:
t по формуле:
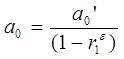 (14)
(14)
4. Выписать исходное уравнение (8).
Обобщенный метод наименьших квадратов аналогичен методу последовательных разностей. Однако мы вычитаем из уt не все значения предыдущего уровня yt-1, а некоторую его долю 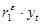 . При
. При 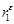 =1 это будут первые разности
=1 это будут первые разности 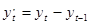 и
и 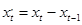 .
.
Поэтому в случае, если значение критерия Дарбина-Уотсона близко к нулю, применение метода первых разностей вполне обоснованно. Если 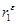 = –1, т. е. в остатках наблюдается полная отрицательная автокорреляция, то изложенный выше метод заменяется моделью:
= –1, т. е. в остатках наблюдается полная отрицательная автокорреляция, то изложенный выше метод заменяется моделью:
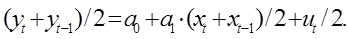 (15)
(15)
В этой модели определяют средние за два периода уровни каждого ряда, а затем по полученным усредненным уровням обычным МНК рассчитываем параметры a0 и a1. Данная модель называется моделью регрессии по скользящим средним.
Основная проблема, связанная с применением данного метода, заключается в том, как получить оценку 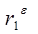
Существует множество способов оценить численное значение коэффициента автокорреляции остатков первого порядка. Однако основными способами являются оценка этого коэффициента непосредственно по остаткам, полученным по исходному уравнению регрессии, и получение его приближенного значения из соотношения между коэффициентом автокорреляции остатков первого порядка и критерием Дарбина-Уотсона: 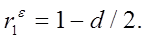
ПРИЛОЖЕНИЕ А
Таблица
| Статистика Дарбина-Уотсона: dL и dU (уровень значимости 5%) | ||||||||||
| n | k=1 | k=2 | k=3 | k=4 | k=5 | |||||
| d L | d U | d L | d U | d L | d U | d L | d U | d L | d U | |
| 0,70 | 1,36 | 0,95 | 1,54 | 0,82 | 1,75 | 0,69 | 1,97 | 0,56 | 2,21 | |
| 1,10 | 1,37 | 0,98 | 1,54 | 0,86 | 1,73 | 0,74 | 1,93 | 0,62 | 2,15 | |
| 1,13 | 1,38 | 1,02 | 1,54 | 0,90 | 1,71 | 0,78 | 1,90 | 0,67 | 2,10 | |
| 1,16 | 1,39 | 1,05 | 1,53 | 0,93 | 1,69 | 0,82 | 1,87 | 0,71 | 2,06 | |
| 1,18 | 1,40 | 1,08 | 1,53 | 0,97 | 1,68 | 0,86 | 1,85 | 0,75 | 2,02 | |
| 1,20 | 1,41 | 1,10 | 1,54 | 1,00 | 1,68 | 0,90 | 1,83 | 0,79 | 1,99 | |
| 1,22 | 1,42 | 1,13 | 1,54 | 1,03 | 1,67 | 0,93 | 1,81 | 0,83 | 1,96 | |
| 1,24 | 1,43 | 1,15 | 1,54 | 1,05 | 1,66 | 0,96 | 1,80 | 0,86 | 1,94 | |
| 1,26 | 1,44 | 1,17 | 1,54 | 1,08 | 1,66 | 0,99 | 1,79 | 0,90 | 1,92 | |
| 1,27 | 1,45 | 1,19 | 1,55 | 1,10 | 1,66 | 1,01 | 1,78 | 0,93 | 1,90 | |
| 1,29 | 1,45 | 1,21 | 1,55 | 1,12 | 1,66 | 1,04 | 1,77 | 0,95 | 1,89 | |
| 1,30 | 1,46 | 1,22 | 1,55 | 1,14 | 1,65 | 1,06 | 1,76 | 0,98 | 1,88 | |
| 1,32 | 1,47 | 1,24 | 1,56 | 1,16 | 1,65 | 1,08 | 1,76 | 1,01 | 1,86 | |
| 1,33 | 1,48 | ,26 | 1,56 | 1,18 | 1,65 | 1,10 | 1,75 | 1,03 | 1,85 | |
| 1,34 | 1,48 | 1,27 | 1,56 | 1,20 | 1,65 | 1,12 | 1,74 | 1,05 | 1,84 | |
| 1,35 | 1,49 | 1,28 | 1,57 | 1,21 | 1,65 | 1,14 | 1,74 | 1,07 | 1,83 | |
| 1,36 | 1,50 | 1,30 | 1,57 | 1,23 | 1,65 | 1,16 | 1,74 | 1,09 | 1,83 | |
| 1,37 | 1,50 | 1,31 | 1,57 | 1,24 | 1,65 | 1,18 | 1, 73 | 1,11 | 1,82 | |
| 1,38 | 1,51 | 1,32 | 1,58 | 1,26 | 1,65 | 1,19 | 1,73 | 1,13 | 1,81 | |
| 1,39 | 1,51 | 1,33 | 1,58 | 1,27 | 1,65 | 1,21 | 1,73 | 1,15 | 1,81 | |
| 1,40 | 1,52 | 1,34 | 1,58 | 1,28 | 1,65 | 1,22 | 1,73 | 1,16 | 1,80 | |
| 1,41 | 1,52 | 1,35 | 1,59 | 1,29 | 1,65 | 1,24 | 1,73 | 1,18 | 1,80 | |
| 1,42 | 1,53 | 1,36 | 1,59 | 1,31 | 1,66 | 1,25 | 1,72 | 1,19 | 1,80 | |
| 1,43 | 1,54 | 1,37 | 1,59 | 1,32 | 1,66 | 1,26 | 1,72 | 1,21 | 1,79 | |
| 1,43 | 1,54 | 1,38 | 1,60 | 1,33 | 1,66 | 1,27 | 1,72 | 1,22 | 1,79 | |
| 1,44 | 1,54 | 1,39 | 1,60 | 1,34 | 1,66 | 1,29 | 1,72 | 1,23 | 1,79 | |
| 1,48 | 1,57 | 1,43 | 1,62 | 1,38 | 1,67 | 1,34 | 1,72 | 1,29 | 1,78 | |
| 1,50 | 1,59 | 1,46 | 1,63 | 1,42 | 1,67 | 1,38 | 1,72 | 1,34 | 1,77 | |
| 1,53 | 1,60 | 1,49 | 1,64 | 1,45 | 1,68 | 1,41 | 1,72 | 1,38 | 1,77 | |
| 1,55 | 1,62 | 1,51 | 1,65 | 1,48 | 1,69 | 1,44 | 1,73 | 1,41 | 1,77 | |
| 1,57 | 1,63 | 1,54 | 1,66 | 1,50 | 1,70 | 1,47 | 1,73 | 1,44 | 1,77 | |
| 1,58 | 1,64 | 1,55 | 1,67 | 1,52 | 1,70 | 1,49 | 1,74 | 1,46 | 1,77 | |
| 1,60 | 1,65 | 1,57 | 1,68 | 1,54 | 1,71 | 1,51 | 1,74 | 1,49 | 1,77 | |
| 1,61 | 1,66 | 1,59 | 1,69 | 1,56 | 1,72 | 1,53 | 1,74 | 1,51 | 1,77 | |
| 1,62 | 1,67 | 1,60 | 1,70 | 1,57 | 1,72 | 1,55 | 1,75 | 1,52 | 1,77 | |
| 1,63 | 1,68 | 1,61 | 1,70 | 1,59 | 1,73 | 1,57 | 1,75 | 1,54 | 1,78 | |
| 1,64 | 1,69 | 1,62 | 1,71 | 1,60 | 1,73 | 1,58 | 1,75 | 1,56 | 1,78 | |
| 1,65 | 1,69 | 1,63 | 1,72 | 1,61 | 1,74 | 1,59 | 1,76 | 1,57 | 1,78 |
Окончание табл.
| Статистика Дарбина-Уотсона: dL и dU (уровень значимости 5%) | ||||||||||
| n | k=1 | k=2 | k=3 | k=4 | k=5 | |||||
| d L | d U | d L | d U | d L | d U | d L | d U | d L | d U | |
| 0,81 | 1,07 | 0,70 | 1,25 | 0,59 | 1,46 | 0,49 | 1,70 | 0,39 | 1,96 | |
| 0,84 | 1,09 | 0,74 | 1,25 | 0,63 | 1,44 | 0,53 | 1,66 | 0,44 | 1,90 | |
| 0,87 | 1,10 | 0,77 | 1,25 | 0,67 | 1,43 | 0,57 | 1,63 | 0,48 | 1,85 | |
| 0,90 | 1,12 | 0,80 | 1,26 | 0,71 | 1,42 | 0,61 | 1,60 | 0,52 | 1,80 | |
| 0,93 | 1,13 | 0,83 | 1,26 | 0,74 | 1,41 | 0,65 | 1,58 | 0,56 | 1,77 | |
| 0,95 | 1,15 | 0,86 | 1,27 | 0,77 | 1,41 | 0,68 | 1,57 | 0,60 | 1,74 | |
| 0,97 | 1,16 | 0,89 | 1,27 | 0,80 | 1,41 | 0,72 | 1,55 | 0,63 | 1,71 | |
| 1,00 | 1,17 | 0,91 | 1,28 | 0,83 | 1,40 | 0,75 | 1,54 | 0,66 | 1,69 | |
| 1,02 | 1,19 | 0,94 | 1,29 | 0,86 | 1,40 | 0,77 | 1,53 | 0,70 | 1,67 | |
| 1,04 | 1,20 | 0,96 | 1,30 | 0,88 | 1,41 | 0,80 | 1,53 | 0,72 | 1,66 | |
| 1,05 | 1,21 | 0,98 | 1,30 | 0,90 | 1,41 | 0,83 | 1,52 | 0,75 | 1,65 | |
| 1,07 | 1,22 | 1,00 | 1,31 | 0,93 | 1,41 | 0,85 | 1,52 | 0,78 | 1,64 | |
| 1,09 | 1,23 | 1,02 | 1,32 | 0,95 | 1,41 | 0,88 | 1,51 | 0,81 | 1,63 | |
| 1.10 | 1,24 | 1,04 | 1,32 | 0,97 | 1,41 | 0,90 | 1,51 | 0,83 | 1,62 | |
| 1,12 | 1,25 | 1,05 | 1,33 | 0,99 | 1,42 | 0,92 | 1,51 | 0,85 | 1,61 | |
| 1,13 | 1,26 | 1,07 | 1,34 | 1,01 | 1,42 | 0,94 | 1,51 | 0,88 | 1,61 | |
| 1,15 | 1,27 | 1,08 | 1,34 | 1,02 | 1,42 | 0,96 | 1,51 | 0.90 | 1,60 | |
| 1,16 | 1,28 | 1,10 | 1,35 | 1,04 | 1,43 | 0,98 | 1,51 | 0,92 | 1,60 | |
| 1,17 | 1,29 | 1,11 | 1,36 | 1,05 | 1,43 | 1,00 | 1,51 | 0,94 | 1,59 | |
| 1,18 | 1,30 | 1,13 | 1,36 | 1,07 | 1,43 | 1,01 | 1,51 | 0,95 | 1,59 | |
| 1,19 | 1,31 | 1,14 | 1,37 | 1,08 | 1,44 | 1,03 | 1,51 | 0,97 | 1,59 | |
| 1,21 | 1,32 | 1,15 | 1,38 | 1,10 | 1,44 | 1,04 | 1,51 | 0,99 | 1,59 | |
| 1,22 | 1,32 | 1,16 | 1,38 | 1,11 | 1,45 | 1,06 | 1,51 | 1,00 | 1,59 | |
| 1,23 | 1,33 | 1,18 | 1,39 | 1,12 | 1,45 | 1,07 | 1,52 | 1,02 | 1,58 | |
| 1,24 | 1,34 | 1,19 | 1,39 | 1,14 | 1,45 | 1,09 | 1,52 | 1,03 | 1,58 | |
| 1,25 | 1,34 | 1,20 | 1,40 | 1,15 | 1,46 | 1,10 | 1,52 | 1,05 | 1,58 | |
| 1,29 | 1,38 | 1,24 | 1,42 | 1,20 | 1,48 | 1,16 | 1,53 | 1,11 | 1,58 | |
| 1,32 | 1,40 | 1,28 | 1,45 | 1,24 | 1,49 | 1,20 | 1,54 | 1,16 | 1,59 | |
| 1,36 | 1,43 | 1,32 | 1,47 | 1,28 | 1,51 | 1,25 | 1,55 | 1,21 | 1,59 | |
| 1,38 | 1,45 | 1,35 | 1,48 | 1,32 | 1,52 | 1,28 | 1,56 | 1,25 | 1,60 | |
| 1,41 | 1,47 | 1,38 | 1,50 | 1,35 | 1,53 | 1,31 | 1,57 | 1,28 | 1,61 | |
| 1,43 | 1,49 | 1,40 | 1,52 | 1,37 | 1,55 | 1,34 | 1,58 | 1,31 | 1,61 | |
| 1,45 | 1,50 | 1,42 | 1,53 | 1,39 | 1,56 | 1,37 | 1,59 | 1,34 | 1,62 | |
| 1,47 | 1,52 | 1,44 | 1,54 | 1,42 | 1,57 | 1,39 | 1,60 | 1,36 | 1,62 | |
| 1,48 | 1,53 | 1,46 | 1,55 | 1,43 | 1,58 | 1,41 | 1,60 | 1,39 | 1,63 | |
| 1,50 | 1,54 | 1,47 | 1,56 | 1,45 | 1,59 | 1,43 | 1,61 | 1,41 | 1,64 | |
| 1,51 | 1,55 | 1,49 | 1,57 | 1,47 | 1,60 | 1,45 | 1,62 | 1,42 | 1,64 | |
| 1,52 | 1,56 | 1,50 | 1,58 | 1,48 | 1,60 | 1,46 | 1,63 | 1,44 | 1,65 |