Рассмотрим тот же график 
и познакомимся с функцией переменной площади 
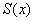. Что это за функция? Зафиксируем произвольную точку 
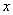(левая красная точка), лежащую между точками «а» и «бэ»:
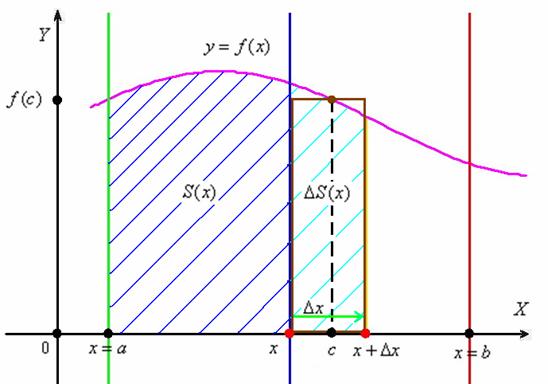
В данной точке функция 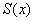равна площади криволинейной трапеции, которая расположена между зелёной и синей линиями и заштрихована синим цветом. Мысленно начните уменьшать значение «икс» и сдвигать синюю прямую влево – площадь 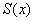начнёт уменьшаться и, в конце концов, в точке 
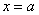станет равной нулю: 
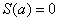(прямые совпадут). Теперь возвращаемся на исходную позицию и сдвигаем синюю линию вправо – в этом случае площадь 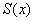начнёт расти. И когда мы достигнем верхнего предела 
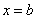(синяя прямая «закроет» красную), площадь будет равна в точности площади всей криволинейной трапеции: 
.
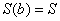Таким образом, аргумент может изменяться в пределах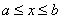 
, при этом функция 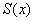(площадь) будет возрастать от 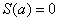до .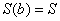
Докажем, что функция переменной площади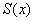является первообразной функцией для функции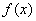, то есть докажем, что
.
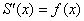Вернёмся к нашей точке «икс» и зададим в ней приращение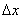 
(зелёная стрелка). Для определённости полагаем, что 
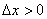(случай 
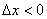доказывается аналогично). Приращение аргумента 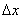влечёт приращение функции 
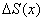– геометрически это площадь криволинейной трапеции, которая заштрихована голубым цветом.
По так называемой теореме о среднем, на отрезке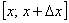 
существует точка «цэ» – такая, что площадь коричневого прямоугольника равна площади голубой трапеции:
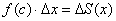
Примечание: этот участок чертежа схематичен, поскольку мне трудно подобрать идеально точное местоположение точки «цэ»
По определению производной, производная функции – это отношение приращения функции 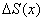к приращению аргумента 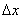при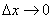 
:
.
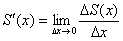И, ввиду равенства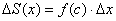 
:
|
|
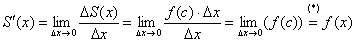
(*) Так как 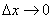, то точка «цэ» бесконечно близко приближается к точке «икс», и, соответственно: 
.
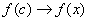Таким образом, для любого 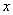из рассматриваемого промежутка справедливо равенство 
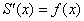, означающее, что функция 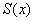является первообразной для функции .
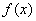По теореме, доказанной в самом начале урока, множество всех первообразных представимо в виде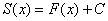 
(отличаются друг от друга константой).
Теперь в данное равенство подставляем 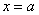и соответствующее значение площади :
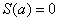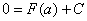, откуда следует, что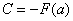 
Найденное значение константы 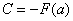подставляем в :
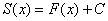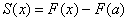
Выруливаем на финишную прямую. При 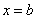функция 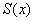принимает значение, равное площади всей криволинейной трапеции: 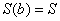. Подставим 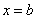и 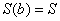в уравнение :
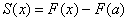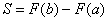
Следует отметить, что в учебниках по высшей математике вывод этой формулы проводится в более солидном ключе – с помощью интеграла с переменным верхним пределом. Я же ограничился упрощенной версией доказательства, чтобы материал был понятен бОльшему количеству читателей.
Это ещё, кстати, не всё =) Завершаем мысль:
В предыдущем параграфе мы доказали, что площадь криволинейной трапеции – есть предел интегральной суммы: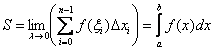 
.
Но с другой стороны, .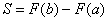
И из этих двух фактов следует лаконичная формула Ньютона-Лейбница:
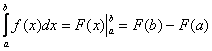, где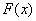 
– первообразная функция для функции .
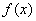Свойства определённого интеграла
У меня нет цели копипастить учебники, и я остановлюсь только на тех свойствах, которые имеют существенное значение для практики. Нумерация, пожалуй, ни к чему:
– Первое свойство: интеграл с одинаковыми пределами интегрирования равен нулю: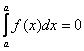 
. Графическая интерпретация очевидна: криволинейная трапеция вырождается в отрезок, а площадь отрезка с геометрической точки зрения равна нулю.
|
|
– Свойства линейности:
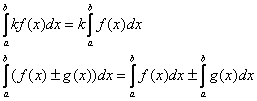
– Если у интеграла поменять местами пределы интегрирования, то он сменит знак:
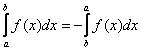
Почему? Пусть для определённости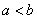 
. Тогда при перестановке пределов интегрирования разбиение отрезка 
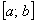будет проводиться справа налево (вспоминаем ступенчатую фигуру 1-го чертёжа), и длины частичных промежутков формально станут отрицательными 
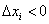, поэтому интегральная сумма 
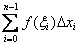и сам интеграл (как предел суммы) сменит знак.
– Какими бы ни были точки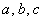 
:
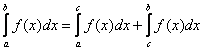
– Пожалуйста, запомните! Если подынтегральная функция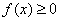 
, то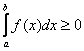 
(здесь и далее полагаем, что 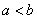). И, наоборот, если 
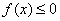, то интеграл будет неположительным: 
.
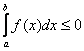! Совет: перед решением любого определённого интеграла всегда полезно проанализировать знак подынтегральной функции!
– Ещё одно важное свойство. Если функции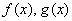 
интегрируемы на 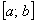, и для всех «икс» из данного промежутка справедливо неравенство 
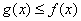, то
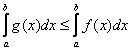
Из данного свойства следует важнейшая рабочая формула вычисления площади фигуры, ограниченной графиками функций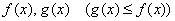 
и прямыми 
:
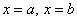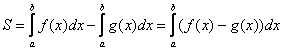
Если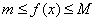 
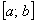на , то 