В пространстве даны сила 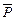 и ось
и ось  (рис. 3.6). Спроектируем силу на плоскость, перпендикулярную оси.
(рис. 3.6). Спроектируем силу на плоскость, перпендикулярную оси.
Плечом силы ( ) будем называть кратчайшее расстояние от точки О пересечения оси с плоскостью до проекции
) будем называть кратчайшее расстояние от точки О пересечения оси с плоскостью до проекции  силы
силы 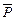 на плоскость.
на плоскость.
Моментом силы 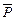 относительно оси
относительно оси  называется взятое со знаком плюс или минус произведение модуля проекции силы на плоскость, перпендикулярную оси, на плечо.
называется взятое со знаком плюс или минус произведение модуля проекции силы на плоскость, перпендикулярную оси, на плечо.
Обозначая момент силы относительно оси  через
через 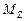 , напишем
, напишем  . Знак плюс берется в том случае, если наблюдателю, смотрящему на плоскость с положительного направления оси, проекция силы видна вращающейся вокруг оси в направлении, противоположном вращению часовой стрелки; знак минус берется, если это вращение видно в направлении вращения часовой стрелки.
. Знак плюс берется в том случае, если наблюдателю, смотрящему на плоскость с положительного направления оси, проекция силы видна вращающейся вокруг оси в направлении, противоположном вращению часовой стрелки; знак минус берется, если это вращение видно в направлении вращения часовой стрелки.

Рис. 3.6.
Из определения вытекает, что момент силы относительно оси равен нулю в двух случаях (предполагается, что сила отлична от нуля):
1) сила 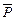 параллельна оси, так как тогда ее проекция на плоскость, перпендикулярную оси, равна нулю;
параллельна оси, так как тогда ее проекция на плоскость, перпендикулярную оси, равна нулю;
2) линия действия силы пересекает ось, так как в этом случае плечо  .
.
Если при записи момента силы относительно оси, необходимо указать название силы, то эту последнюю записывают в скобках.
Например, символ  означает момент силы
означает момент силы  относительно оси х,
относительно оси х,  - момент силы
- момент силы  относительно оси z и т.п.
относительно оси z и т.п.
Теорема Вариньона о моменте равнодействующей
Относительно оси
Дано твердое тело, на которое действует система сил  приводящая к равнодействующей
приводящая к равнодействующей 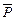 (рис.3.7).
(рис.3.7).

Рис. 3.7
Мысленно присоединим к телу вдоль линии действия 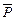 силу
силу  . Очевидно, что система сил
. Очевидно, что система сил  и
и  будет находиться в равновесии. Составим для этой новой системы сил уравнение моментов, беря моменты относительно оси Ох,
будет находиться в равновесии. Составим для этой новой системы сил уравнение моментов, беря моменты относительно оси Ох, 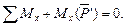 Так как
Так как 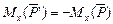 , то, или
, то, или  .
.
Эта формула выражает теорему Вариньона: если система сил приводится к равнодействующей, то момент этой равнодействующей, относительно какой-либо оси равен сумме моментов всех сил системы относительно этой же оси.
Методика решения задачи
Пример 3.1
Для данной пространственно расположенной конструкции (рис. 3.8) определить реакции связей, если на конструкцию действует: сила  ;
;  ;
;  ;
;  ;
; 

Рис. 3.8
Решение:
Проставим реакции связей данной конструкции: в точках А и В – подшипники, которые имеют реакции  в точке С – гладкая опор, ее реакция направлена перпендикулярно плоскости, на которой она находится, то есть
в точке С – гладкая опор, ее реакция направлена перпендикулярно плоскости, на которой она находится, то есть  (рис.3.9);
(рис.3.9);

Рис. 3. 9
2) составим уравнения равновесия данной конструкции:

 ;
;
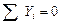 ;
;
 ;
;
 ;
;
 ;
;
 ;
;

 ;
;
 ;
;
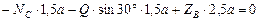 ;
;
 ;
;
 .
.
Составим уравнения:

 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Ответ:  ,
,  ,
,  ,
,  ,
,  .
.
Задачи для выполнения расчетно-графической работы
С-3. РАВНОВЕСИЕ ТВЁРДОГО ТЕЛА. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ОПОР
ПРОСТРАНСТВЕННОЙ КОНСТРУКЦИИ
Для заданной пространственно расположенной конструкции определить реакции опор. Варианты схем указанны на рисунке 3.10, нагрузки для схем в таблице 3.1.
Таблица 3.1
Исходные данные для задачи С-3
| вариант | I | II | III | ||||||
x
α1
y

|  z
α2
y z
α2
y
| z  α3
x
α3
x
| М, кН×м | а, м | b, м | ||||
| Т=20 кН | G=15 кН | Q=25 кН | |||||||
| Точка приложения | α1, град | Точка приложения | α2, град | Точка приложения | α3, град | ||||
| K | L | N | 0.3 | 0.6 | |||||
| L | N | K | 0.4 | 0.6 | |||||
| N | K | L | 0.5 | 0.6 | |||||
| K | L | N | 0.6 | 0.9 | |||||
| L | N | K | 0.7 | 0.9 | |||||
| N | K | L | 0.8 | 0.9 | |||||
| K | L | N | 0.9 | 1.2 | |||||
| L | N | K | 1.0 | 1.2 | |||||
| N | K | L | 1.0 | 1.2 | |||||
| K | L | N | 0.9 | 1.2 | |||||
| L | N | K | 0.8 | 0.9 | |||||
| N | K | L | 0.7 | 0.9 | |||||
| K | L | N | 0.6 | 0.9 | |||||
| L | N | K | 0.5 | 1.2 | |||||
| N | K | L | 0.3 | 1.2 | |||||
| K | L | N | 0.5 | 1.2 | |||||
| L | N | K | 0.6 | 0.6 | |||||
| N | K | L | 0.8 | 0.6 | |||||
Примечание: – для схем 1–12 АК=  , CN= , CN= 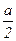 , CL= , CL=  – для схем 13–18 R= 3a, r=
– для схем 13–18 R= 3a, r= 
|
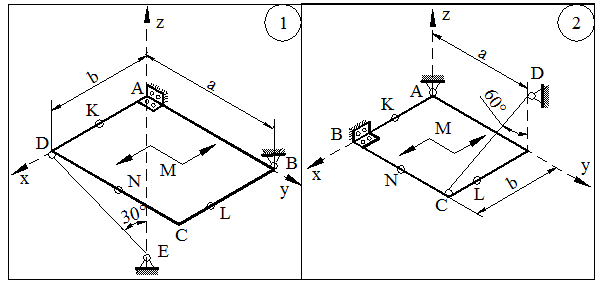

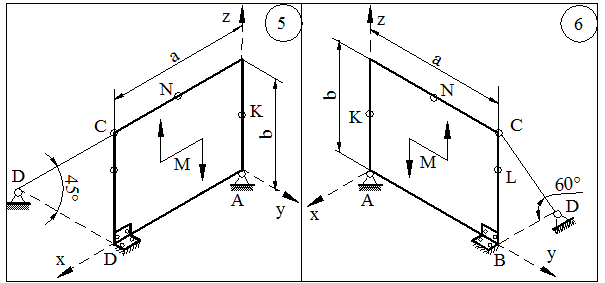
Рисунок 3.10



Рисунок 3.10 - продолжение



Рисунок 3.10 - окончание
Практическое занятие 4
Определение положения центра тяжести тела [1,2,5,6,7]