С-4. ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ ПЛАСТИНЫ
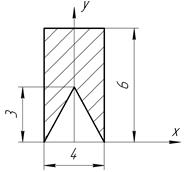
Определить координаты центра тяжести плоской фигуры, изображенной на чертеже (размеры в сантиметрах) рисунок 4.5 [7].
С-4, в.1
| С-4, в.2
|
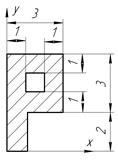
С-4, в.3
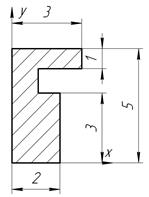
| С-4, в.4
|
С-4, в.5
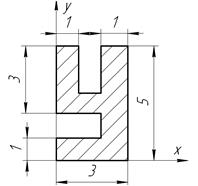Рис. 4.5
| С-4, в.6
|
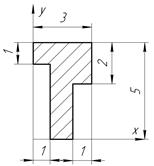
С-4, в.7
| С-4, в.8
|
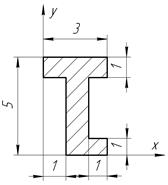
С-4, в.9
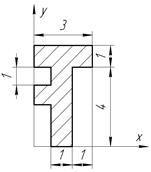
| С-4, в.10
|
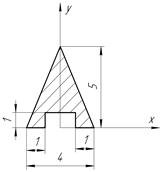
С-4, в.11
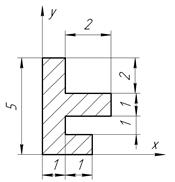
| С-4, в.12
|
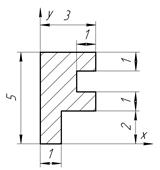
С-4, в.13
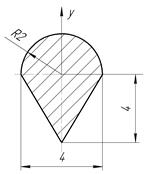
| С-4, в.14
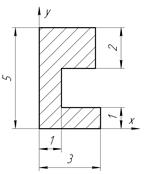Продолжение рис. 4.5
|
С-4, в.15
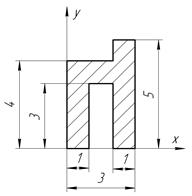
| С-4, в.16
|
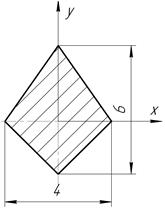
С-4, в.17
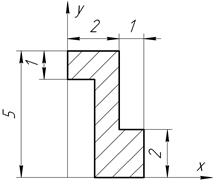
| С-4, в.18
|
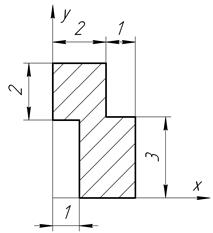
С-4, в.19
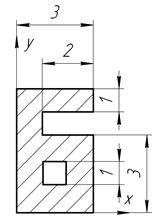
| С-4, в.20
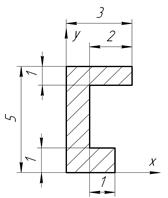Продолжение рис. 4.5
|
С-4, в.21
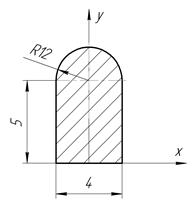
| С-4, в.22
|
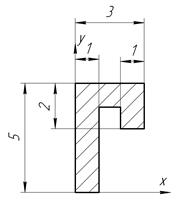
С-4, в.23
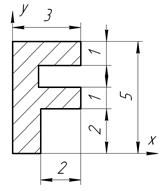
| С-4, в.24
|
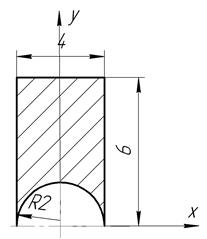
С-4, в.25
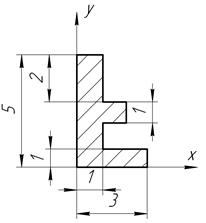
| С-4, в.26
|
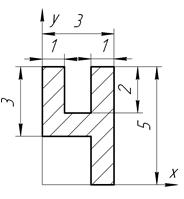
С-4, в.27
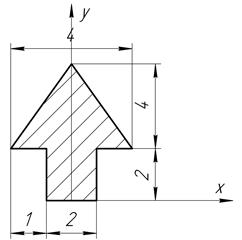
| Продолжение рис. 4.5
С-4, в.28
|
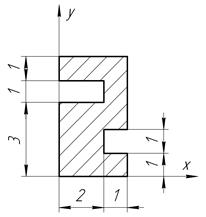
С-4, в.29
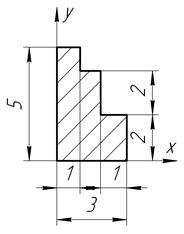
| С-4, в.30
|
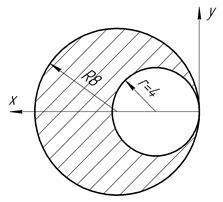
Окончание рис. 4.5
Практическое занятие 5
Определение скорости и ускорения точки по заданным уравнениям ее движения. Составление уравнений движения точки и определение ее скорости и ускорения
Кинематика точки. Поступательное движение.
Скорость и ускорение точки [1,2,3,4,5,6]
Определение траектории движения точки
Чтобы получить уравнение траектории движения точки, необходимо найти зависимость между координатами, исключив переменную t из уравнений координат, то есть x=f(y).
а) уравнение движения точки имеет вид: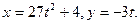 
Выразим из второго уравнения переменную t: t=-y/3 и подставим первое уравнение:
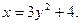
Получаем уравнение параболы.
б)необходимо воспользоваться соотношениями между тригонометрическими функциями, в случае x=12cos(πt/6), y=4sin(πt/6).
Возведем в квадрат обе части каждого из уравнений и сложим правые и левые части уравнений:
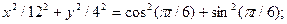
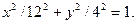
Получим уравнение эллипса.
в)подбор коэффициентов и математические преобразования:
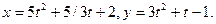
Умножим первое уравнение на 3, второе на 5, получим:
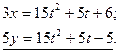
Вычтем из первого уравнения второе:
3 x-5y=11.
Получим уравнение прямой линии:
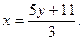
Определение скорости и ускорения точки
Скорость точки при поступательном движении определяется:
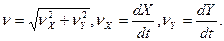
Вектор скорости направляется по касательной к траектории движения точки.
Ускорение точки определяется:
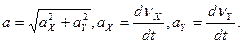
Нормальное ускорение точки: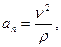 
где ρ – радиус кривизны траектории движения точки.
Нормальное (центростремительное) ускорение направляется от точки по радиусу кривизны к центру.
Тангенциальное ускорение определяется:
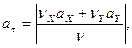
Тангенциальное (касательно) ускорение направляется по касательной к траектории движения точки.
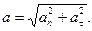
Направляется как результирующий вектор, построенный на нормальном и тангенциальном ускорениях точки (рис.5.1).
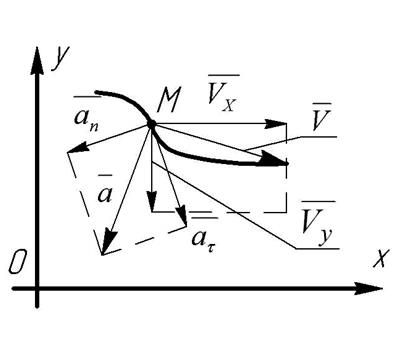
Рис.5.1
В случае поступательного прямолинейного движения точки:
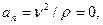
где ρ – радиус кривизны прямой (ρ=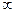 
).
Тогда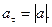 
Пример 5.1
Определить вид траектории движения точки, найти ее положение при 
, а также определить ее скорость, нормальное, тангенциальное, и полное ускорение, если 
, 
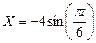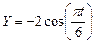-3.
Решение:
Определим вид траектории движения точки: исключив переменную из уравнений координат, найдем зависимость:
.
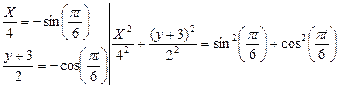Получаем уравнение эллипса:
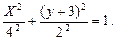
Центр эллипса находится в точке с координатами (0, -3), полуоси эллипса равны 4 и 2.
Определяем координаты точки М при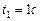 
:
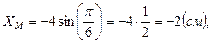
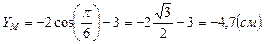
Точка М имеет координаты (-2, -4,7).
Определяем скорость точки:
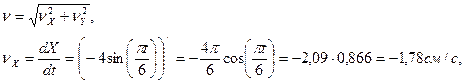
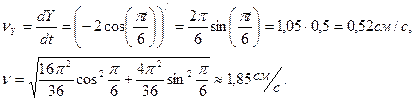
Определяем полное ускорение точки.
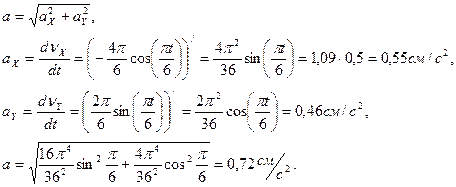
Определяем тангенциальное, нормальное ускорение точки, а также радиус кривизны окружности:
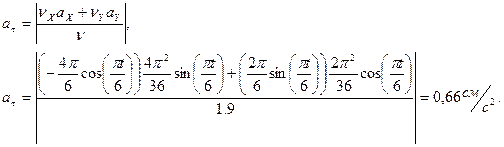
Нормальное ускорение:
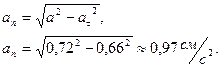
Радиус кривизны траектории:
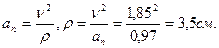
Строим траекторию движения точки, на которой указываем положение точки М по ее координатам, а также векторы скорости, нормального, тангенциального и полного ускорения (рис. 5.2).
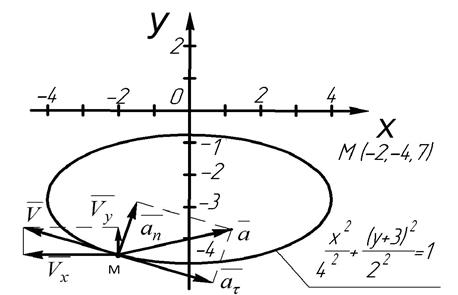
Рис.5.2
Пример 5.2
Определить вид траектории движения точки, найти ее положение при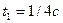 
, а также определить ее скорость, нормальное, тангенциальное, и полное ускорение точки, если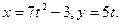 
Решение:
Определим вид траектории в координатной форме, исключив переменную из уравнений координат, найдем зависимость:
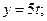
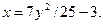
Траекторией движения точки является парабола, ветви которой вытянуты вдоль оси ОХ, вершина в О (-3,0) (рис.5.3).
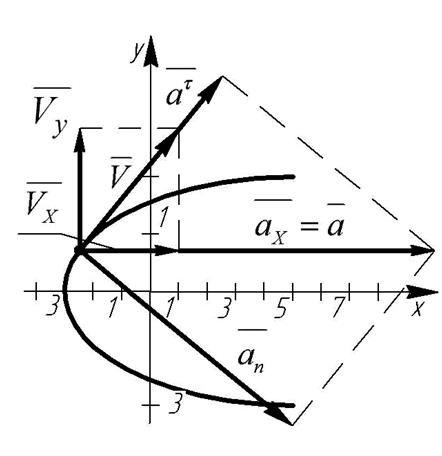
Рис.5.3
Определяем координаты точки М при 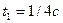, для этого в уравнение движения подставляем 
:
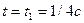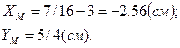
Покажем точку М на траектории
Определяем скорость точки:
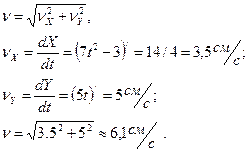
Определяем полное ускорение точки.
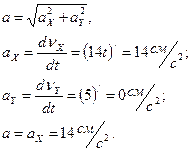
Определяем тангенциальное, нормальное ускорение точки, а также радиус кривизны окружности:
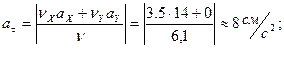
Нормальное ускорение:
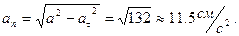
Радиус кривизны траектории:
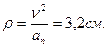
Покажем на рисунке 5.3 скорост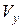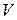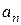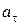и 
, 
, 
, 
, 
и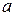 
точки М.