К-1. КИНЕМАТИКА ТОЧКИ. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ
По заданным в таблице 5.1 уравнениям движения точки М необходимо определить:
- вид её траектории;
- положение точки М на траектории для момента времени t=t1 cек;
- скорость точки М;
- полное, касательное, нормальное ускорение точки М;
- радиус кривизны траектории.
Таблица 5.1
Исходные данные для задачи К-1
| № п/п | Уравнения движения |  t1, с t1, с
| |
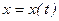 , см , см
| 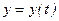 , см , см
| ||
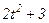
| 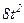
| 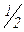
| |
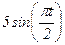
| 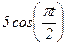 - 4 - 4
| ||
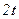
| 
| 
| |
| t–4 | 2–3t2 | ||
| 
| ||
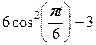
| 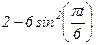
| ||
 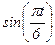 -5 -5
| 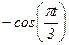 -2 -2
| ||
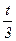
| t | ||
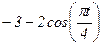
| 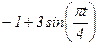
| ||
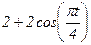
| 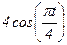
| ||
| 7t2–t+1 | 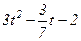
| ||
| 2t | 4t2–1 | 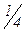
| |
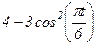
| 
| ||
| 
| ||
| 2t+4 | 
| 
| |
| 
| ||
| 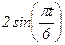
| ||
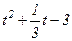
| 3t2+t+3 | ||
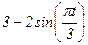
| 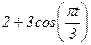
| ||
| –4t2+3 | 2t | 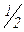
| |
| 4–2t | 2–4t2 | 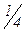
| |
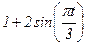
| 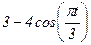
| ||
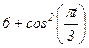
| 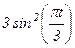
| ||
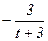
| 3t+9 | 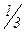
| |
| 4t2+3t+1 | 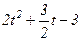
| ||
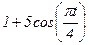
| 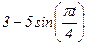
| ||
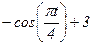
| 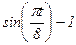
| ||
| 8t–3 | 2t–1 | 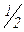
| |
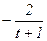
| 3t+3 | 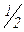
| |
| t3 | 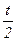
|
Практическое занятие 6
Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях
6.Указания к решению задач [1,4,5,6]
Расчет следует начинать с ведущего звена. При этом следует учесть, что когда два колеса находятся в зацеплении, то скорость точки зацепления каждого колеса одна и та же, а когда колеса связаны ременной передачей, то скорости всех точек ремня, а следовательно, точек, лежащих на ободе на каждого из этих колес, в данный момент времени числено одинаковы; при этом считается, что ремень по ободу колеса не проскальзывает. Колеса, находящиеся на одной оси вращения, а также стержень 6 с соответствующим колесом следует рассматривать как одно твердое тело с одинаковыми угловой скоростью и угловым ускорением.
Пример 6.1
Механизм состоит (рис.6.1) из ступенчатых колес 1-3, находящихся в зацеплении или связаны ременной передачей, груз 4 и 5 и стрелки 6, жестко связанной с колесом 3. радиусы колес равно соответственно: 1- r1=2 см, R1=4 см, у колеса 2- r2=6 см, R2=8 см, у колеса 3- r3=12 см, R3=16 см, длина стрелки l=24 см. Закон изменения скорости груза 5: υ5=2(t2-3) см/с2, положительное направление которой вниз.
Найти скорости точек А и С, угловое ускорение колеса 3 и ускорение точек B и D и груза 4 в момент t1 =2 с.
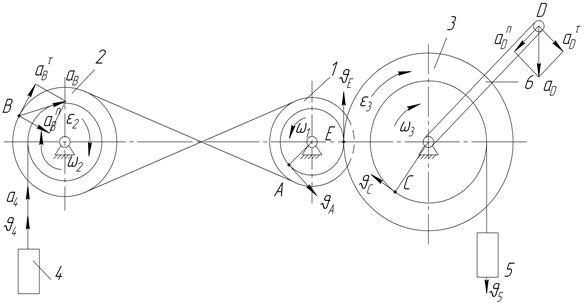
Рис. 6.1
Решение:
1. Определим сначала угловые скорости колес, как функции времени t. Зная υ5, находим угловую скорость 3-го колеса:
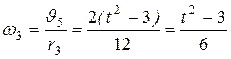 .
.
Так как колесо 3 и 1 находятся в зацеплении, то скорость точки Е зацепления этих колес одинакова, поэтому:
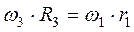 ,
,
Откуда:
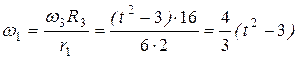 .
.
Колесо 1 находится в зацеплении с колесом 2, поэтому:
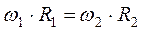 ,
,
откуда 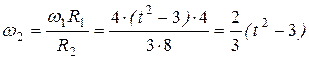 .
.
Направления угловых скоростей всех тел показаны на рис.6.1.
2.Определение углового ускорения 3-го тела ε3. По известной угловой скорости ω3:
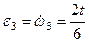 и при t1 =2 c. ε3 =0,67с-2.
и при t1 =2 c. ε3 =0,67с-2.
3.Определение скорости точки А. по известной угловой скорости 1-го колеса:
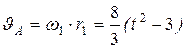 ,
,
при t1 =2 c. 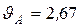 см/с.
см/с.
4.Определение скорости точки С. Так как точка С принадлежит колесу 3, то при t1 =2 c:
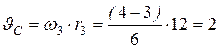 см/с.
см/с.
Направление скоростей точек А и С показаны на рисунке в соответствии с направлениями угловых скоростей.
5.Определение ускорения точки В. Предварительно находим угловое ускорение 2-го тела:
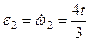 ,
,
при t1 =2 c. ε2 =2,67с-2.
Ускорение точки В:
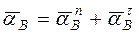 ,
,
причем 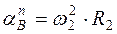 ,
,
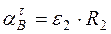 ,
,
при t1 =2 c.
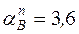 см/с2,
см/с2,
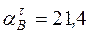 см/с2,
см/с2,
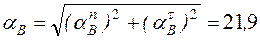 см/с2.
см/с2.
Направление 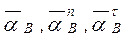 показаны на рисунке 6.1.
показаны на рисунке 6.1.
6.Определение ускорения точки D. При t1 =2 c:
ε3 =0,67с-2, ω3=0,17с-1.
Находим 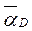 при t1 =2 c:
при t1 =2 c:
 ,
,
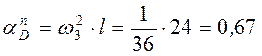 см/с2,
см/с2,
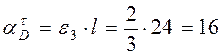 см/с2,
см/с2,
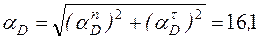 см/с2.
см/с2.
Направление 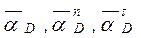 показаны на рисунке 6.1.
показаны на рисунке 6.1.
7.Определение ускорения тела 4. сначала находим скорость этого тела
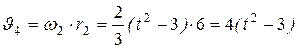 .
.
Так как груз 4 движется поступательно, то центр этого груза движется прямолинейно, а поэтому:
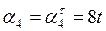 ,
,
при t1 =2 c, 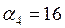 см/с2.
см/с2.
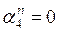 т.к.
т.к. 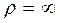 .
.
Замечание. Ускорение тела 4 можно найти как касательное ускорение точки обода колеса радиусом r2 т.е:
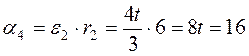 см/с2.
см/с2.
Задачи для выполнения расчетно-графической работы