ЗАДАЧА Д-2.1. Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней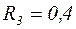 
м, 
м и радиусом инерции относительно оси вращения 
м, блока 4 радиуса 
м и катка (или подвижного блока) 5 (рис. 14.13, табл. 14.1); тело 5 считать сплошным однородным цилиндром, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость 
. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости 
.
Под действием силы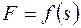 
, зависящей от перемещения 
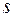точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент 
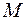сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение 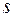станет равным 
м. Искомая величина указана в столбце «Найти» таблицы, где обозначено: 
, 
, 
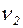- скорости грузов 1, 2 и центра масс тела 5 соответственно, 
и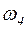 
- угловые скорости тел 3 и 4. Все катки, включая и катки, обмотанные нитями, катятся по плоскостям без скольжения.
Указания. Задача Д-2 - на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия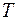 
системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении 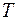для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей (кинематика). При вычислении работы надо все перемещения выразить через заданное перемещение 
, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
Таблица 14.1
Исходные данные для задачи Д-2.1
| вариант | I | II | III | ||||||
 ,
кг
|  ,
кг
|  ,
кг
|  ,
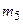кг
|  ,
кг
|  , Н/м
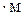
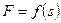|  , н 
|  , Н
| Найти | |
| 1,3 | 40(4+5 s) |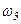 
| |||||||
| 0,9 | 50(8+3 s) |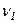 
| |||||||
| 1,2 | 60(6+5 s) |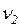 
| |||||||
| 1,5 | 70(5+6 s) |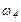 
| |||||||
| 1,3 | 80(9+4 s) |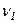
| |||||||
| 1,8 | 40(7+8 s) | 
| |||||||
| 0,6 | 50(8+9 s) |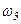
| |||||||
| 1,4 | 60(8+5 s) | 
| |||||||
| 1,2 | 70(9+2 s) |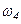 
| |||||||
| 1,8 | 80(6+7 s) |
| |||||||
| 1,3 | 30(4+3 s) |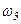
| |||||||
| 0,9 | 50(6+2 s) |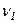
| |||||||
| 1,2 | 40(5+6 s) |
| |||||||
| 1,5 | 60(8+5 s) |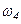
| |||||||
| 1,8 | 70(4+3 s) |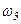
| |||||||
| 1,6 | 60(5+2 s) |
| |||||||
| 1,4 | 50(7+7 s) |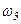
| |||||||
| 1,8 | 60(6+5 s) |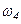
|
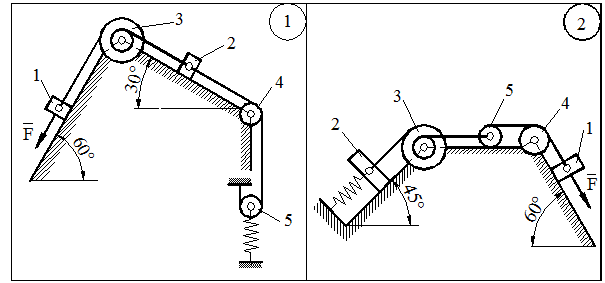
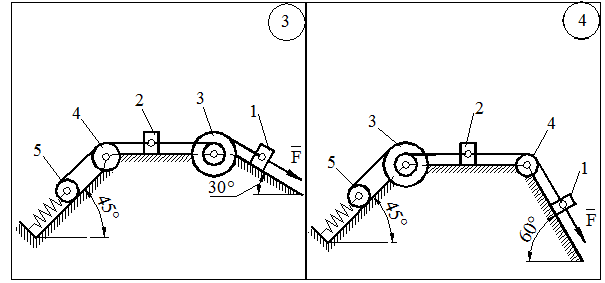
Рисунок 14.13
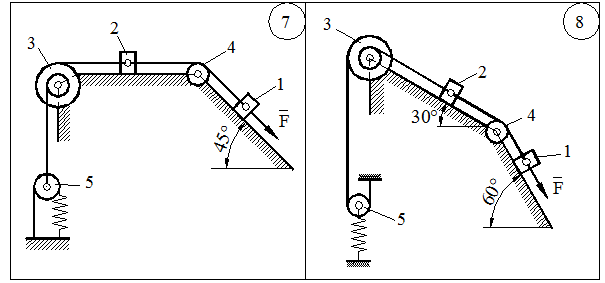
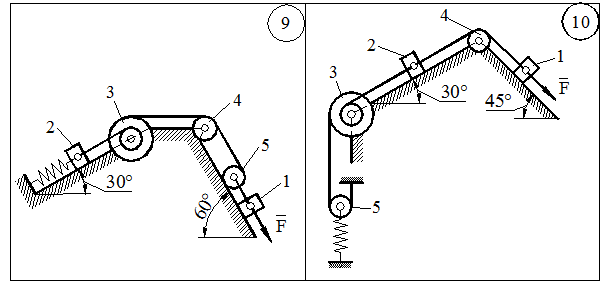
Рисунок 14.13 –окончание
ЗАДАЧА Д 2.2. Механическая система (рис. 14.14) приводится в движение из состояния покоя под действием пары с моментом или силы 
. Масса тележки с грузом или одного груза 1 
задана в таблице14.2; масса четырех колес тележки 2 
;масса барабана с колесом 3 
; масса колеса 4 
; массой подвижного блока 2 пренебречь. Наружный радиус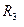 
задан в таблице 14.2; 
; 
; 
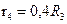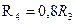; радиус инерции тела 3 
. Колеса тележки 2 и колесо 4 считать сплошными цилиндрами, трос – невесомой, нерастяжимой нитью. Колеса тележки катятся по наклонной плоскости 
без проскальзывания. При движении на барабан 3 действует момент сил сопротивления 
.
С помощью теоремы об изменении кинетической энергии определить величину М или Р из условия движения тележки с грузом или одного груза с заданным ускорением 
, а также их мощность через 
после начала движения.
Таблица 14.2
Исходные данные для задачи Д-2.2
| № условия | , кг
|  , м
| 
|
|
| 0,1 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,33 0,37 0,48 0,45 0,29 0,32 0,31 0,39 | 0,5 0,4 0,35 0,3 0,3 0,25 0,25 0,2 0,32 0,41 0,26 0,28 0,29 0,25 0,24 0,27 |
Рис.14.14
Рис.14.14 продолжение
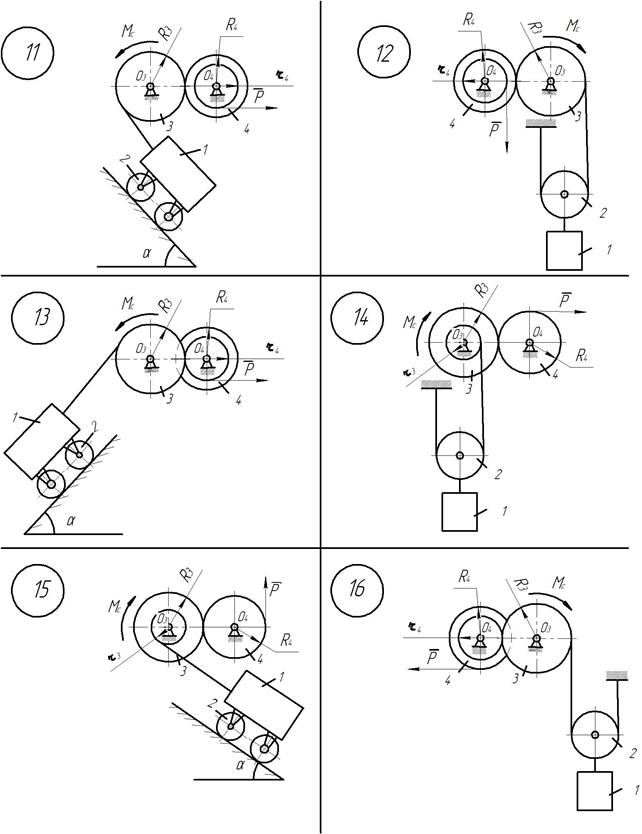
Рис.14.14-окончание
Практическое занятие 15