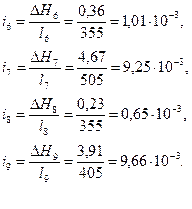Из формулы расхода выражаем диаметр трубы:

где Q – расход, 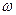 – площадь сечения, v – скорость.
– площадь сечения, v – скорость.
По ГОСТу при диаметре трубы меньшей или равной 250мм, скорость течения в ней воды варьируется от 0.6 до 1 м/с.
Принимаем диаметр трубопровода равный 100 мм, при заданном расходе вычислим скорость в трубопроводе:
При d = 100 мм
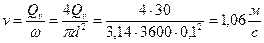 .
.
II.2. Геометрическая высота всасывания:
Для расчета предельной геометрической высоты установки (всасывания) центробежного насоса воспользуемся уравнением Бернулли для сечения 1-1 и 2-2

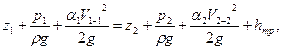
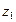 = 0 - геометрическая высота,
= 0 - геометрическая высота,
 =
=  давление в среде,
давление в среде,
 =1-коэффициент Кориолиса,
=1-коэффициент Кориолиса,
 =0 – скорость движения воды,
=0 – скорость движения воды,
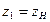 , т.к. высота
, т.к. высота 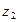 соответствует высоте располож. насоса,
соответствует высоте располож. насоса,
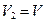 , т.к. скорость воды в трубопроводе постоянна,
, т.к. скорость воды в трубопроводе постоянна,
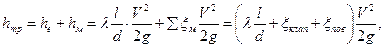

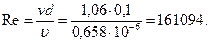
Определим области гидравлического сопротивления, для этого вычислим:
|



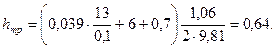
Вычислим предельную высоту установки насоса:
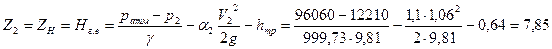 м.
м.
II.3. Вычислим кавитационный запас:
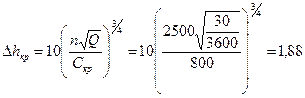 м,
м,
 м.
м.
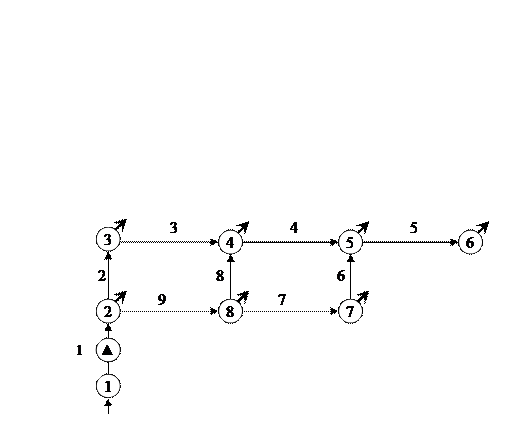
III. Задача №3: Потокараспределения в кольцевой трубопроводной сети
Схема системы подачи и распределения воды: в окружностях указаны номера узлов; над дугами – номера дуг; на дуге 1 – насосная станция; направление дуги указывает направление потока
Напорно-расходная характеристика насоса:
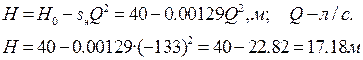
III.1. Получение напоров в узлах и расходов по участкам
1.1. Составим уравнение баланса расходов в каждом узле нашей сети
 1. х1 = -Q1
1. х1 = -Q1
2. x2 + x9 – x1 = -Q2
3. x3 – x2 = -Q3
(1) 4. x4 – x3 –x8 = -Q4
5. x5 – x4 – x6 = -Q5
6. –x5 = -Q6
7. x6 – x7 = - Q7
8. x7 + x8 – x9 = -Q8
Построение математической модели кольцевого трубопровода.
Составим матрицу полученной системы А (матрица инцинденций):
 участок узел участок узел
| |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | -1 | ||||||||
| -1 | -1 | ||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 |
Обозначим:
| Q1 | |
| -Q2 | |
| -Q3 | |
| b = | -Q4 |
| -Q5 | |
| -Q6 | |
| -Q7 | |
| -Q8 |
 x1 x1
| |
| x2 | |
| x3 | |
| x = | x4 |
| x5 | |
| x6 | |
| x7 | |
| x8 x9 |

Ах = b (1)
 Система линейно-зависима, т.к. ∑Qi=0 и при сложении всех уравнений системы (1) получили 0 = 0, поэтому одно уравнение можно вычеркнуть; получим усеченную матрицу A:
Система линейно-зависима, т.к. ∑Qi=0 и при сложении всех уравнений системы (1) получили 0 = 0, поэтому одно уравнение можно вычеркнуть; получим усеченную матрицу A:
 участок узел участок узел
| |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | -1 | ||||||||
| -1 | -1 | ||||||||
| -1 | |||||||||
| -1 |
и усеченный вектор:
 Q1 Q1
| |
| -Q2 | |

| -Q3 |
| b = | -Q4 |
| -Q5 | |
| -Q6 | |
| -Q7 |

 Тогда уравнение баланса расходов принимает вид:Ax = b (2)
Тогда уравнение баланса расходов принимает вид:Ax = b (2)
1.2. Составляем уравнение Бернулли для всех участков сети, например для первого участка оно имеет вид:
 Участок 1:
Участок 1: 
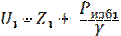
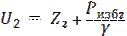
Аналогично составляя уравнения Бернулли для всех остальных участков, получим след. систему уравнений:
Аналогично составляя уравнения Бернулли для всех остальных участков, получим след. систему уравнений:
 1. U1- U2= (S1+Sн)|x1|·x1-H0
1. U1- U2= (S1+Sн)|x1|·x1-H0
2. U2 - U3 = S2·|x2|·x2
3. U3 - U4 = S3·|x3|·x3
4. U4 - U5 = S4·|x4|·x4
(3) 5. U5 - U6 = S5·|x5|·x5
6. U7 – U5 = S6·|x6|·x6
7. U8 – U7 = S7·|x7|·x7
8. U8- U4 = S8·|x8·|x8
9. U2 – U8 = S9·|x9|·x9
Выпишем матрицу системы (3) AT– транспонированную матрицу
 участок узел участок узел
| ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 | ||||||||
| -1 |
| (S1+Sн)|x1|·x1 | |
| S2·|x2|·x2 | |
| S3·|x3|·x3 | |

| S4·|x4|·x4 |
| f(x)x= | S5·|x5|·x5 |
| S6·|x6|·x6 | |
| S7·|x7|·x7 | |
| S8·|x8·|x8 | |
| S9·|x9|·x9 |

| -H0 |
| f(0)= | |



 f(x)=f(x)x+f(0)
f(x)=f(x)x+f(0)
 Тогда в матричном виде получили:
Тогда в матричном виде получили:
AT·U = f(x)x+f(0)
III.2. систему нелинейных уравнений
Таким образом, для нахождения неизвестных U и х имеем след.:



Ax = b (2)
AT·U = f(x)x+f(0) (3)
Из составленных уравнений мы получили 9 переменных Х, 8 переменных U, всего 9+8=17- переменных и 7+9=16 - уравнений. Чтобы решить систему уравнений (2) и (3) нужно задать значение одной из переменных, в нашем случае задан напор в первом узле Н1=15м.
Решая систему с помощью математической программой Maple,
> restart;with(linalg):with(LinearAlgebra):with(SumTools):Digits:=6:
check:=1;
x0:=vector([1,1,1,1,1,1,1,1,1]);
while check>0.001 do
A1:=matrix([
#[1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8],
[1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[-1,1,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0],
[0,-1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,-1,1,0,0,0,-1,0,0,0,0,0,0,0,0,0],
[0,0,0,-1,1,-1,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,-1,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,1,-1,0,0,0,0,0,0,0,0,0,0],
#[0,0,0,0,0,0,1,1,-1,0,0,0,0,0,0,0,0],
[-(88.6545*10^(-6)+0.00129)*x0[1],0,0,0,0,0,0,0,0,1,-1,0,0,0,0,0,0],
[0,-(336.7175*10^(-6))*x0[2],0,0,0,0,0,0,0,0,1,-1,0,0,0,0,0],
[0,0,-(1023.84*10^(-6))*x0[3],0,0,0,0,0,0,0,0,1,-1,0,0,0,0],
[0,0,0,-(4086.46*10^(-6))*x0[4],0,0,0,0,0,0,0,0,1,-1,0,0,0],
[0,0,0,0,-(22451.55*10^(-6))*x0[5],0,0,0,0,0,0,0,0,1,-1,0,0],
[0,0,0,0,0,-(13174.05*10^(-6))*x0[6],0,0,0,0,0,0,0,-1,0,1,0],
[0,0,0,0,0,0,-(4086.46*10^(-6))*x0[7],0,0,0,0,0,0,0,0,-1,1],
[0,0,0,0,0,0,0,-(2872.66*10^(-6))*x0[8],0,0,0,0,-1,0,0,0,1],
[0,0,0,0,0,0,0,0,-(1023.84*10^(-6))*x0[9],0,1,0,0,0,0,0,-1],
[0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0]]):
f0:=vector([133,0,-22,-24,-25,-15,-28,-40,0,0,0,0,0,0,0,0,15]):
y:=evalm(evalm(1/A1) &* f0):
check:=abs(y[1]-x0[1]);
For i from 1 to 9 do
x0[i]:=y[i];
end do;
end do;
>

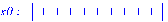
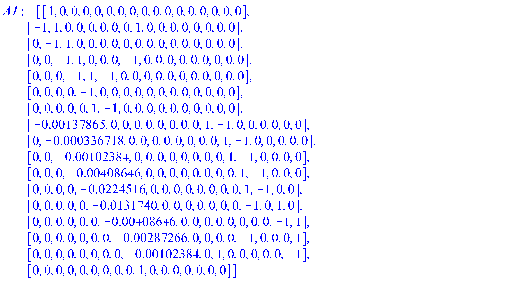
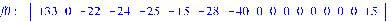



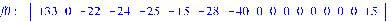

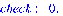

нашли следующие искомые значения расхода на участке х и напоры в узлах U:
| Номер участка | Расход на участке
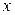 , л/c , л/c
|
| 133,00 | |
| 66,74 | |
| 44,74 | |
| 31,74 | |
| 8,26 | |
| 36,26 | |
| 11,00 | |
| 66,26 |
| Номер узла | Напор в узле U, м |
| 30,61 | |
| 28,92 | |
| 26,47 | |
| 21,71 | |
| 16,66 | |
| 22,07 | |
| 26,70 |
III.3. Рассчитаем потери напора ΔН, м на каждом участке :
1. ΔH1 =U1 - U2 +Нн = 15 – 30,61+17.18 = 1,57 м,
2. ΔH2=U2 – U3 = 30,61 – 28,92 = 1,69 м,
3. ΔH3=U3 – U4 = 28,92 – 26,47 = 2.45 м,
4. ΔH4=U4 - U5 = 26,47 – 21,71 = 4,76 м,
5. ΔH5=U5 – U6= 21,71 – 16,66 = 5,05 м,
6. ΔH6=U7 - U5 = 22,07– 21,71 = 0,36 м,
7. ΔH7=U8 - U7 = 26,70 – 22,07= 4,63 м,
8. ΔH8=U8 – U4 = 26,70 – 26,47 = 0,23 м,
9. ΔH9=U2 –U8 = 30,61 – 26,70 = 3,91 м.
III.4. Рассчитаем давление в узлах
Pизбi = (Ui – zi)·γ,
где z –высота узла (zi=1, i=1,…,8),
γ – удельный вес,
γ = ρ·g = 1000· 9.81 = 9810 H/м3.
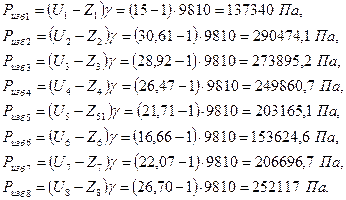
pабсi= Pизбi+pатмi
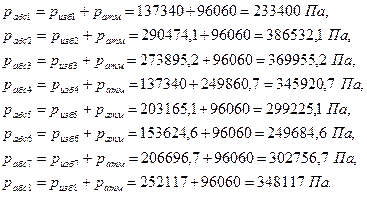
III.5. Пьезометрические уклоны участков
 .
.