Многочлены над полем. Теорема о делении с остатком.
НОД двух многочленов.
Пусть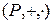 
поле. В кольце P[ x ] имеет место теорема, аналогичная теореме о делении с остатком в кольце 
.
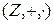Теорема1. Для любых многочленов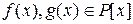 
, 
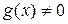существует и притом единственная пара многочленов 
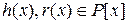, что
f (x) =g (x) ·h (x) +r (x), r (x) = 0 или ст. r (x) <ст. g (x). (5)
Доказательство. Покажем существование многочленов ,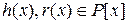
удовлетворяющих условию (1). Доказательство проведем методом
математической индукции по степени многочлена f (x).
Пусть ст. g (x) =m, g (x) =bmxm+bm- 1 xm- 1 +…+b 1 x+b 0.
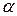) Если f (x) нулевой многочлен или ст. f (x) <m, то 
.
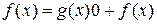В этом равенстве h (x) = 0, r (x) =f (x). Пусть теперь f (x) – многочлен степени n,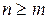 
. an – старший коэффициент многочлена f (x).
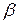) Предположим, что 
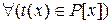ст. t(x)<n существуют такие многочлены 
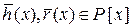, что имеет место равенство (5).
Рассмотрим многочлен
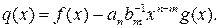(6)
Так как многочлены f (x),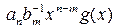 
имеют одну и ту же степень, то q (x) = 0, либо ст.q (x) <n. Если q (x) = 0, то из (6) следует 
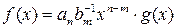. Здесь 
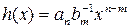, r (x) = 0. Рассмотрим случай, когда 
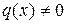. Так как ст.q (x) <n, то по индуктивному предположению 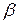) существуют многочлены 
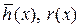, что
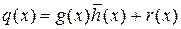, r (x) = 0 
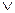ст. r (x) <ст. g (x). (7)
Из (6), (7) следует, что
f (x) =g (x) h (x) +r (x), r (x) = 0 или ст. r (x) <ст. g (x),
.
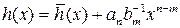Единственность. Предположим, что существуют многочлены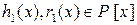 
, что f (x) можно представить в виде
f (x) =g (x) h 1(x) +r 1 (x), r 1(x) = 0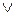 
ст. r 1(x) <ст. g (x). (8)
Из (5), (8) следует, что
(h (x) -h 1(x)) g (x) =r 1(x) -r (x), (9)
где r 1(x) -r (x) = 0или ст. (r 1(x) -r (x)) <ст.g (x)
Если предположить, что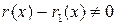 
, то из (9) получим: ст. (h (x) -
- h 1(x)) + ст.g (x) = ст. (r 1(x) - r (x)). Отсюда следует, что ст.g (x)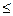 
ст. (r 1(x) - r (x)).
Пришли к противоречию. Значит, r 1(x) = r (x). Но тогда h (x) =h 1(x).
Наибольший общий делитель многочленов.
Пусть P [ x ] – кольцо многочленов над полем P.
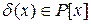называется общим делителем многочленов f 1(x), f 2(x), …, f n(x), если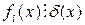 
.
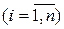Многочлен d (x) называется наибольшим общим делителем многочленов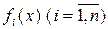 
, если
а) d (x) общий делитель многочленов ;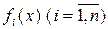
b) d (x) делится на любой общий делитель этих многочленов.
Из определения следует, что НОД многочленов определен с точностью до ненулевого множителя из поля P. Действительно, пусть d (x),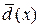 
наибольшие общие делители многочленов 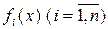. Тогда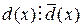 
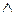
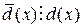. Существуют многочлены 
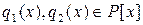, что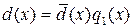 
, 
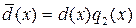. Из этих равенств получим d (x)(1 -q 1(x) q 2(x))=0. Так как P[ x ] не содержит делителей нуля, 
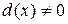, то из последнего равенства имеем: q 1(x) q 2(x)=1. Отсюда следует, что ст.q 1(x)+ст.q 2(x) = 0. Значит, q 1(x) =а, q 2(x) =с, 
, 
, 
.
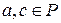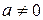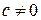Лемма. Пусть для многочленов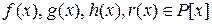 
имеет место равенство f(x)=g (x) h (x) +r (x). Тогда НОД(f (x), g (x)) = НОД(g(x), r (x)).
Нахождение НОД двух многочленов.
Пусть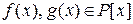 
, 
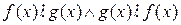. Разделим многочлен f (x) на g (x) с остатком: f (x) =g (x) h (x) +r 1(x), ст.r 1(x) <ст.g (x). Разделим теперь g (x) на r 1(x) с остатком: g (x) =r 1(x) h 1(x) +r 2(x), ст.r 2(x) <ст.r 1(x). И так далее. Этот процесс последовательного деления будем продолжать до тех пор пока не получим нулевой остаток. Так как ст.g (x), ст.r 1(x), ст.r2 (x), … - убывающая последовательность натуральных чисел, то она конечная. Поэтому на каком-то шаге последовательного деления получим остаток равный нулю.
Пусть r n+1(x)=0. В результате имеем:
f (x) = g (x) h (x)+ r 1(x), ст. r 1(x)<ст. g (x),
g (x) = r 1(x) h 1(x)+ r 2(x), ст. r 2(x)<ст. r 1(x),
r 1(x) = r 2(x) h 2(x) + r 3(x), ст. r 3(x)<ст. r 2(x), (10)
………………………………………………….
r n - 1 (x) =r n(x) h n(x) +r n + 1(x), r n + 1(x) = 0.
Из равенств (10) в силу леммы получим, что НОД(f (x), g (x)) = =НОД(g (x), r 1(x)) =НОД(r 1(x), r 2(x))= … = НОД(r n-1(x), r n(x))= НОД(r n(x), 0) = r n(x).
Таким образом, справедливо утверждение.
Теорема 2. Наибольший общий делитель многочленов ,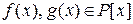 
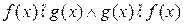равен с точностью до ненулевого множителя из поля P последнему ненулевому остатку в алгоритме Евклида для многочленов f (x), g (x).
Пример. Найти наибольший общий делитель многочленов f (x) =x 4 + 2 x 3 – x2 – 4 x- 2, g (x) = x 4 +x 3 - x 2 - 2 x -2.
Решение. К многочленам f (x) g (x) применим алгоритм Евклида: f (x) =
= g (x) + х 3-2 х, g (x) =(х 3-2 х)(х +1) + х 2-2 х, х 3 - 2 х = (х 2-2) х. Из этих равенств следует, что НОД(f (x), g (x)) = х 2 - 2.
Теорема 3. Пусть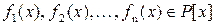 
. Если (f 1(x), f 2(x)) = d 1(x), (f 3(x), d 1(x)) = d 2(x), …, (fn (x), dn -2(x)) = dn -1(x), то (f 1(x), f 2(x), …, fn (x)) = dn -1(x).