Перестановки с повторениями.

Прочитать лекцию, выписать в тетрадь определения и формулы понятий: перестановки, размещения, сочетания. Переписать по одному примеру на каждое понятие.

Поочередный и одновременный выбор

Наука, изучающая способы составления и количество множеств и их подмножеств, называется комбинаторикой. Каждое конкретное подмножество, составленное из элементов данного конечного множества, называется соединением или выборкой. Если во множестве определено, какой элемент множества за каким следует или какому предшествует, то множество называется упорядоченным. Если в упорядоченном множестве изменить расположение элементов, то мы получим другое, отличное от первого множество. Выборка — результат отбора, извлечение предпочитаемого из наличного. Комбинаторная задача состоит в подсчете числа выборок из конечного основного множества элементов M = {a₁, а₂, а₃,..., а_n}. Выборки отличаются объемом (т.е. числом элементов, которые надо выбрать), порядком (т.е. упорядоченные или неупорядоченные выборки) и повторениями (есть или нет в выборке повторяющиеся элементы).Мы знаем три основных вида соединений: размещения, перестановки и сочетания.

Упорядоченные выборки (Поочередный выбор).

Размещения с повторениями.

Пример 1. Сколько трехзначных чисел можно составить из 4 цифр: 1, 2, 3, 4?

Решение: Перечислим с помощью схемы все возможные числа: Видим, что всего данных чисел 4³ = 64, где 4 — количество элементов исходного множества, а 3 — число выбранных элементов. Данный пример является иллюстрацией к следующему понятию: Размещениями из n элементов по k называются упорядоченные выборки, каждое из которых содержит k элементов из n данного множества. Размещения отличаются друг от друга либо порядком элементов, либо самими элементами. Если некоторые элементы данного множества могут повторяться в размещении, то такие размещения называются кортежами или размещениями с повторениями. Число элементов в размещении называют его длиной. Размещениями с повторениями называют упорядоченную выборку, состоящую из n не обязательно различных элементов.

Пусть дано множество M = {a₁, а₂, а₃,..., а_n}. Сколько кортежей длины k можно составить из n элементов этого множества?

Решение: Первый элемент каждого кортежа мы можем выбрать n способами, записав на первое место любой из n элементов. Второй элемент тоже можно выбрать n способами и т.д. Значит, общее число кортежей из множества n элементов, по k элементов в каждом, будет равно n^k. Число кортежей из n по k с учетом их порядка обозначается , и называют числом размещений с повторениями из n элементов по k: .

В примере 1: .

Перестановки с повторениями.

Пример 2. Сколько четырехзначных чисел можно составить из 4 цифр: 1, 2, 3, 4? Решение: Перечислим с помощью схемы все возможные числа: Видим, что всего данных чисел 4⁴ = 256. Данный пример является иллюстрацией к следующему понятию, которое является частным случаем, когда наше основное множество состоит из различных элементов: Размещения с повторениями из n не обязательно различных элементов основного множества по n принято называть перестановками с повторениями. Число перестановок с повторениями обозначают .Заметим, . Общее число перестановок с повторениями из n элементов равно .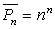

В примере 2: .

Пример 3. Сколько семизначных чисел можно составить из 7 цифр: 1; 1; 2; 2; 2; 3; 4?

Решение: Заметим, что «1» повторяется 2 раза, «3» — три раза, а «3» и «4» — по одному. На этот случай существует другая формула перестановок с повторениями. В общем случае, когда в нашем основном множестве какие-то элементы могут повторяться используют понятие:

Перестановкой с повторениями состава (k₁,k₂,…,k_n) из букв (a₁,a₂,…,a_n) называют любой кортеж длины k = k₁ + k₂ +…+ k_n, в который буква a₁ входит k₁ раз, буква a₂ входит k₂ раз,…, буква a_n входит k_n раз. Число таких перестановок обозначают P(k₁,k₂,…,k_n) и вычисляют по формуле: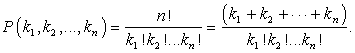

В примере 3:

Размещения без повторений (Размещения).

Пример 4. Сколько трехзначных чисел, в которых цифры не повторяются, можно составить из 4 цифр: 1, 2, 3, 4?

Решение: Перечислим с помощью схемы все возможные числа:

Видим, что всего данных чисел 4·3·2 = 24. Данный пример является иллюстрацией к следующему понятию: Пусть множество M = {a₁, а₂, а₃,..., а_n}. Сколько размещений без повторения элементов, по k элементов в каждом, можно составить из элементов этого множества?

Решение: На первое место можно записать любой элемент из М. Значит, имеем n возможностей. На второе место — любой элемент, кроме выбранного на первое место. Итак, при каждом выборе первого элемента для выбора второго имеем n-1 возможностей, т.е. для выбора двух элементов имеем n (n— 1) возможностей. При каждом выборе первых двух элементов для выбора третьего элемента имеем n— 2 возможностей и т.д. На последнее k -е место можно записать любой элемент, кроме выбранных k—1 элементов на предыдущие места, т.е. для его выбора имеем n — (k — 1) = n — k + 1 возможностей. Следовательно, всего размещений из n по k элементов будет . Полученное выражение состоит из k последовательных натуральных множителей, наибольший из которых равен n. Умножив и разделив полученное выражение на (n - k)! получим: 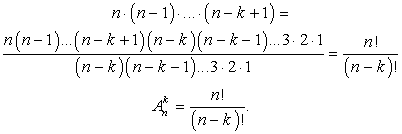Размещениями называют упорядоченную выборку k элементов из n различных элементов основного множества. Число всех выборов k элементов из n различных элементов данного множества с учетом их порядка обозначают А_n^k и называют числом размещений из n элементов по k.

В примере 4: .

Перестановки без повторений (Перестановки).

Пример 5. Сколько четырехзначных чисел, в которых цифры не повторяются, можно составить из 4 цифр: 1, 2, 3, 4? Решение:Перечислим с помощью схемы все возможные числа: Видим, что всего данных чисел 4·3·2·1 = 24. Данный пример является иллюстрацией к следующему понятию: Размещения из n элементов по n принято называть перестановками. Иначе, перестановки — это упорядоченные множества из n различных элементов основного множества по n. Перестановки отличаются друг от друга только порядком элементов. Число перестановок принято обозначать Р_n. Общее число перестановок из n элементов равно P_n = n!

В примере 5: P₄ = 4! = 4·2·3·1 = 24.