Сочетания без повторений (Сочетания).
Пример 6. Сколько трехэлементных подмножеств, различающихся хотя бы одним элементом друг от друга и без учета порядка в подмножестве, можно составить из 4 цифр: 1, 2, 3, 4?
Решение: 
Перечислим все полученные подмножества: (1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4). Видим, что всего получилось 4 подмножества. Данный пример является иллюстрацией к следующему понятию: Сочетания. Сочетаниями из n элементов по k называются соединения, каждое из которых содержит k элементов из данного множества n элементов и отличается от других хотя бы одним элементом. В сочетаниях нас интересуют только сами элементы множества и не интересует их порядок. Важно, какие конкретно элементы множества входят в каждое соединение. Число сочетаний, т.е. число всех различных подмножеств длины k из данного множества, содержащего n элементов, обозначается Сnk. Легко видеть, что если мы возьмем все сочетания из n по k и в каждом из них упорядочим элементы всеми возможными способами, т.е. из каждого сочетания получим все возможные перестановки, то получим все размещения из n элементов по k. Значит, Ank = Сnk·Pk. Отсюда 
или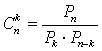 
. Иначе 
В примере 6: 
.
Пример 7. Сколькими способами можно выбрать k предметов из n? Например:
а) одновременно вынимают две карты из колоды: 
б) наугад зачеркивают 6 чисел из 49: 
в) случайно отбирают трех человек из 25: 
Сочетания с повторениями.
Сочетания с повторениями — неупорядоченная выборка, состоящая из n необязательно различных элементов. Обозначается 
. 
где n – количество необязательно различных элементов основного множества, k – количество выбираемых.
Пример 8. Сколько будет костей в игре домино, если использовать, только четыре цифры 1, 2, 3, 4?
Решение: Используем формулу сочетаний с повторениями: 
Ответ: 10.
Задачи для тренировки
Пример 9. Сколько четырехзначных чисел можно составить из 9 цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9?
Решение: Цифры в числах могут повторяться, и число зависит от порядка цифр в его записи. Значит, это размещения с повторениями, т.е. кортежи. Их число
Ответ: 6561.
Пример 10. В чемпионате участвует 12 команд. Сколькими различными способами могут быть распределены три различные медали?
Решение:
Это размещения без повторения, т.к. одна команда не может занять два или три места сразу. А123 = 12·11·10 = 1320.
Ответ: 1320.
Пример 11. В семье 6 человек. За столом 6 стульев. В семье решили каждый вечер рассаживаться на эти 6 стульев по-новому. Сколько дней члены семьи смогут делать это без повторений?
Решение: Одного человека мы можем посадить только один раз. Значит, имеем перестановки без повторений. Одно размещение от другого может отличаться только порядком размещения людей, т.е. имеем перестановки 6 элементов: P6= 6! = 720.
Ответ: 720.
Пример 12. Сколько «слов» можно получить, переставляя буквы в слове «математика»?
Решение: Слово «математика» является кортежем длины 10, имеющим состав (2,3,2,1,1,1) (буква «м» входит два раза, буква «а» — 3 раза, буква «т» — два раза, буквы «е», «и», «к» по одному разу). Значит, при перестановках букв получится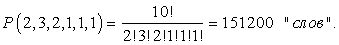 
Ответ: 151 200.
Пример 13. У мамы было 2 яблока, 3 груши, и 4 апельсина. Каждый день она давала ребенку по одному фрукту. Сколькими способами она может это сделать?
Решение: 
Ответ: 1260.
Пример 14. Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать капитана команды для математических соревнований и его заместителя?
Решение:
1-й способ: На роль капитана может быть выбран любой из 30 учащихся, а его заместитель – любой из 29 оставшихся учеников. Таким образом, получаем 30·29 = 870 способов. 2-й способ: Порядок важен, тогда по формуле числа размещений имеем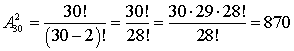 
способов.
Ответ: 870.
Пример 15. Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать двоих для участия в математической олимпиаде?
Решение:
1-й способ: Нам не важно, кто капитан, а кто заместитель, нам нужны всего лишь два участника, поэтому получаем, что у нас каждая пара учащихся в произведении повторяется два раза. Поэтому ответом для второй задачи будет (30·29):2 =435. 2-й способ: Без учета порядка применим формулу числа сочетаний 
.
Ответ: 435.
Пример 16. Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр?
Решение: Так как кнопки нажимаются одновременно, то выбор этих кнопок — сочетание. Отсюда возможно 
вариантов.
Пример 17. Три собаки выбегают из дома, догоняя кошку. Сколькими способами они смогут это сделать?
Решение: Порядок выбегания из дома задает нумерацию трех собак числами 1 2 3. Таких нумераций 3! = 6.
Ответ: 6.
Пример 18. Сколькими способами можно построить пятерых человек в шеренгу?
Решение: По формуле числа перестановок имеем Р5 = 5·4·3·2·1 = 120.
Ответ: 120.
Пример 19. Сколькими способами 4 человека могут по одному разбежаться на все 4 стороны?
Решение: Стороны фиксированы, например юг, север, запад, восток или для простоты 1 2 3 4. Порядок разбегания по ним задает нумерацию 4 воров числами 1 2 3 4. Таких нумераций имеется 4! =24.
Ответ: 24.
Пример 20. 11 футболистов строятся перед началом матча. 1-м — обязательно капитан, 2-м — обязательно вратарь, а остальные — случайным образом. Сколько существует способов построения?
Решение: Капитана и вратаря строить не надо, т.к. их места фиксированы. 9 футболистов (все, кроме капитана и вратаря) надо расставить на 9 мест — с 3-го по 11-е. Всего имеется 9! = 362 880 таких перестановок.
Ответ: 362 880.
Пример 21. В классе 27 учеников, из которых нужно выбрать троих. Сколькими способами это можно сделать, если: а) 1-й ученик должен решить задачу, 2-й — сходить за мелом, 3-й — пойти дежурить в столовую; б) им следует спеть хором?
Решение:
а) Порядок важен: А273 = 27·26·25 = 17 550
б) Порядок неважен: 
.
Ответ: а) 17 550, б) 2 925.
Пример 22. В коридоре 3 лампочки. Сколько существует различных способов освещения коридора? (включая случай, когда все три не горят)
Решение: 1-й способ: Пронумеруем лампочки. 1-я: горит или не горит (2 исхода), 2-я: горит или не горит (2 исхода), 3-я: горит или не горит (2 исхода). Лампочки горят или нет независимо друг от друга. По правилу умножения: 2 · 2 · 2 = 8.
2-й способ: Приведем дерево вариантов данной задачи: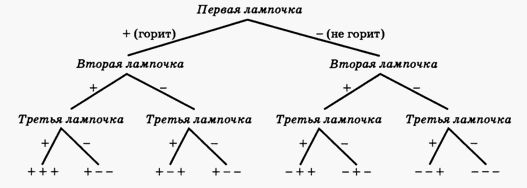 
Например, (+ - +) означает, что горят 1-я и 3-я, (---) — не горит ни одна и т.д. в нашем случае у трехэлементного множества 23 =8 подмножеств.
Пример 23. У бармена есть 6 сортов зеленого чая. Для проведения чайной церемонии требуется подать зеленый чай ровно 3 различных сортов. Сколькими способами бармен может выполнить заказ?
Решение: Тут все просто: есть n = 6 сортов, из которых надо выбрать k = 3 сорта. Число сочетаний можно найти по формуле: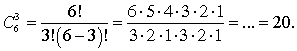 
Ответ: 20.
Пример 24. В чемпионате по футболу 7 команд. Каждая команда играла с каждой один раз. Сколько всего было игр?
Решение: Порядок выбора не имеет значения, т.е. если выбраны две команды, то неважно, какая из них первая, а какая — вторая: 
Ответ: 21.
Пример 25. Сколько всего исходов, если друг за другом из колоды вынимают две карты, не возвращая карту обратно (выбор без возвращения)?
Решение: 
Ответ: 1260.
Пример 26. Сколько существует всего исходов, если из колоды вынимают две карты одновременно?
Решение:
Порядок не важен, значит: 
Ответ: 630.
Пример 27. Сколько будет костей в игре домино, если использовать 8 цифр?
Решение:
Используем формулу сочетаний с повторениями: 
Ответ: 36.