ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПЕРИОДА И ЧАСТОТЫ СВОБОДНЫХ КОЛЕБАНИЙ НИТЯНОГО МАЯТНИКА ОТ ЕГО ДЛИНЫ

Федеральное государственное образовательное учреждение высшего образования «Балтийский федеральный университет имени Иммануила Канта» Институт природопользования, территориального развития и градостроительства

 

 

ПРОЕКТНАЯ РАБОТА

«Исследование математических колебаний»

 

Специальность: 07.02.01 Архитектура

 

 

Разработала студентка

Группы А-11

___________А.А. Егорова

Руководитель

___________Е.Х. Тавгер

Консультант

___________И.О. Сидоренко

 

 

Калининград

2020 г.

СОДЕРЖАНИЕ

 

ВВЕДЕНИЕ. 3

1 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ.. 5

1.1 Гармонические колебания. 7

1.2 Негармонические колебания. 11

1.3 Свободные колебания. 12

1.4 Вынужденные колебания. 13

2 ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПЕРИОДА И ЧАСТОТЫСВОБОДНЫХ КОЛЕБАНИЙ НИТЯНОГО МАЯТНИКА ОТ ЕГО ДЛИНЫ.. 20

2.1 Проведение серии экспериментов. 21

2.2 Вывод. 22

2.3 Математическая зависимость между длиной маятника и периодом колебаний

ЗАКЛЮЧЕНИЕ. 25

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ.. 26

 

ВВЕДЕНИЕ

Работа посвящена изучению различных колебаний. Колебательные процессы в природе чрезвычайно разнообразны, реализуясь практически в любых материальных объектах (как органических, так и неорганических). Кроме того, колебательные процессы порождают целый мир волновых явлений, связанных с распространением колебательного процесса в любых материальных средах за счёт взаимодействия структурных элементов среды (атомов и молекул) между собой. Колебания относятся к классу периодических процессов, в которых характер движения повторяется с изменением интервала времени T, называемого периодом колебания. В общем случае характер колебания может быть очень сложным. Однако, надёжную методическую основу для исследования и, соответственно, понимания периодических процессов создаёт изучение простейшего варианта колебаний, малых колебаний механических систем вблизи положений равновесия. Принципиально важно, что малые колебания любых конструкций математически описываются гармоническими функциями (синусами и косинусами). Поэтому гармонический анализ является рабочим инструментом любого конструктора. Знание спектра собственных частот колебаний любых механизмов, машин, сооружений исключительно важно для того, чтобы избежать катастрофических последствий резонансного разрушения в условиях эксплуатации изделий. Таким образом, изучая колебания, мы будем обращать внимание не только на то, что «волнуется» и что «колеблется», а главным образом на то, как и почему происходят колебания.

Цель работы: исследовать математические колебания и их зависимость от периода и частоты свободных.

 

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Исходя из заявленной темы исследовательской работы «Исследование математических колебаний», считаем необходимым остановиться вначале на устройстве, которое непосредственно является так называемым математическим маятником.

Математическим маятником называют материальную точку с массой m, подвешенную на тонкой нерастяжимой невесомой нити (или невесомом стержне), колеблющуюся в поле тяготения Земли. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен и не зависит от амплитуды колебаний и массы маятника.

Заметим, что в положении равновесия (нить расположена вертикально) сила тяжести уравновешивается силой натяжения нити.

При отклонении маятника из положения равновесия на некоторый угол появляется сила, направленная в сторону, противоположную отклонению маятника. Формула периода колебания этого маятника была выведена голландским ученым Гюйгенсом (1629-1695 гг.). Этот современник И. Ньютона очень увлекался данной механической системой. В 1656 г. он создал первые часы с маятниковым механизмом. Они измеряли время с исключительной для тех времен точностью. Это изобретение стало важнейшим этапом в развитии физических экспериментов и практической деятельности.

Если маятник находится в положении равновесия (висит отвесно), то сила тяжести будет уравновешиваться силой натяжения нити. Плоский маятник на нерастяжимой нити является системой с двумя степенями свободы со связью. При смене всего одного компонента меняются характеристики всех ее частей. Так, если нитку заменить на стержень, то у данной механической системы будет всего одна степень свободы.

Математический маятник имеет очень интересные свойства. Все они подтверждаются известными физическими законами. Период колебаний любого другого маятника зависит от разных обстоятельств, таких как размер и форма тела, расстояние между точкой подвеса и центром тяжести, распределение массы относительно данной точки. Именно поэтому определение периода висящего тела является довольно сложной задачей. Намного легче вычисляется период математического маятника, формула которого будет приведена ниже. В результате наблюдений над подобными механическими системами можно установить такие закономерности:

- Если, сохраняя одинаковую длину маятника, подвешивать различные грузы, то период их колебаний получится одинаковым, хотя их массы будут сильно различаться. Следовательно, период такого маятника не зависит от массы груза.

- Если при запуске системы отклонять маятник на не слишком большие, но разные углы, то он станет колебаться с одинаковым периодом, но по разным амплитудам.

Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными, гармоническими и негармоническими.

 

 

Гармонические колебания

Простейшим видом колебательного процесса являются колебания, происходящие по закону синуса или косинуса, называемые гармоническими колебаниями. Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω ₀ задаётся следующим образом:

Решение предыдущего уравнения является уравнением движения для гармонических колебаний, которое имеет вид:

где: x – смещение тела от положение равновесия, A – амплитуда колебаний, то есть максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний (ω = 2 Π / T), t – время. Величина, стоящая под знаком косинуса: φ = ωt + φ ₀, называется фазой гармонического процесса. Смысл фазы колебаний: стадия, в которой колебание находится в данный момент времени. При t =0 получаем, что φ = φ ₀, поэтому φ ₀ называют начальной фазой (то есть той стадией, из которой начиналось колебание).

Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Если же количество колебаний N, а их время t, то период находится как:

Физическая величина, обратная периоду колебаний, называется частотой колебаний:

 

Частота колебаний ν показывает, сколько колебаний совершается за 1 с. Единица частоты – Герц (Гц). Частота колебаний связана с циклической частотой ω и периодом колебаний T соотношениями:

Рисунок 1 показывает гармонические колебания тел с разными положениями тел. Данный эксперимент наблюдается в специальных условиях при наличии периодических вспышек освещения, называемого стробоскопическим. Для изображения векторов скорости тела в разные моменты времени используют стрелки.

Рисунок 1 - Стробоскопическое изображение гармонических колебаний. Начальная фаза φ0=0φ0=0. Интервал времени между последовательными положениями тела τ = T12τ = T12.

На графике 2.1.3.2.1.3. показаны изменения, происходящие во время гармонического процесса, при изменении амплитуды колебаний xmxm, или периода Т Т (частоты ff), или начальной фазы φ0φ0.

 

Рисунок 2 - Во всех трех случаях для синих кривых φ0=0φ0=0: aa – красная кривая отличается от синей только большей амплитудой (x'm>xm)(x'm>xm); bb – красная кривая отличается от синей только значением периода (T'=T2)(T'=T2); сс – красная кривая отличается от синей только значением начальной фазы (φ′0=−π2 рад) φ0'=-π2 рад.

 

Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:

Максимальное значение скорости при гармонических механических колебаниях:

Максимальные по модулю значения скорости υ _m = ωA достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a = ax тела при гармонических колебаниях. Зависимость ускорения от времени при гармонических механических колебаниях:

Максимальное значение ускорения при механических гармонических колебаниях:

Знак минус в предыдущем выражении означает, что ускорение a (t) всегда имеет знак, противоположный знаку смещения x (t), и, следовательно, возвращает тело в начальное положение (x = 0), т.е. заставляет тело совершать гармонические колебания.

Следует обратить внимание на то, что:

физические свойства колебательной системы определяют только собственную частоту колебаний ω ₀ или период T.

Такие параметры процесса колебаний, как амплитуда A = x _m и начальная фаза φ ₀, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени, т.е. начальными условиями.

При колебательном движении тело за время, равное периоду, проходит путь, равный 4 амплитудам. При этом тело возвращается в исходную точку, то есть перемещение тела будет равно нулю. Следовательно, путь равный амплитуде тело пройдет за время равное четверти периода.

Чтобы определить, когда в уравнение колебаний подставлять синус, а когда косинус, нужно обратить внимание на следующие факторы:

- Проще всего, если в условии задачи колебания названы синусоидальными или косинусоидальными.

- Если сказано, что тело толкнули из положения равновесия – берем синус с начальной фазой, равной нулю.

- Если сказано, что тело отклонили и отпустили – косинус с начальной фазой, равной нулю.

- Если тело толкнули из отклоненного от положения равновесия состояния, то начальная фаза не равна нолю, а брать можно и синус и косинус.

 

1.2 Негармонические колебания

Негармоничесие колебания – это колебания которые не происходят по закону синуса и косинуса.

Реальные колебания не происходят в точности по гармоническому закону. Ни один колебательный процесс в природе и технике не продолжается бесконечно долго, а имеет начало и конец во времени. А колебательный процесс, ограниченный во времени, не является гармоническим. Шарик, подвешенный на нити, и груз, подвешенный на пружине, совершают колебания, которые лишь близки к гармоническим. Сопротивление воздуха, необратимые потери энергии на нагревание нити и пружины при их деформации приводят к тому, что амплитуда колебаний уменьшается, и колебания становятся негармоническими.

 

1.3 Свободные колебания

Колебания считают свободными (собственными) в том случае, если они выполняются только за счет энергии, которая была сообщена колебательной системе в начальный момент времени и далее внешние воздействия на эту систему отсутствуют.

Все такие тела или совокупности тел, которые сами по себе могут совершать периодические движения, или колебания, называют колебательными системами.

Всем колебательным системам присущ ряд общих свойств. Рассмотрим главные из них:

- У каждой колебательной системы есть состояние устойчивого равновесия. У физического маятника - это положение, в котором центр масс подвешенного шарика находится на одной вертикали с точкой подвеса; у вертикального пружинного маятника - положение, в котором сила тяжести уравновешивается силой упругости пружины; у горизонтального пружинного маятника - положение, при котором обе пружины деформированы одинаково.

- После того как колебательная система выведена из положения устойчивого равновесия, появляется сила, возвращающая систему в устойчивое положение. Происхождение этой силы может быть различным. Например, у физического маятника - это равнодействующая силы тяжести и силы реакции нити, а у пружинных маятников - сила упругости пружин.

- Возвратившись в устойчивое состояние, колеблющееся тело не может сразу остановится. Этому мешает его инертность.

Перечисленные свойства приводят к тому, что если колебательную систему тем или иным способом вывести из состояния устойчивого равновесия,

то в ней в отсутствие внешних сил возникнут и некоторое время будут сохраняться колебания.

 

1.4 Вынужденные колебания

Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.

В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.

Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω₀.

Если свободные колебания происходят на частоте ω₀, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы.

После начала воздействия внешней силы на колебательную систему необходимо некоторое время Δ t для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания τ свободных колебаний в колебательной системе.

В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω₀. Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы.

Рассмотрим в качестве примера вынужденные колебания тела на пружине (рис. 3). Внешняя сила приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 2.5.1) конец пружины перемещаться по закону:

y = y _m cos ω t.

где y _m – амплитуда колебаний, ω – круговая частота.

Такой закон перемещения можно обеспечить с помощью шатунного механизма, преобразующего движение по окружности в поступательно-возвратное движение (рис. 2.5.1).

Рисунок 3 - Вынужденные колебания груза на пружине. Свободный конец пружины перемещается по закону y = ym cos ωt. l – длина недеформированной пружины, k – жесткость пружины

Если левый конец пружины смещен на расстояние y, а правый – на расстояние x от их первоначального положения, когда пружина была недеформирована, то удлинение пружины Δ l равно:

Δ l = x – y = x – y _m cos ω t.

Второй закон Ньютона для тела массой m принимает вид:

ma = – k (x – y) = – kx + ky _m cos ω t.

В этом уравнении сила, действующая на тело, представлена в виде двух слагаемых. Первое слагаемое в правой части – это упругая сила, стремящаяся возвратить тело в положение равновесия (x = 0). Второе слагаемое – внешнее периодическое воздействие на тело. Это слагаемое и называют вынуждающей силой.

Уравнению, выражающему второй закон Ньютона для тела на пружине при наличии внешнего периодического воздействия, можно придать строгую математическую форму, если учесть связь между ускорением тела и его координатой: Тогда уравнение вынужденных колебаний запишется в виде

 

 

где 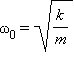– собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 4) величина A определяется выражением:

Уравнение не учитывает действия сил трения. В отличие от уравнения свободных колебаний уравнение вынужденных колебаний это уравнение содержит две частоты – частоту ω₀ свободных колебаний и частоту ω вынуждающей силы.

Установившиеся вынужденные колебания груза на пружине происходят на частоте внешнего воздействия по закону:

x (t) = x_mcos (ωt + θ).

Амплитуда вынужденных колебаний x _m и начальная фаза θ зависят от соотношения частот ω₀ и ω и от амплитуды < m >m>y_m внешней силы.

На очень низких частотах, когда ω << ω₀, движение тела массой m, прикрепленного к правому концу пружины, повторяет движение левого конца пружины. При этом x (t) = y (t), и пружина остается практически недеформированной. Внешняя сила приложенная к левому концу пружины, работы не совершает, т. к. модуль этой силы при ω << ω₀ стремится к нулю.

Если частота ω внешней силы приближается к собственной частоте ω₀, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. Зависимость амплитуды x _m вынужденных колебаний от частоты ω вынуждающей силы называется резонансной характеристикой или резонансной кривой (рис. 5).

При резонансе амплитуда x _m колебания груза может во много раз превосходить амплитуду y _m колебаний свободного (левого) конца пружины, вызванного внешним воздействием. В отсутствие трения амплитуда вынужденных колебаний при резонансе должна неограниченно возрастать. В реальных условиях амплитуда установившихся вынужденных колебаний определяется условием: работа внешней силы в течение периода колебаний должна равняться потерям механической энергии за то же время из-за трения. Чем меньше трение (т. е. чем выше добротность Q колебательной системы), тем больше амплитуда вынужденных колебаний при резонансе.

Рисунок 4 - Модель. Вынужденные колебания

 

У колебательных систем с не очень высокой добротностью (< 10) резонансная частота несколько смещается в сторону низких частот. Это хорошо заметно на рис. 2.5.2.

Явление резонанса может явиться причиной разрушения мостов, зданий и других сооружений, если собственные частоты их колебаний совпадут с частотой периодически действующей силы, возникшей, например, из-за вращения несбалансированного мотора.

 

Рисунок 5 - Резонансные кривые при различных уровнях затухания:

1 – колебательная система без трения; при резонансе амплитуда xm вынужденных колебаний неограниченно возрастает; 2, 3, 4 – реальные резонансные кривые для колебательных систем с различной добротностью: Q2 > Q3 > Q4. На низких частотах (ω << ω0) xm ≈ ym. На высоких частотах (ω >> ω0) xm → 0

Вынужденные колебания – это незатухающие колебания. Неизбежные потери энергии на трение компенсируются подводом энергии от внешнего источника периодически действующей силы. Существуют системы, в которых незатухающие колебания возникают не за счет периодического внешнего воздействия, а в результате имеющейся у таких систем способности самой регулировать поступление энергии от постоянного источника. Такие системы называются автоколебательными, а процесс незатухающих колебаний в таких системах – автоколебаниями. В автоколебательной системе можно выделить три характерных элемента – колебательная система, источник энергии и устройство обратной связи между колебательной системой и источником. В качестве колебательной системы может быть использована любая механическая система, способная совершать собственные затухающие колебания (например, маятник настенных часов).

Источником энергии может служить энергия деформация пружины или потенциальная энергия груза в поле тяжести. Устройство обратной связи представляет собой некоторый механизм, с помощью которого автоколебательная система регулирует поступление энергии от источника. На рис. 6 изображена схема взаимодействия различных элементов автоколебательной системы.

 

Рисунок 6 - Функциональная схема автоколебательной системы

 

Примером механической автоколебательной системы может служить часовой механизм с анкерным ходом (рис. 2.5.4). Ходовое колесо с косыми зубьями жестко скреплено с зубчатым барабаном, через который перекинута цепочка с гирей. На верхнем конце маятника закреплен анкер (якорек) с двумя пластинками из твердого материала, изогнутыми по дуге окружности с центром на оси маятника. В ручных часах гиря заменена пружиной, а маятник – балансиром – маховичком, скрепленным со спиральной пружиной. Балансир совершает крутильные колебания вокруг своей оси. Колебательной системой в часах является маятник или балансир. Источником энергии – поднятая вверх гиря или заведенная пружина. Устройством, с помощью которого осуществляется обратная связь, является анкер, позволяющий ходовому колесу повернуться на один зубец за один полупериод. Обратная связь осуществляется взаимодействием анкера с ходовым колесом. При каждом колебании маятника зубец ходового колеса толкает анкерную вилку в направлении движения маятника, передавая ему некоторую порцию энергии, которая компенсирует потери энергии на трение. Таким образом, потенциальная энергия гири (или закрученной пружины) постепенно, отдельными порциями передается маятнику.

Механические автоколебательные системы широко распространены в окружающей нас жизни и в технике. Автоколебания совершают паровые машины, двигатели внутреннего сгорания, электрические звонки, струны смычковых музыкальных инструментов, воздушные столбы в трубах духовых инструментов, голосовые связки при разговоре или пении и т. д.

 

Рисунок 7 - Часовой механизм с маятником

 

 

ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПЕРИОДА И ЧАСТОТЫСВОБОДНЫХ КОЛЕБАНИЙ НИТЯНОГО МАЯТНИКА ОТ ЕГО ДЛИНЫ

Цель: выяснить, как зависит период и частота свободных колебаний математического маятника от его длины.

Оборудование: штатив с муфтой и лапкой, шарик с нитью, секундомер (рис. 1).

Рисунок 8 - Оборудование

 

Для выполнения работы нам потребуется таблица:

 

Величина/№
Длина (см)
Число колебаний
Время (с)
Период (с)
Частота (Гц)

 

Во-первых, нужно определить количество экспериментов. В данном случае их 5. По вертикали записаны те величины, которые мы будем измерять. В первую очередь, длина самого маятника в сантиметрах. Следующая величина – количество колебаний. Далее – полное время колебаний. Следующие две графы – это период колебаний, который измеряется в секундах, и частота в Гц. Следует обратить внимание на то, что я заранее записала те величины, которые буду использовать. В первую очередь, это длина нитяного маятника. Начальная длина: 5 см – это очень короткий маятник. Дальше 20, 45, 80 и 125. Число колебаний я буду использовать постоянное. Это 30 колебаний. В каждом эксперименте я буду использовать по 30 колебаний.

2.1 Проведение серии экспериментов

Соберем экспериментальную установку. Установка состоит из шарика на нити. Нить продернута через ластик. Это сделано для того, чтобы можно было регулировать его длину. Обратите внимание, что сам ластик укреплен в лапке штатива.

Рисунок 9 - Грузик на нити, закрепленный в штативе

Для измерения длины будем использовать линейку и секундомер. Итак, мы отсчитали 30 колебаний, и время, которое мы зарегистрировали, оказалось равным 13,2 с (рис. 3).

Рисунок 10 - Первый эксперимент с длиной нити 5 см

Заносим эти данные в таблицу и можем приступать к расчетам периода и частоты колебаний. Следующий шаг: увеличиваем длину маятника до 20 см. И весь эксперимент повторяем сначала. Вновь результаты заносим в таблицу. Итак, проведя эти эксперименты, я получила конечные результаты и занесла их в таблицу.

Период колебаний: (с). Частота колебаний: (Гц), где – это время, а – количество колебаний, совершенных за время .

Обратите внимание: когда длина маятника составляла 5 см, 30 колебаний прошли за время 13,2 с. Период колебаний составил , а частота .

Следующий результат: те же 30 колебаний, но длина маятника была уже 20 см. В этом случае увеличилось время колебаний – 26,59 с, а период колебаний составил . Частота уменьшилась почти в 2 раза, обратите внимание: .

Если мы посмотрим на третий результат, то увидим, что длина маятника еще больше, период стал больше, а частота уменьшилась еще на некоторое значение. Обратите внимание на то, как при 4 и 5 опытах будет меняться период и частота колебаний нашего нитяного маятника.

Величина/№
Длина (см)
Число колебаний
Время (с)	13,2	26,59	40,32	52,81	66,21
Период (с)	0,44	0,886	1,344	1,76	2,207
Частота (Гц)	2,27	1,128	0,744

 

 

2.2 Вывод

Можно сделать вывод: с увеличением длины маятника увеличивается период колебаний и уменьшается частота (рис. 4). Хотелось бы, чтобы четвертый и пятый опыты вы проделали сами и убедились, что все действительно так, как мы получили в наших опытах.

Формула для вычисления периода колебания математического маятника: , где – длина маятника, а – ускорение свободного падения.

Формула для вычисления частоты колебаний: .

Рисунок 11 - Зависимость частоты и периода маятника от его длины

2.3 Математическая зависимость между длиной маятника и периодом колебаний

Эта часть работы заключается в том, чтобы лучше определить взаимосвязь периода колебаний и длины нитяного маятника. Эта зависимость должна определяться математически. Цель дополнительного задания в том, чтобы выявить математическую зависимость между периодом и длиной маятника. Как это можно сделать? Нужно рассмотреть отношение периодов колебаний маятника и отношение длин маятника. Посмотрим на таблицу, которую используем, и обсудим те величины, которые будем туда заносить.

 

 

В первой части я рассмотрю отношение периода из второго опыта, когда длина маятника составляла 20 см. Отношение я буду искать к периоду, который получила, когда длина маятника составляла 5 см. Отношение самих длин я рассмотрю в нижней строке. Итак, в верхней строке отношение периодов , в нижней строке отношение длин маятника . Все необходимые данные я возьму из предыдущей таблицы. Обратим внимание, что эти вычисления в некоторых случаях получатся приближенными, но это зависит уже от чистоты эксперимента. Если мы обратимся к первой строке, то увидим, что во всех экспериментах отношение периодов будет составлять:

 

Далее рассмотрим отношение длин маятников. Обратите внимание: в первом случае это отношение равно 4, т. е. . Во втором случае – 9. В третьем случае – 16. Видно сразу, как будут связаны эти величины. Посмотрите: в первом случае у нас 2 и 4. В другом случае – 3 и 9 и т. д.

 

 

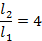
Делаем вывод о том, что период будет пропорционален корню квадратному из длины маятника. Эту зависимость мы можем использовать в дальнейшем для анализа подобных колебаний:

Из этого следует, что период мы можем записать как .

Другими словами, если мы увеличиваем длину маятника в 4 раза, то период увеличится в 2 раза. Если увеличим длину маятника в 3 раза, то увеличится период в раз. И т. д. В этом и заключается результат этой работы.

 

 

ЗАКЛЮЧЕНИЕ

Нужно признать, что:

- период колебаний Т не зависит от массы m маятника;

- при небольших отклонениях от положения равновесия период не зависит от амплитуды колебаний маятника (в пределах точности измерения времени ∆t = ± 0,1 секунды);

- период колебаний Т зависит от длины нити l подвеса маятника, причем квадрат периода Т² пропорционален длине нити подвеса l. Это означает, что выполняется равенство:

Т² = С l,

- где С- постоянная, имеющая физическую размерность [ С ] = c² /м. Из наших измерений следует, что С= Т² / l ≈ 4,84 /1,2 ≈ 4 c² /м.

- Постоянная С обратно пропорциональна важной физической величине- ускорению свободного падения тел вблизи поверхности Земли.

Благодаря вышеперечисленным работам было проведено практическое подтверждение ранее заявленной цели.

Эта тема актуальна, так как может пригодиться мне для дальнейшего изучения физических процессов и их применения на практике и создания новых научно-исследовательских проектах.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. Крылов А. Н. «Очерк истории установления основных начал механики» УФН 2 143–161(1921).

2. Лабораторный практикум по общей физике (колебания и волны) [Электронный ресурс]: – Режим доступа: https://lycu1580.mskobr.ru/ – (Дата обращения – 07.02.2020)

3. Механические колебания и волны [Электронный ресурс]: – Режим доступа: https://physics.ru/ – (Дата обращения – 07.02.2020)

4. Негармоническое колебание [Электронный ресурс]: – Режим доступа: https://www.ngpedia.ru/ – (Дата обращения – 07.02.2020)

5. Колебания [Электронный ресурс]: – Режим доступа: https://educon.by/ – (Дата обращения – 07.02.2020)

6. Аксенович Л.А. Физика в средней школе: Теория. Задания. Тесты: учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования/Л.А. Аксенович, Н.Н. Ракина, К.С. Фарино. Под ред. К.С. Фарино. – Минск.: Адукацыя i выхаванне, 2004.

7. Физика: механика. 10 кл.: учеб. для углубленного изучения физики/М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др. Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – 496 с.

8. Элементарный учебник физики. Под ред. Г.С. Ландсберга. Т. 3. – М., 1974.