истема m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У или СЛУ в разных источниках) в линейной алгебре — это система уравнение вида

| (1) |
Система линейных уравнений от трёх переменных определяет наборплоскостей. Точка пересечения является решением.
Здесь  — количество уравнений, а
— количество уравнений, а 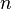 — количество неизвестных. x 1, x 2, …, xn — неизвестные, которые надо определить. Коэффициенты системы a 11, a 12, …, amn и свободные члены b 1, b 2, … bm предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].
— количество неизвестных. x 1, x 2, …, xn — неизвестные, которые надо определить. Коэффициенты системы a 11, a 12, …, amn и свободные члены b 1, b 2, … bm предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].
Система (1) называется однородной, если все её свободные члены равны нулю (b 1 = b 2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c 1, c 2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c 1(1), c 2(1), …, cn (1) и c 1(2), c 2(2), …, cn (2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
| c 1(1) = c 1(2), c 2(1) = c 2(2), …, cn (1) = cn (2). |
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется недоопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой
Прямые методы дают алгоритм, по которому можно найти точное решение СЛАУ. И если бы точность была абсолютной, они бы нашли его. Реальная ЭВМ, естественно, работает с погрешностью, поэтому решение будет приближённым.
Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.
Прямые методы [править | править вики-текст]
· Метод Гаусса
· Метод Гаусса — Жордана
· Метод Крамера
· Матричный метод
· Метод прогонки (для трёхдиагональных матриц)
· Разложение Холецкого или метод квадратных корней (для положительно-определённых симметричных и эрмитовых матриц)
· Метод вращений[3]
Итерационные методы [править | править вики-текст]
Итерационные методы устанавливают процедуру уточнения определённого начального приближения к решению. При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций. Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений. Суть этих методов состоит в том, чтобы найти неподвижную точку матричного уравнения
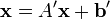 ,
,
эквивалентного начальной системе линейных алгебраических уравнений. При итерации  в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:
в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:
 .
.
Итерационные методы делятся на несколько типов, в зависимости от применяемого подхода:
· Основанные на расщеплении: 
· Вариационного типа: 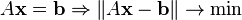
· Проекционного типа: 
Среди итерационных методов можно отметить самые популярные:
· Метод Якоби (метод простой итерации)[ источник не указан 1377 дней ]
· Метод Гаусса — Зейделя
· Метод релаксации
· Многосеточный метод
· Метод Монтанте
· Метод Абрамова (пригоден для решения небольших СЛАУ)
· Метод обобщённых минимальных невязок (англ.)
· Метод бисопряженных градиентов
· Стабилизированный метод бисопряжённых градиентов
· Квадратичный метод бисопряжённых градиентов (англ.)
· Метод квази-минимальных невязок (QMR)
·