Введение.
В настоящее время сложно представить школьный курс математики без понятия уравнение. Большинство задач сводятся к решению и применению различных видов уравнений. При этом уравнения, являются одним из средств моделирования явлений из окружающего нас мира и знакомство с ними, а также они являются существенной частью математического образования.
На практике и в научных задачах, где какую-то величину нельзя непосредственно измерить или вычислить по готовой формуле, удается составить соотношения, которым оно удовлетворяет. Из этого следует, что уравнение служит для определения неизвестной величины. Уравнения, являются важнейшей неотъемлемой частью науки и учебного предмета математики. В начальном курсе математики учитель старается знакомить младших школьников с данным понятием наглядно, путём созерцания конкретных примеров или практического оперирования ими, опираясь при этом на жизненный опыт учащихся.
В ходе рассмотрения понятия уравнения необходимо использовать следующие термины «уравнение», «корень уравнения», «что значит решить уравнение». При этом наряду с компонентами понятия уравнения, входящими в текст определения, надо включать и все другие его компоненты по мере развертывания материала данной линии. Таким образом, раскрыв сущность понятия «уравнение» в школьном курсе математики можно сказать о том, что под уравнением в математике понимается, вид равенства с неизвестной величиной, которая чаще всего обозначается латинской буквой. При этом числовое значение данной буквы, позволяющее получить верное равенство, называется корнем уравнения. В начальном курсе математики учитель старается знакомить младших школьников с данным понятием наглядно, путём созерцания конкретных примеров или практического оперирования ими, опираясь при этом на жизненный опыт учащихся.
Понятие «уравнение». Виды уравнений.
С начала 1 класса учащихся знакомят с понятиями: числовое выражение, равенство и неравенство.
Числовым выражением называют запись, состоящую из чисел, знаков действий и скобок. Например, 2+(6+4).
Числовым равенством называют запись, состоящую из чисел, знаков действий и знака равно (или: два выражения, соединенные знаком равно называют равенством). Например, 2+5=3+4.
Два выражения, соединенные знаками «больше» или «меньше» называют числовым неравенством. Например, 7+5<15.
Число, получаемое в результате выполнения всех действий в числовом выражении, называют значением числового выражения.
Если числовое значение найти нельзя, то говорят, что числовое выражение не имеет смысла. Например, 18: (12-12).
Формирование у учащихся понятия «уравнение» и «решение уравнения».
Подготовительный этап.
Начинается в первом классе. Учащиеся переходят к действиям над числами и выполняют задания, связанные с нахождением неизвестного числа в «окошке», например:
1) Среди чисел, записанных справа, подчеркните то число, при подстановке которого в окошко, получится верное равенство.
3+ □ =9 4, 5, 6, 7
□ - 2 = 4 1, 2, 3, 4, 5, 6

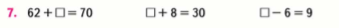
М.И. Моро, 2 класс, 1 часть.
2) Какие записи верны?
3 + 5 = 8 7 + 2 = 10 10 – 4 = 5
Как изменить результат, чтобы записи стали верными?
Дети находят число либо подбором, либо на основе знаний состава числа, либо на основе зависимости между компонентами и результатом действия.
2. Второй этап: знакомство учащихся с понятиями «уравнение» и «корень уравнения».
Учащимся сообщается, что в математике вместо □ используется латинские буквы (х, у, а, в, с) и такие записи называются уравнением: 3+х=6, 10: х = 5 и т.п.



И.И. Аргинская, 2к. 1ч. М.И. Моро, 2к. 1 ч.


Н.Б. Истомина, 4к. 1ч.
Важно на этом этапе закрепить у учащихся умение узнавать уравнение среди математических выражений:


И.И. Аргинская, 2к. 1ч.

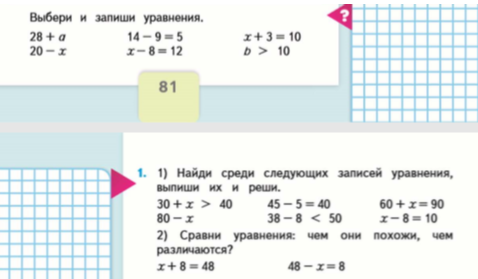
Н.Б. Истомина, 4 к.1ч. М.И. Моро 2 к. 1ч.
Уравнение– это равенство, содержащее неизвестное число, которое надо найти. Решить уравнение – значит найти все такие значения х (если они есть), при которых равенство будет верным.