Работа и мощность при поступательном движении
Работа постоянной силы P на прямолинейном участке пути s, пройденном точкой приложения силы, определяется по формуле
(1) A = Ps cos α,
где α – угол между направлением действия силы и направлением перемещения.
При α = 90°
cos α = cos 90° = 0 и A = 0,
т. е. работа силы, действующей перпендикулярно к направлению перемещения, равна нулю.
Если направление действия силы совпадает с направлением перемещения, то α = 0, поэтому cos α = cos 0 = 1 и формула (1) упрощается:
(1') A = Ps.
На точку или на тело обычно действует не одна сила, а несколько, поэтому при решении задач целесообразно использовать теорему о работе равнодействующей системы сил
(2) AR = ∑ Ai,
т. е. работа равнодействующей какой-либо системы сил на некотором пути равна алгебраической сумме работ всех сил этой системы на том же пути.
В частном случае, когда система сил уравновешена (тело движется равномерно и прямолинейно), равнодействующая системы сил равна нулю и, следовательно, AR=0. Поэтому при равномерном и прямолинейном движении точки или тела уравнение (2) принимает вид
(2') ∑ Ai = 0,
т. е. алгебраическая сумма работ уравновешенной системы сил на некотором пути равна нулю.
При этом силы, работа которых положительна, называются движущими, а силы, работа которых отрицательна, называются силами сопротивления. Например, при движении тела вниз – сила тяжести – движущая сила и ее работа положительна, а при движении тела вверх его сила тяжести является силой сопротивления и работа силы тяжести при этом отрицательна.
При решении задач в случаях, когда неизвестна сила Р, работу которой нужно определить, можно рекомендовать два приема (метода).
1. При помощи сил, заданных в условии задачи, определить силу P, а затем по формуле (1) или (1') вычислить ее работу.
2. Не определяя непосредственно силы P, определить Ap – работу требуемой силы при помощи формул (2) и (2'), выражающих теорему о работе равнодействующей.
Мощность, развиваемая при работе постоянной силы, определяется по формуле
(3) N = A/t или N = (Ps cos α)/t.
Если при определении работы силы Р скорость движения точки v=s/t остается постоянной, то
(3') N = Pv cos α.
Если же скорость движения точки изменяется, то s/t = vср – средняя скорость и тогда формула (2') выпажает среднюю мощность
Nср = Pvср cos α.
Коэффициент полезного действия (к. п. д.) при совершении работы можно определить как отношение работ
(4) η = Aпол/A,
где Aпол – полезная работа; A – вся произведенная работа, или как отношение соответствующих мощностей:
(4') η = Nпол/N.
Единицей работы в СИ служит 1 джоуль (Дж) = 1 Н * 1 м.
Единицей мощности в СИ служит 1 ватт (Вт) = 1 Дж / 1 сек.
Популярной внесистемной единицей мощности является лошадиная сила (л. с.):
1000 Вт = 1,36 л. с. или 1 л. с. = 736 Вт.
Для перехода между ваттами и лошадиными силами следует пользоваться формулами
N (кВт) = 1,36 N (л. с.)
N (л. с.) = 0,736 N (кВт).
Работа и мощность при вращательном движении
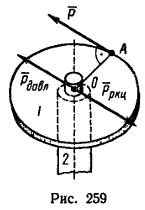
При вращательном движении тела движущим фактором является пара сил. Рассмотрим диск 1, могущий свободно вращаться вокруг оси 2 (рис. 259). Если к точке A на ободе диска приложить силу P (направим ее вдоль касательной к боковой поверхности диска; направленная таким образом сила называется окружным усилием), то диск станет вращаться. Вращение диска обусловлено появлением пары сил. Сила P, действуя на диск, прижимает его в точке O к оси (сила Pдавл на рис. 259, приложенная к оси 2) и возникает реакция оси (сила Pркц на рис. 259), приложенная так же, как и сила P, к диску. Так как все эти силы численно равны между собой и линии их действия параллельны, то силы P и Pркц образуют пару сил, которая и приводит диск во вращение.
Как известно, вращающее действие пары сил измеряется ее моментом, но момент пары сил равен произведению модуля любой из сил на плечо пары, поэтому вращающий момент
Mвр = Mпары = MOP = P*OA.
Единицей момента пары сил, а также момента силы относительно точки или относительно оси является 1 Н*м (ньютон-метр) в СИ и 1 кГ*м (килограмм-сила-метр) в системе МКГСС. Но при этом не следует смешивать эти единицы с единицами работы (1 Н*м=1 Дж или 1 кГ*м), имеющими ту же размерность.
Работу при вращательном движении производят пары сил.
Величина работы пары сил измеряется произведением момента пары (вращающего момента) на угол поворота, выраженный в радианах:
(1) A = Mврφ.
Таким образом, чтобы получить единицу работы, например, 1 Дж=1 Н*м, необходимо единицу момента 1 Н*м умножить на 1 рад. Но так как радиан – безразмерная величина
[радиан] = [длина дуги/радиус] = [м/м] = [1],
то
[Дж] = [Н*м] * [1] = [Н*м].
Мощность при вращательном движении
(2) N = A/t = Mврφ/t.
Если тело вращается с постоянной угловой скоростью, то, заменив в формуле (2) φ/t = ω, получим
(2') N = Mврω.
Если мощность того или иного двигателя – величина постоянная, то
(3) Mвр = N/ω,
т. е. вращающий момент двигателя обратно пропорционален угловой скорости его вала.
Это означает, что использование мощности двигателя при различных угловых скоростях позволяет изменять создаваемый им вращающий момент. Используя мощность двигателя при малой угловой скорости, можно получить большой вращающий момент.
Так как угловая скорость вращающейся части двигателя (ротора электродвигателя, коленчатого вала двигателя внутреннего сгорания и т. п.) при его работе практически не изменяется, то между двигателем и рабочей машиной устанавливается какой-либо механизм (редуктор, коробка скоростей и т. п.), могущий передавать мощность двигателя при различных угловых скоростях.
Поэтому формула (3), выражающая зависимость вращающего момента от передаваемой мощности и угловой скорости, имеет очень важное значение.
Используя при решении задач эту зависимость, необходимо иметь в виду следующее. Формула (3) применяется для решения задач, если мощность N задана в ваттах, а угловая скорость ω – в рад/сек (размерность [1/сек]), тогда вращающий момент Mвр получится в Н*м.