Сборник лабораторных работ
Методические указания
для студентов ФЭН всех форм обучения
и всех направлений
НОВОСИБИРСК
Составили: канд. техн. наук, доц. Ю.И. Шаров,
докт. техн. наук, проф. П.А. Щинников
Рецензент канд. техн. наук, доц. О.К. Григорьева
Работа подготовлена на кафедре Тепловых
электрических станций
Ó Новосибирский государственный
технический университет, 2011 г.
ОГЛАВЛЕНИЕ
Лабораторная работа № 1
Определение показателя адиабаты воздуха ……………………………………...4
Лабораторная работа № 2
Определение массовой изобарной теплоемкости воздуха ………………………7
Литература ………………………………………………………………………...14
Лабораторная работа № 1
Определение показателя адиабаты воздуха
Клеман и Дезорм в 1819 году предложили определять показатель адиабаты газов через отношение их изобарных и изохорных теплоемкостей:
. (2.1)
Воздух при повышенном давлении p 1 и температуре окружающей среды Т 1, находящийся в ресивере 4 объемом V 1 (рис.2.1), быстро выпускается в окружающую среду (адиабатное истечение 1-2). При истечении температура его понизится до 
. Затем быстро перекрывается трехходовой кран 2 и воздух через стенку ресивера изохорно подогревается до температуры окружающей среды Т * (процесс 2-3). Давление воздуха в ресивере при этом становится равным р 2. Уравнение адиабатного процесса
, (2.2)
или в дифференциальной форме:
,
откуда:
. (2.3)
Точки 1 и 3 лежат на изотерме 
. Уравнение изотермы:
, (2.4)
или в дифференциальной форме:
,
откуда:
. (2.5)
Левые части уравнений (2.3) и (2.5) равны. Приравниваем их правые части, разрешаем равенство относительно показателя адиабаты и заменяем бесконечно малые изменения давлений на конечные в процессах 1-2 и 1-3:
|
|
. (2.6)
В формулу (2.6) надо подставлять абсолютные давления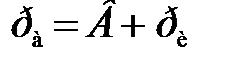 
, где В – атмосферное (барометрическое) давление. При подстановке абсолютных давлений в формулу (2.6) барометрические давления В в числителе и знаменателе сокращаются, то есть вместо абсолютных можно подставлять избыточные давления р 1 и р 2 в мм. вод. ст. Поскольку абсолютное давление в конце адиабатного истечения равно давлению окружающей среды 
, то избыточное 
. Тогда окончательная формула для определения показателя адиабаты:
. (2.7)
Методика выполнения работы
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Экспериментальная установка в опыте Клемана и Дезорма представлена на рис. 2.1. Установка состоит из ресивера 4, трехходового крана 2, дифференциального манометра 5, ручного насоса 1 и выхлопного клапана 3. Все основные элементы установки соединены между собой шлангами.
Трехходовой кран имеет три рабочих положения: в первом положении воздух из атмосферы нагнетается насосом в ресивер; во втором положении все рабочие каналы перекрыты, в третьем положении воздух из ресивера выпускается в атмосферу через выхлопной клапан.
2.2. Проведение эксперимента
1. Выравнивается давление в ресивере с атмосферным давлением (третье положение крана). При этом оба столба воды на дифференциальном манометре 5 должны показывать нулевой уровень.
2. Ручным насосом в ресивер нагнетается воздух (первое положение крана) до давления около 600…660 мм. вод. ст. Кран перекрывается (второе положение), тем самым ресивер изолируется от окружающей среды. При нагнетании воздуха возрастают его давление и температура. Затем воздух охлаждается через стенку ресивера до температуры окружающей среды Т * (изохорный процесс 5-1). Пропорционально абсолютной температуре воздуха снижается его давление до величины р 1.
|
|
3. Открывая на короткое время кран 2, соединяем ресивер 4 с выхлопным клапаном 3. Воздух с характерным шумом выходит в атмосферу (адиабатное истечение 1-2), при этом столбик воды на манометре быстро падает до атмосферного давления 
, а температура становится ниже атмосферной. Как только шум истечения прекратится и падение столба воды замедлится, кран необходимо закрыть. После изохорного нагрева воздуха 2-3 через стенку ресивера температура его станет равной атмосферной Т * и установится давление р 2.
Результаты наблюдений заносят в табл. 2.1.
Таблица 2.1
Таблица измерений
| Состояние | Единица измерения | Эксперимент | ||
| Точка 1 | мм. вод. ст. | р 1 = | р 1 = | р 1 = |
| Точка 3 | мм. вод. ст. | р 2 = | р 2 = | р 2 = |
2.3. Обработка результатов эксперимента
Расчеты выполняются в табл. 2.2.
Таблица 2.2
Таблица расчетов для воздуха
| № | Величина | Формула | Эксперимент | ||
Показатель адиабаты 
| 
| ||||
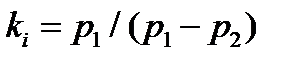
Среднее значение 
| 
| ||||
Изохорная теплоемкость  , Дж/(кг·К)
|  ,
 1005 Дж/(кг·К)
| ||||
| Газовая постоянная R, Дж/(кг·К) | 
| ||||
Молекулярная масса 
|  ,
 =8314 Дж/(кмоль·К)
| ||||
Погрешность  , %
| 
| ||||
Погрешность  , %
| 
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
|
|
1. Каким образом можно объяснить несовпадение экспериментальных результатов со справочными?
2. Чем будет отличаться pV -диаграмма эксперимента от теоретической, показанной на рис. 2.1?
3. Почему в эксперименте можно не учитывать атмосферное давление p *?
4. Каков физический смысл показателя адиабаты?
5. В чем заключается отличие показателя адиабаты от показателя политропы?
Лабораторная работа № 2
Определение массовой изобарной
теплоемкости воздуха
Теплоемкость – это теплота, которую необходимо подвести к единичному количеству вещества, чтобы нагреть его на 1 К. Единичное количество вещества можно измерить в килограммах, кубометрах при нормальных физических условиях и кило молях. Киломоль газа – это масса газа в килограммах, численно равная его молекулярной массе. Таким образом, существует три вида теплоемкостей: массовая c, Дж/(кг×К); объемная с¢, Дж/(м3×К) и мольная 
, Дж/(кмоль×К). Поскольку киломоль газа имеет массу в m раз больше одного килограмма, отдельного обозначения для мольной теплоемкости не вводят. Соотношения между теплоемкостями:
; 
; 
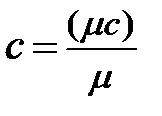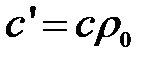, (1.1)
где 
= 22,4 м3/кмоль – объем киломоля идеального газа при нормальных физических условиях; 
– плотность газа при нормальных физических условиях, кг/м3.
Истинная теплоемкость газа – это производная от теплоты по температуре:
, (1.2)
Подведенная к газу теплота зависит от термодинамического процесса. Она может быть определена по первому закону термодинамики для изохорного и изобарного процессов:
, (1.3)
. (1.4)
Здесь 
– теплота, подведенная к 1 кг газа в изобарном процессе; 
– изменение внутренней энергии газа; 
– работа газов против внешних сил.
По существу формула (4) формулирует 1-е начало термодинамики, откуда следует уравнение Майера:
. (1.5)
Если положить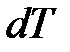 
= 1 К, то 
, то есть физический смысл газовой постоянной – это работа 1 кг газа в изобарном процессе при изменении его температуры на 1 К.
Уравнение Майера для 1 кило моля газа имеет вид
, (1.6)
где 
= 8314 Дж/(кмоль×К) – универсальная газовая постоянная.
Кроме уравнения Майера, изобарная 
и изохорная 
массовые теплоемкости газов связаны между собой через показатель адиабаты k (табл.1):
. (1.7)
Таблица 1.1