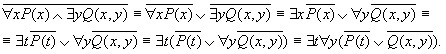Предикаты, так же, как высказывания, принимают два значения истинное и ложное, поэтому к ним применимы все операции логики высказываний. Рассмотрим применение операций логики высказываний к предикатам на примерах одноместных предикатов.
Логические операции
Конъюнкцией двух предикатов А(х) и В(х) называется новый предикат 
, который принимает значение «истина» при тех и только тех значениях х Т, при которых каждый из предикатов принимает значение «истина», и принимает значение «ложь» во всех остальных случаях. Множеством истинности Т предиката А(х) В(х), х Х является пересечение множеств истинности предикатов А(х) – Т1 и В(х) – Т2, т.е. Т= Т1 ∩Т2. Например: А(х): «х – четное число», В(х): «х кратно 3». А(х) В(х) – «х – четное число и х кратно 3». Т.е. предикат «х делится на 6».
Дизъюнкцией двух предикатов А(х) и В(х) называется новый предикат 
, который принимает значение «ложь» при тех и только тех значениях х Т, при которых каждый из предикатов принимает значение «ложь» и принимает значение «истина» во всех остальных случаях. Областью истинности предиката А(х) В(х) является объединение областей истинности предикатов А(х) В(х).
Отрицанием предиката А(х) называется новый предикат, который принимает значение «истина» при всех значениях х Т, при которых предикат А(х) принимает значение «ложь», и принимает значение «ложь», если А(х) принимает значение «истина». Множеством истинности предиката, х Х является дополнение Т' к множеству Т в множестве Х.
Импликацией предикатов А(х) и В(х) называется новый предикат А(х) В(х), который является ложным при тех и только тех значениях х Т, при которых А(х) принимает значение «истина», а В(х) – значение «ложь» и принимает значение «истина» во всех остальных случаях. Читают: «Если А(х), то В(х)». Например. А(х): «Натуральное число х делится на 3». В(х): «Натуральное число х делится на 4», можно составить предикат: «Если натуральное число х делится на 3, то оно делится и на 4». Множеством истинности предиката А(х) В(х) является объединение множества Т2 – истинности предиката В(х) и дополнения к множеству Т1 истинности предиката А(х).
Кванторные операции
Квантор (все-)общности 
Квантор существования 
Квантор существования по переменной x 1
7) Определение. Формула логики предикатов, в которой из операций логики высказываний имеются только конъюнкция, дизъюнкция и отрицание, причем отрицание относится только к элементарным предикатам, называется приведенной формой предиката.
Теорема 1. Для всякого предиката существует равносильная ему приведенная нормальная форма.
Доказательство. Действительно, все операции в данной предикатной формуле можно выразить через конъюнкцию, дизъюнкцию и отрицание (например, в виде ДНФ). Если после этого некоторые отрицания будут относиться к частям формулы, содержащим кванторы, то отрицания можно “снять” с кванторов согласно равносильностям 1 и 2, а “снять” отрицания с конъюнкций и дизъюнкций можно, следуя законам де Моргана. После всех описанных преобразований предикат, очевидно, будет представлен в приведенной форме.
Определение. Предикатная формула вида 
, где Кi – кванторы, хi – различные связанные переменные, а F – предикатная формула без кванторов, находящаяся в приведенной форме, называется предваренной нормальной формой предиката.
Теорема 2. Для всякого предиката существует равносильная ему предваренная нормальная форма.
Доказательство. Согласно теореме 1 можно считать, что предикат уже преобразован в приведенную форму. Если никакая операция навешивания квантора при этом не находится в области действия операций 
и 
, то приведенная форма уже является предваренной нормальной. Поэтому предположим, что описанные ситуации имеют место, и будем называть такие явления (когда какой–либо квантор находится в области действия данной операции или ) беспорядками.
Для данной формулы число беспорядков конечно, так как конечно число символов. Выберем какой-либо беспорядок (скажем, первый слева) и покажем, что путем тождественных преобразований его можно убрать. Возможны два случая:
1) Беспорядок имеет вид: ∀x Р или ∃х Р, где Р – не зависит от х. Тогда ∀х или ∃х можно просто отбросить, поскольку ∀хР ≡ Р и ∃хР ≡ Р.
2) Беспорядок имеет вид: ∀хР(х) или ∃хР(х). Если переменная х еще встречается в формуле, то предварительно сделав замену согласно формулам
∀xP(x) ≡ ∀tP(t), ∃xP(x) ≡ ∃tP(t),
где t – переменная, не встречающаяся в формуле, беспорядок представляется в виде правой части одной из формул 10 – 13. Применяя эти формулы (т.е., заменяя правые части на левые), беспорядок устраняется.
Проделав такие преобразования конечное число раз, все беспорядки будут ликвидированы, что и требовалось доказать.
Пример. Привести к предваренной нормальной форме следующий предикат:
