3.1. Характеристикой среднего значения случайной величины служит математическое ожидание. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: М(Х)= х1р1+ х2р2+…+хnрn.
Свойства М(Х):
1. Математическое ожидание постоянной величины равно самой постоянной: М(С)=С.
2. Математическое ожидание суммы (разности) случайных величин равно сумме (разности) их математических ожиданий: М(Х±У)=М(Х) ± М(У).
3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению их математических ожиданий: М(ХУ)=М(Х)М(У).
4. Постоянный множитель можно выносить за знак математического ожидания: М(СХ)=СМ(Х).
5. Математическое ожидание числа появлений события А в одном испытании равно вероятности этого события р.
ПРИМЕР 4. Найти математическое ожидание случайной величины Х, зная закон ее распределения:
| X | |||
| P | 0,1 | 0,6 | 0,3 |
Решение. Математическое ожидание равно сумме произведений всех возможных значений Х на их вероятности:
М(Х) = 3Ч0,1+5Ч0,6+2Ч0,3=3,9.
ПРИМЕР 5. Доказать, что математическое ожидание числа появлений события А в одном испытании равно вероятности этого события р.
Решение. Случайная величина Х – число появлений события А в одном испытании -может принимать только два значения: х1 =1 (событие А наступило) с вероятностью р и х2 =0 (событие А не наступило) с вероятностью q =1- p. Искомое математическое ожидание равно: М(Х) =1× р +0× q = р.
3.2. Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение.
3.2.1. Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D(X)=M[X-M(X)] 2.
Свойства D(Х):
1. Дисперсия есть величина неотрицательная: D(X)³0.
2. Дисперсия постоянной величины равна нулю: D(С)=0.
3. Дисперсия суммы (разности) случайных величин равна сумме их дисперсий: D(Х±У)=D(Х) + D(У).
4. Дисперсия произведения взаимно независимых случайных величин равна произведению их дисперсий: D(ХУ)=D(Х)D(У).
5. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ)=С2D(Х).
6. Дисперсия случайной величины Х равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания: D(X)=M(X2) -[M(X)]2. При расчетах дисперсию удобно вычислять по этой формуле.
3.2.2. Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:
s(X)=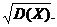 
3.3. Мода Мо – наиболее вероятное значение, т.е. это значение случайной величины, имеющее наибольшую вероятность.
ПРИМЕР 6. Найти дисперсию, среднее квадратическое отклонение и моду дискретной случайной величины Х, заданной рядом распределения:
| X | -5 | |||
| P | 0,4 | 0,3 | 0,1 | 0,2 |
Решение. Найдем математическое ожидание:
М(Х) = -5Ч0,4 + 2Ч0,3 + 3Ч0,1 + 4Ч0,2 = -0,3.
Напишем закон распределения квадрата случайной величины Х 2:
| Х2 | ||||
| P | 0,4 | 0,3 | 0,1 | 0,2 |
Найдем математическое ожидание Х 2:
M(X2) = 25Ч0,4 + 4Ч0,3+ 9Ч0,1+ 16Ч0,2 = 15,3.
Определим дисперсию:
D(X)= M(X2) -[M(X)] 2 = 15,3 -[-0,3] 2 = 15,21.
Найдем среднее квадратическое отклонение:
s(Х)=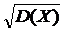 
= 
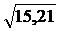= 3,9.
Определим моду: значение случайной величины, имеющее наибольшую вероятность р =0,4, составляет Мо = -5.
4. ЦЕНТРИРОВАННЫЕ И СТАНДАРТНЫЕ СЛУЧАЙНЫЕ
ВЕЛИЧИНЫ
4.1. Пусть случайная величина Х имеет ряд распределения:
| X | х1 | х2 | х3 | … | хn |
| P | р1 | р2 | р3 | … | рn |
Разность между случайной величиной и ее математическим ожиданием называется отклонением или центрированной случайной величиной: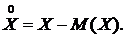 
Ряд распределения центрированной случайной величины имеет вид:
| X -М(Х) | х1 -М(Х) | х2 -М(Х) | … | хn -М(Х) |
| P | р1 | p2 | … | рn |
Свойства центрированной случайной величины:
1. Математическое ожидание отклонения равно 0:
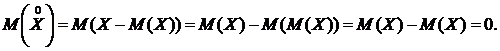
2. Дисперсия отклонения случайной величины Х от ее математического ожидания равна дисперсии самой случайной величины Х:
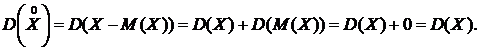
Другими словами, дисперсия случайной величины и дисперсия ее отклонения равны между собой.
4.2. Если отклонение Х - М(Х) разделить на среднее квадратическое отклонение s(Х), то получим безразмерную центрированную случайную величину, которая называется стандартной (нормированной) случайной величиной: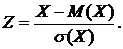 
Свойства стандартной случайной величины:
1. Математическое ожидание стандартной случайной величины равно нулю: M(Z) =0.
2. Дисперсия стандартной случайной величины равна 1: D(Z) =1.
5. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. В лотерее на 100 билетов разыгрываются две вещи, стоимости которых 210 и 60 у.е. Составьте закон распределения суммы выигрыша для лица, имеющего: а) 1 билет, б) 2 билета. Найдите числовые характеристики.
2. Два стрелка стреляют по мишени один раз. Случайная величина Х – число очков, выбиваемых при одном выстреле первым стрелком, – имеет закон распределения:
| Х | |||
| Р | 0,1 | 0,3 | ? |
Случайная величина У – число очков, выбиваемых при одном выстреле вторым стрелком, – имеет закон распределения:
| У | |||
| Р | 0,1 | 0,6 | ? |
Найти закон распределения для случайной величины Z – суммы очков, выбиваемых обоими стрелками. Определить числовые характеристики.
3. Два стрелка стреляют по своей мишени, делая независимо друг от друга по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,7, для второго – 0,8. Случайная величина Х1 – число попаданий первого стрелка, Х2 - число попаданий второго стрелка. Найти закон распределения: а) общего числа попаданий; б) случайной величины Z =3 Х1 - 2 Х2. Определить числовые характеристики общего числа попаданий. Проверить выполнение свойств математического ожидания и дисперсии: M(3X - 2Y)=3M(X) - 2M(Y), D(3X - 2Y)=9D(X)+4D(Y).
4. Случайная величина Х – выручка фирмы – имеет закон распределения:
| Х | |||
| Р | 1/3 | 1/3 | 1/3 |
Случайная величина У – затраты фирмы – имеет закон распределения:
| У | ||
| Р | 0,5 | 0,5 |
Найти закон распределения для случайной величины Z – прибыли фирмы. Определить ее числовые характеристики.
5. Случайные величины Х и У независимы и имеют один и тот же закон распределения:
| Значение | |||
| Р | 0,2 | 0,3 | 0,5 |
Одинаковые ли законы распределения имеют случайные величины 2 Х и Х + У?
6. Доказать, что математическое ожидание стандартной случайной величины равно нулю, а дисперсия равна 1.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какая величина называется случайной?
2. Дайте определение дискретной случайной величины.
3. Что называется законом распределения случайной величины?
4. Что называется рядом распределения дискретной случайной величины?
5. Дайте определение функции распределения вероятностей и перечислите ее свойства.
6. Что называется математическим ожиданием и модой дискретной случайной величины?
7. Сформулируйте свойства математического ожидания.
8. Дайте определение дисперсии дискретной случайной величины.
9. Сформулируйте свойства дисперсии.
10. Что называется средним квадратическим отклонением случайной величины?
11. Какая случайная величина называется центрированной? Сформулируйте ее свойства.
12. Какая случайная величина называется стандартной (нормированной)?
13. Чему равны математическое ожидание и дисперсия стандартной случайной величины?
ЛИТЕРАТУРА
1. Гмурман В.С. Теория вероятностей и математическая статистика. -Изд.7-е, стер. -М.: Высш. шк. 2001.-479 с.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. -Изд.5-е, стер.– М.: Высш. шк. 2001. -400 с.
3. Колде Я.К. Практикум по теории вероятностей и математической статистике. – М.: Высш. шк., 1991. -157 с.
4. Кремер Н.Ш. Теория вероятностей и математическая статистика. -М.: ЮНИТИ-ДАНА, 2001. -543 с.
ОГЛАВЛЕНИЕ
Введение……………………………………………………...............3
1. Основные понятия…………………………………………..........….3
2. Математические операции над случайными величинами....…....7
3. Числовые характеристики дискретных случайных величин..…..10
4. Центрированные и стандартные случайные величины............13
5. Задачи для самостоятельного решения ……………………………14
6. Контрольные вопросы……………………………………….........…16
Литература……………………………………………………........…17
Юлия Борисовна Егорова
Игорь Михайлович Мамонов
ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Методические указания к практическим занятиям
по дисциплине «Математика»
Уч. изд. л. -0,87. Тираж 50 экз.
Издательский центр МАТИ