Правила действий с обыкновенными дробями
Знаменатель обыкновенной дроби показывает на сколько равных частей поделили целое. Числитель показывает сколько таких частей взяли.
целое разделили на 8 равных частей и взяли 5 таких частей
Дробь называется правильной, если числитель меньше знаменателя.
Такая дробь всегда меньше единицы.
, так как 21<32
Если дробь содержит и целую и дробную части, то она называется смешанной.
- 4 целых пять седьмых
Дробь называется неправильной, если её числитель больше знаменателя. Неправильная дробь больше единицы. Её можно представить в виде смешанной и наоборот.
>1, так как 28>15
Чтобы выделить из неправильной дроби целую часть или записать её в смешанном виде нужно:
1. поделить числитель на знаменатель, 28:15=1(ост 13)
2. неполное частное записать в виде целой части 1
3. остаток записать в числителе 13
4. знаменатель оставить прежним 15
Чтобы представить смешанную дробь в виде неправильной, нужно:
1. целую часть умножить на знаменатель 4*7=28
2. к этому прибавить числитель 28+5=33
3. и записать в новом числителе,
4. знаменатель оставить тот же.
= 
Дробь не изменится, если её числитель и знаменатель домножить или поделить на одно и то же число, не равное 0.
домножили на 2
или сразу сократить на 12 
Деление числителя и знаменателя дроби на одно и то же число, отличное от 0, называется сокращением дроби. Чтобы дробь стала несократимой, её делят на наибольший общий делитель НОД, то есть на наибольшее из всех чисел, на которые делятся и числитель и знаменатель.
Если в дроби есть целая часть, то её не домножают и не сокращают
Сравнение обыкновенных дробей.
Из двух дробей с одинаковыми знаменателями меньше та дробь, у которой числитель меньше.
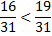
Из двух дробей с одинаковыми числителями меньше та дробь, у которой знаменатель больше.
Если у дробей есть целые части, то сначала сравнивают их.
Если целые части равны, то переходят к сравнению дробных частей
Чтобы сравнить дроби с разными знаменателями, их нужно привести к общему знаменателю.
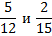
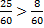значит 
Общий знаменатель будет 60 – это наименьшее из чисел, которые делятся на 12 и 15
Чтобы привести дроби к общему знаменателю, нужно:
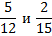
1. Найти общий знаменатель – это наименьшее общее кратное НОК знаменателей,
2. Найти дополнительный множитель для каждой дроби – для этого общий знаменатель делим на знаменатель дроби,
12 нужно домножить на 5, чтобы получить 60, значит первую дробь домножаем на 5
15 нужно домножить на 4, чтобы получить 60, значит вторую дробь домножаем на 4
3. Домножить числитель и знаменатель дроби на найденный дополнительный множитель.
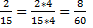
При сложении обыкновенных дробей с одинаковыми знаменателями, знаменатель пишется общий, а числители складываются.
При вычитании обыкновенных дробей с одинаковыми знаменателями, знаменатель пишется общий, а числители вычитаются.
При сложении или вычитании обыкновенных дробей с разными знаменателями, сначала они приводятся к общему знаменателю!, а получившиеся числители складываются или вычитаются.
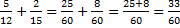эта дробь сократима на 3, значит окончательный ответ 
При сложении смешанных дробей отдельно складываются целые части и дробные части. Если при сложении дробной части получается неправильная дробь, то из неё выделяют целую часть и добавляют её к целой части результата.
При вычитании смешанных дробей нужно:
1. привести дробные части этих дробей к наименьшему общему знаменателю;
2. если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив целую часть на 1;
3. выполнить отдельно вычитание целых частей и вычитание дробных частей.
При умножении обыкновенных дробей нужно записать их под общую черту и перемножить их числители и перемножить их знаменатели. Удобно ещё до умножения сократить получившееся произведение.
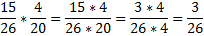
При умножении обыкновенной дроби на целое число, на это число умножается числитель этой дроби, а знаменатель остаётся прежним.
из этой неправильной дроби можно выделить целую часть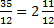 
При умножении смешанных дробе й их обязательно надо привести к неправильному виду!
При делении обыкновенных дробей:
1. Первая дробь остаётся прежней
2. Деление меняется на умножение
3. Вторая дробь заменяется обратной, то есть переворачивается
(числитель и знаменатель меняются местами).
При делении обыкновенной дроби на целое число, на это число умножается знаменатель этой дроби, а числитель остаётся прежним.
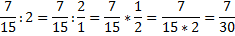
При делении смешанных дробе й их обязательно надо привести к неправильному виду!