Генеральная совокупность и выборка
Статистической совокупностью называется множество однородных предметов или явлений. Отдельные элементы, входящие в совокупность, называются членами статистической совокупности, а общее число членов совокупности – её объемом.
Изменение признака при переходе от одного члена к другому называют его вариацией, а значение признака у данного члена статистической совокупности – его вариантой.
Выборочной совокупностью (или выборкой) называется совокупность случайно отобранных однородных элементов. Генеральной совокупностью называется совокупность всех однородных элементов, из которых производится выборка.
Выборочная и генеральная совокупности, как правило, различаются объемами. Выборка называется репрезентативной, если она достаточно хорошо представляет количественные соотношения генеральной совокупности. Для обеспечения репрезентативности выборки применяют следующие способы отбора: простой отбор (последовательно отбирается первый, случайно попавшийся объект), типический отбор (объекты отбираются пропорционально представительству различных типов объектов в генеральной совокупности), случайный отбор, - например, с помощью таблицы случайных чисел и т. д.
Одной из основных задач статистического анализа является получение по имеющейся выборке достоверных сведений об интересующих исследователя свойствах и параметрах генеральной совокупности.
Основным типом значений переменных в статистике являются количественные переменные.
Вычисление выборочных характеристик
Значения количественных переменных являются числовыми, могут быть упорядочены и для них имеют смысл различные вычисления (например, среднее значение). На обработку количественных переменных ориентировано подавляющее большинство статистических методов.
Первый раздел математической статистики – описательная статистика – предназначен для представления данных в удобном виде и описания информации в терминах математической статистики и теории вероятностей. Для этого используются описательные или дескриптивные характеристики: минимум, максимум, размах, среднее, дисперсия, стандартное отклонение, медиана, квартили, мода.
При анализе конкретного показателя Х в фиксированный момент времени наблюдаемые значения х1,х2, …,хn обычно упорядочивают по неубыванию: 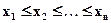 . Разность между максимальным и минимальным значениями СВ Х называется размахом выборки.
. Разность между максимальным и минимальным значениями СВ Х называется размахом выборки.
Если значение xi встречается в выборке ni раз, то число ni называется частотой значения xi, а величина  - относительной частотой значения xi.
- относительной частотой значения xi.
Пусть объем генеральной совокупности равен N. Тогда величина  является генеральной средней. Генеральной дисперсией является величина
является генеральной средней. Генеральной дисперсией является величина 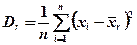 .
.
Генеральным средним квадратическим отклонением является величина  .
.
Так как в реальности чаще всего приходится работать с выборками, то приходится находить выборочные характеристики:
выборочное среднее:
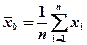

выборочная дисперсия:
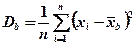
выборочное среднее квадратическое отклонение:
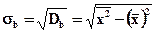
выборочный коэффициент вариации V:
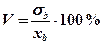 .
.
3.Статистические выводы: оценки и проверка гипотез
Статистические выводы - это заключения о генеральной совокупности на основе выборки, случайно отобранной из генеральной совокупности. Например, анализируется такой показатель как доход (Х) населения некоторого достаточно большого города. Этот анализ может быть осуществлен на основе выборки определенного объема (пусть n=1000). Для выборочных данных определяем средний доход 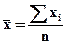 и разброс
и разброс 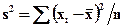 . Далее возникает естественный вопрос: можно ли ожидать, что аналогичные значения будут такими же для всего города? То есть можно ли обобщить результаты, полученные по выборке, на генеральную совокупность. В этом и суть статистических выводов.
. Далее возникает естественный вопрос: можно ли ожидать, что аналогичные значения будут такими же для всего города? То есть можно ли обобщить результаты, полученные по выборке, на генеральную совокупность. В этом и суть статистических выводов.
На основе выборки можно получить лишь оценки параметров генеральной совокупности, так как оценки эти строятся на основе ограниченного набора данных. Естественно, значения оценок могут, изменяется от выборки к выборке. Процесс нахождения оценок по определенному правилу называется оцениванием.
Выделяют два типа оценивания:
- оценивание вида распределения
- оценивание параметров распределения.
В качестве оценки вида распределения можно взять выборочное распределение, а в качестве оценок параметров распределения генеральной совокупности берутся их выборочные оценки.
Различают два вида оценок – точечные и интервальные.
После определения оценок обычно встает вопрос об их качестве и статистической значимости.
Пусть рассматривается генеральная совокупность наблюдаемой СВ Х.
Для оценки ее параметра Θ из генеральной совокупности извлекается выборка объема n: x1,x2,…,xn. На основе этой выборки может быть найдена оценка Θ* параметра Θ.
Точечной оценкой Θ* параметра Θ называется числовое значение этого параметра, полученное по выборке объема n. Например, для нормального распределения параметрами являются математическое ожидание m и среднее квадратическое отклонение σ.
Оценками m и σ могут быть  и
и  соответственно.
соответственно.
Очевидно, что оценка Θ* является функцией от выборки, то есть Θ*=Θ*(х1,х2,…,хп). А так как выборка носит случайный характер, то оценка Θ* является СВ, принимающей различные значения для различных выборок. Любую оценку Θ*=Θ*(х1,х2,…,хп) называют статистической оценкой параметра Θ.
Качество оценок характеризуется следующими основными свойствами: несмещенность, эффективность и состоятельность.
Оценка Θ* называется несмещенной оценкой параметра Θ, если ее математическое ожидание равно оцениваемому параметру: M(Θ*)=Θ.
Оценка Θ* называется эффективной оценкой параметра Θ, если ее дисперсия D(Θ*) меньше дисперсии любой другой выборки объемом n.
Оценка параметра Θ называется асимптотически эффективной, если с увеличением объема выборки ее дисперсия стремится к нулю, то есть 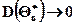 при
при 
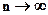 .
.
Оценка Qn называется состоятельной оценкой параметра Θ, если Qn сходится по вероятности к Θ при n ®¥,т.е. для любого e >0 при n ®¥  .
.
Иначе, состоятельной называется такая оценка, которая дает истинное значение при достаточно большом объеме выборки вне зависимости от значений входящих в нее конкретных наблюдений.
Отметим некоторые свойства выборочных оценок.
Доказано, что выборочное среднее 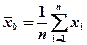 является несмещенной и состоятельной оценкой математического ожидания М(Х) генеральной совокупности.
является несмещенной и состоятельной оценкой математического ожидания М(Х) генеральной совокупности.
Выборочная дисперсия  является смещенной оценкой дисперсии D(X)=σ2. Доказано, что
является смещенной оценкой дисперсии D(X)=σ2. Доказано, что  и это означает, что выборочная дисперсия оценивает генеральную дисперсию неточно.
и это означает, что выборочная дисперсия оценивает генеральную дисперсию неточно.
Поэтому рекомендуется рассматривать исправленную дисперсию
 .
.
Исправленная дисперсия S2 является несмещенной и состоятельной оценкой дисперсии D(X) СВ X.
Необходимо отметить, что при n >30 различие между Db и S2 практически незначимо. Поэтому при большом объеме выборки оценки эти можно считать несмещенными.
Точечная оценка по данным выборки дает оценочное значение соответствующего параметра генеральной совокупности, но ничего не дает для точности и достоверности оценки. Такими оценками являются интервальные оценки. Пусть для оценки параметра Θ генеральной совокупности используется выборка х1,х2, …,хn. Пусть ΘL и ΘU такие значения, что выполняется равенство

Тогда случайный интервал 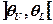 называется доверительным интервалом для оценки параметра Θ с мерой надежности
называется доверительным интервалом для оценки параметра Θ с мерой надежности 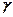 .
.
Другими словами: случайный интервал 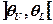 называется доверительным интервалом для оценки параметра Θ с мерой надежности
называется доверительным интервалом для оценки параметра Θ с мерой надежности 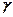 , если с вероятностью
, если с вероятностью 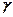 он покрывает оцениваемый параметр.
он покрывает оцениваемый параметр.
По смыслу определения надежности 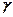 следует брать близким к единице. На практике
следует брать близким к единице. На практике 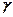 часто принимают обычно равной 0,9; 0,95 или 0,99).
часто принимают обычно равной 0,9; 0,95 или 0,99).
Длина интервала есть случайная величина, зависящая от выборки (х1, х2, …,хn). Случайно и положение интервала на числовой оси  . Интервал обычно симметричен относительно точечной оценки параметра Θ*
. Интервал обычно симметричен относительно точечной оценки параметра Θ* 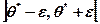 ., для его построения необходимо определить ширину 2 ε или полуширину ε. Вид выражения(формулы) для вычисления полуширины доверительного интервала ε для оценки параметра Θ зависит от того какая предварительная информация о распределении известна. Так, для оценки
., для его построения необходимо определить ширину 2 ε или полуширину ε. Вид выражения(формулы) для вычисления полуширины доверительного интервала ε для оценки параметра Θ зависит от того какая предварительная информация о распределении известна. Так, для оценки  при неизвестном σ из нормально распределениой с законом
при неизвестном σ из нормально распределениой с законом 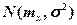 генеральной совокупности Выражение для доверительного интервала имеет вид:
генеральной совокупности Выражение для доверительного интервала имеет вид:
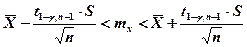
где S –исправленное среднеквадратичное отклонение случайной величины Х, вычисленное по выборке (х1, х2, …,хn), таким образом полуширина равна 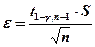 .
.
К пункту 1. Точечные оценки числовых характеристик mX, DX, sX, моды и медианы.
Мода – это наиболее часто встречающееся значение признака в данном ряду распределения. Для дискретных вариационных рядов мода определяется как значение признака с наибольшей частотой. В случае непрерывной вариации мода может быть определена как значение признака, которому отвечает наибольшая плотность распределения частости.
Если 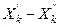 - модальный интервал, т.е. интервал, которому соответствует наибольшая частота Mk, а интервалы вариационного ряда имеют постоянную ширину h, то мода признака вычисляется по формуле
- модальный интервал, т.е. интервал, которому соответствует наибольшая частота Mk, а интервалы вариационного ряда имеют постоянную ширину h, то мода признака вычисляется по формуле
 , (6)
, (6)
где mk-1 и mk+1 – частоты, находящиеся в соответствии с интервалами, предшествующим модальному и следующим за ним.
Если распределение имеет несколько мод, то говорят, что оно мультимодально или многомодально (имеет два или более «пика»).
Медианой МеХ называется значение признака, относительно которого статистическая совокупность делится на две равные по объему части, причем в одной из них содержатся члены, у которых значения признака не больше, а в другой – члены со значениями признака не меньше, чем МеХ.
Если распределение интервальное, то сначала находят так называемый медианный интерва л  , номер которого вычисляют из неравенств
, номер которого вычисляют из неравенств
 ,
, 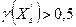 (7)
(7)
где  - накопленная частота в точке х. При предположении, что в медианном интервале признак распределен равномерно, медиана признака Х определяется по формуле:
- накопленная частота в точке х. При предположении, что в медианном интервале признак распределен равномерно, медиана признака Х определяется по формуле:
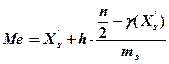
, где h – ширина s -го интервала, ms – частота s –го интервала.
Ассиметрия – это свойство распределения выборки, которое характеризует несимметричность распределения СВ. На практике симметричные распределения встречаются редко и чтобы выявить и оценить степень асимметрии, вводят следующую меру:
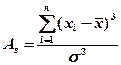 , (4)
, (4)
Пределы значений  от
от 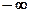 до
до 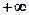 При
При 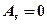 распределение симметрично:
распределение симметрично: 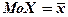 . При положительной асимметрии
. При положительной асимметрии 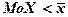 ; при отрицательной
; при отрицательной 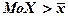
Эксцесс – это мера крутости кривой распределения.
Эксцесс равен:
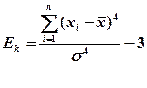 (5)
(5)
Значения  лежат в открытом интервале
лежат в открытом интервале  . Если
. Если 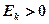 , то кривая распределения имеет более острую вершину, чем нормальное и распределение будет островершинным. Если
, то кривая распределения имеет более острую вершину, чем нормальное и распределение будет островершинным. Если 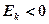 то кривая распределения имеет более плоскую вершину, чем нормальное и распределение будет плосковершинным.
то кривая распределения имеет более плоскую вершину, чем нормальное и распределение будет плосковершинным.
Для нормального распределения  ,
, 
 .
.