Алгоритм симплекс-метода
Теперь мы в состоянии сформулировать алгоритм симплекс-метода для решения задач линейного программирования, заданных в канонической форме.
В первом столбце этой таблицы располагаются обозначения векторов, входящих в базис.
Второй столбец - коэффициенты 
целевой функции, соответствующие векторам, входящим в базис.
Третий столбец - компоненты опорного плана.
В дополнительной строке в этом столбце пишется величина 
. Её легко вычислить перемножая числа из второго столбца и третьего столбца и складывая их.
Далее идут столбцы, соответствующие всем векторам 
, и в этих столбцах записываются координаты этих векторов в рассматриваемом базисе. Заметим, что для векторов, входящих в базис, эти координаты имеют вид (0,0,...,0,1,0,..., 0), где единица стоит в той строке, где находится сам этот базисный вектор.
В дополнительной строке сверху обычно выписывают коэффициенты , соответствующие этим векторам.
В дополнительной строке снизу пишутся величины 
, вычисляемые по формулам:
.
Заметим, что для векторов, входящих в базис, эти разности всегда равны нулю.
Далее идут следующие этапы, связанные с преобразованием этой таблицы. При ручном счете каждый раз эту таблицу лучше переписывать заново, при счете на ЭВМ (который, естественно, всегда используется при решении практических, а не учебных задач), эта таблица просто преобразуется в памяти ЭВМ.
Этап 1
Просматривается дополнительная строка снизу, где записаны разности.
Если все эти разности  ,
| то план является оптимальным |
Этап 2
Если есть столбцы, где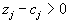 
, то выбирается столбец с максимальным значением этой разности. Индекс j определит вектор, вводимый в базис.
Пусть 
, то есть в базис надо вводить вектор 
. Назовем столбец, соответствующий этому вектору, направляющим столбцом. В дальнейшем мы будем направляющий столбец помечать символом 
.
Этап 3
Просматривается столбец, соответствующий этому вектору. Если все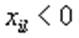 
, то значения целевой функции неограничены снизу. Если есть, 
то находятся
где просматриваются лишь те дроби  ,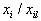
| для которых 
|
Пусть этот минимум достигается для вектора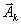 
. Тогда именно вектор 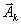подлежит выводу из базиса. Строка, соответствующая этому вектору, называется направляющей строкой. В дальнейшем в примерах мы будем
помечать ее символом  .
|
Этап 4
После того, как определены направляющие столбец и строка, начинает заполняться новая симплекс-таблица, в которой на месте направляющей
| строки будет стоять вектор .
|
Обычно заполнение этой новой таблицы начинается именно с направляющей строки. В качестве компоненты опорного плана туда
пишется величина  , то есть
|
.
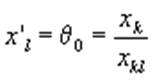Остальные элементы этой строки заполняются величинами
.
Обратите внимание на особую роль элемента 
, стоящего на пересечении направляющей строки и направляющего столбца. Именно на него делятся все бывшие элементы направляющей строки. На месте бывшего элемента автоматически появляется единица.
Написанные выше формулы для пересчета элементов направляющей строки можно записать следующим правилом:
.
Этап 5
Далее начинается пересчет всех остальных строк таблицы, включая и дополнительную нижнюю строку по формулам: для компонент плана
;