Перечень элементов содержания, проверяемых на основном государственном экзамене по ФИЗИКЕ в рамках раздела «Кинематика» (выдержка из кодификатора 2016 г.)
В первом и втором столбцах таблицы указаны коды содержательных блоков, на которые разбит учебный курс. В первом столбце жирным шрифтом обозначены коды разделов (крупных содержательных блоков). Во втором столбце указан код элемента содержания, для проверки которого создаются тестовые задания.
| КОД | Элементы содержания, проверяемые заданиями КИМ | |
| МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ | ||
| 1.1 | Механическое движение. Траектория. Путь. Перемещение | |
| 1.2 | Равномерное прямолинейное движение | |
| 1.3 | Скорость | |
| 1.4 | Ускорение | |
| 1.5 | Равноускоренное прямолинейное движение |
Теория.
Формулы
Автор данного пособия считает, что для решения любой задачи в рамках раздела «Кинематика. Прямолинейное движение» в 9 классе достаточно знать следующие формулы:
| ОБЯЗАТЕЛЬНЫЕ | |
| Скорость в момент времени t |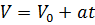 
|
| Путь, пройденный телом к моменту времени t |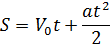 
|
| Дополнительные формулы, которые позволяют многие задачи решить в одно действие – вытекают из обязательных формул. | |
| Ускорение |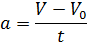 
|
Путь, пройденный телом, если известна начальная и конечная скорость, а также ускорение S(V,V0,  )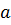
| 
|
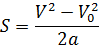
Путь, пройденный телом, если известна начальная и конечная скорость, а также время движения S(V,V0,  )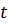
| 
|
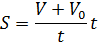
Следует обратить внимание учащихся на тот факт, что при использовании данных формул крайне важно учитывать ЗНАК СКОРЕНИЯ: если тело увеличивает скорость (тело разгоняется), то ускорение в выше указанных формулах остается со знаком «+», если же скорость уменьшается (тело тормозит) – ускорение берется со знаком минус «-».
| ОБЯЗАТЕЛЬНЫЕ | |
| Скорость в момент времени t |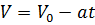 
|
| Путь, пройденный телом к моменту времени t |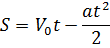 
|
| Дополнительные формулы, которые позволяют многие задачи решить в одно действие – вытекают из обязательных формул. | |
| Путь, пройденный телом, если известна начальная и конечная скорость, а также ускорение S(V,V0, )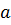
| 
|
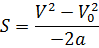
Графики зависимости:
| 1 - равноускоренное движение с начальной скоростью (тело разгоняется) 2 равномерное движение 3 равноускоренное движение без начальной скорости (тело разгоняется) 4 равноускоренное движение (тело тормозит) |
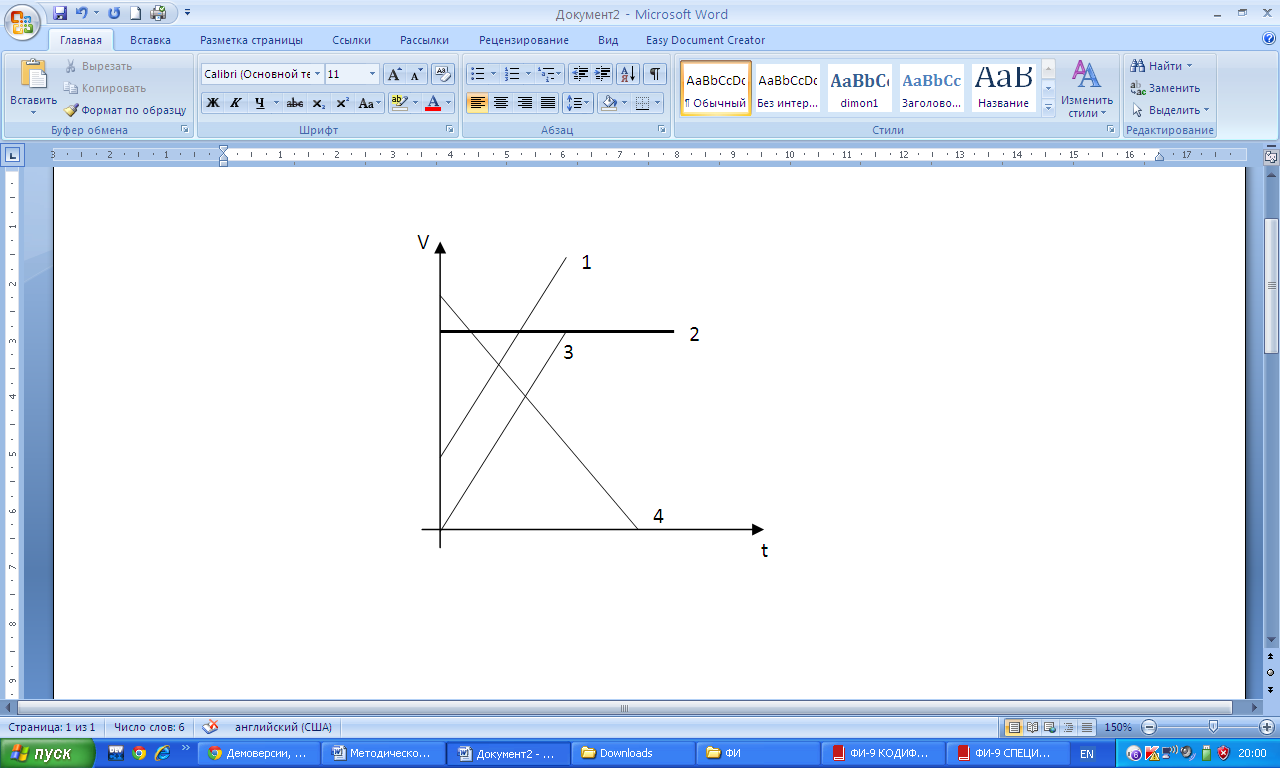
2. Vх=Vх(t) зависимость проекции скорости тела от времени
Следует обратить внимание учеников на отличие графиков зависимости скорости от времени и проекции скорости от времени. Как правило, скорость не может быть отрицательной, а проекция скорости вполне может принимать и отрицательные значения. Необходимо выработать в учениках понимание того, что отрицательная проекция скорости свидетельствует о том, что тело движется в противоположном направлении по отношению к выбранному направлению, или как чаще говорят «тело движется против оси Х». А чтобы понять, как изменяется скорость (разгоняется тело или тормозит) необходимо смотреть именно на изменение модуля скорости.
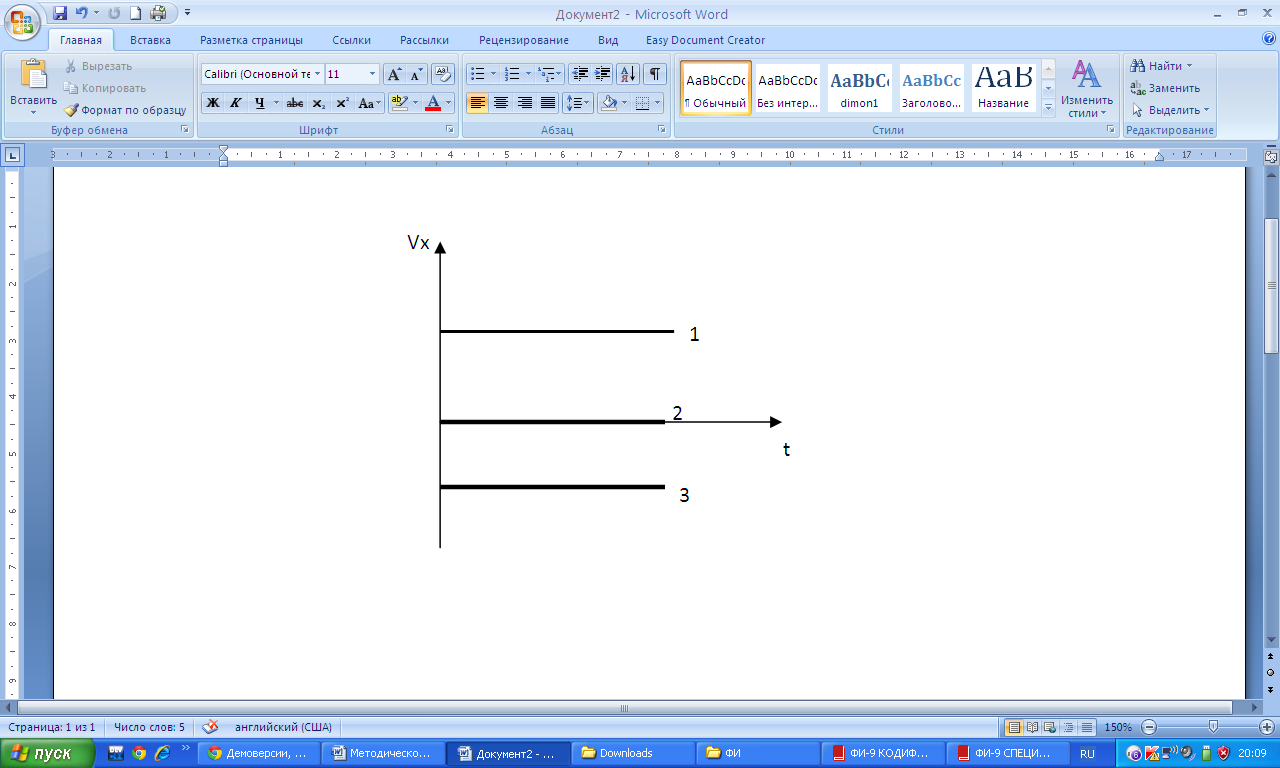
| Все три графика относятся к равномерному движению 1. Равномерное движение вдоль оси ОХ (т.к. проекция скорости положительна) 2. Скорость тела все время равна 0 (тело неподвижно) 3. Равномерное движение против оси ОХ (т.к. проекция скорости отрицательна) |
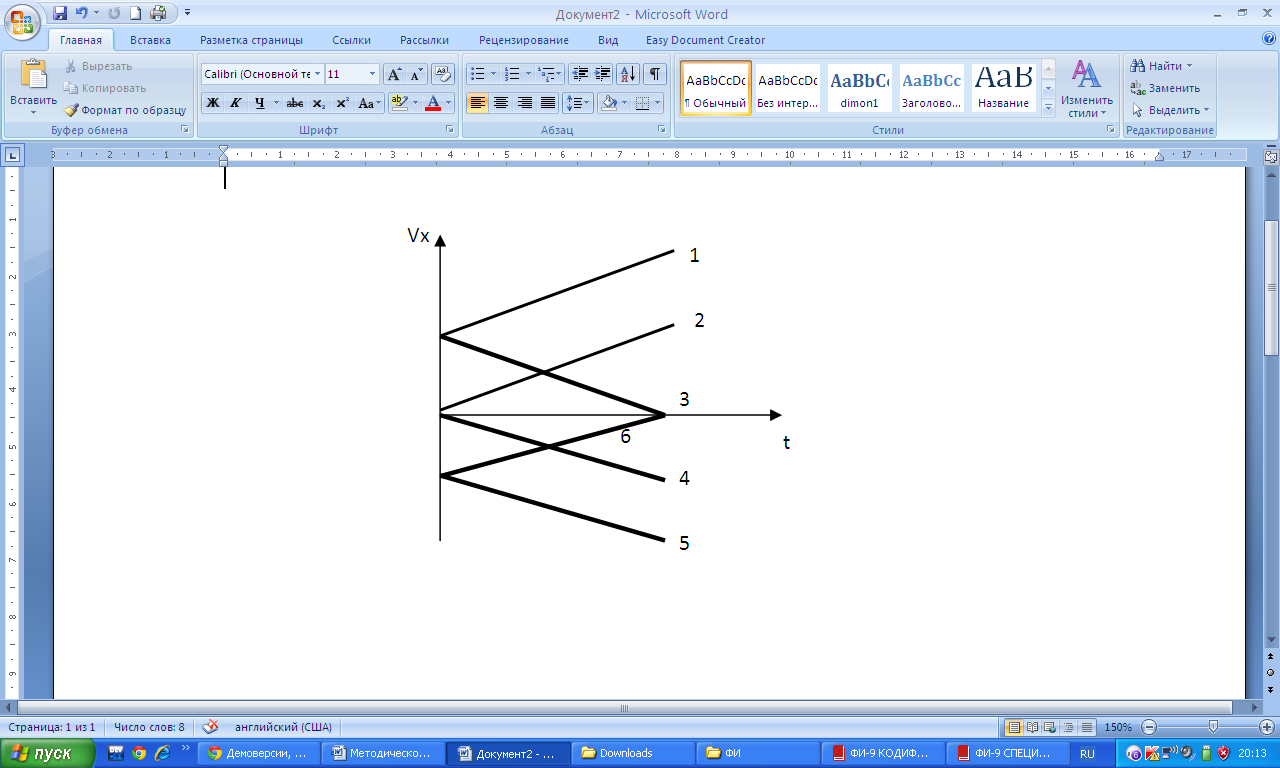
| Все графики выражают зависимость проекции скорости от времени при равноускоренном движении 1. Равноускоренное движение с начальной скоростью вдоль оси (тело разгоняется) 2. Равноускоренное движение без начальной скорости вдоль оси (тело разгоняется) 3 Равноускоренное движение с начальной скоростью вдоль оси (тело тормозит) 4. Равноускоренное движение без начальной скорости против оси (тело разгоняется) 5. Равноускоренное движение с начальной скоростью против оси (тело разгоняется) 5. Равноускоренное движение с начальной скоростью против оси (тело тормозит) |
3. x=x(t) зависимость координаты от времени.
Здесь следует обратить внимание, что внешне похожие графики, например, горизонтальная прямая, в разных зависимостях выражают разное движение. Так в зависимости скорости от времени горизонтальная прямая выражает равномерное движение, а в зависимости координаты от времени такая же прямая выражает тот факт, что тело неподвижно. Конечно, необходимо добиваться не механического запоминания формы графиков в разных зависимостях, а именно осознанное понимание принципа получения графика. Для этого предназначена серия практических заданий, которые будут приведены ниже.
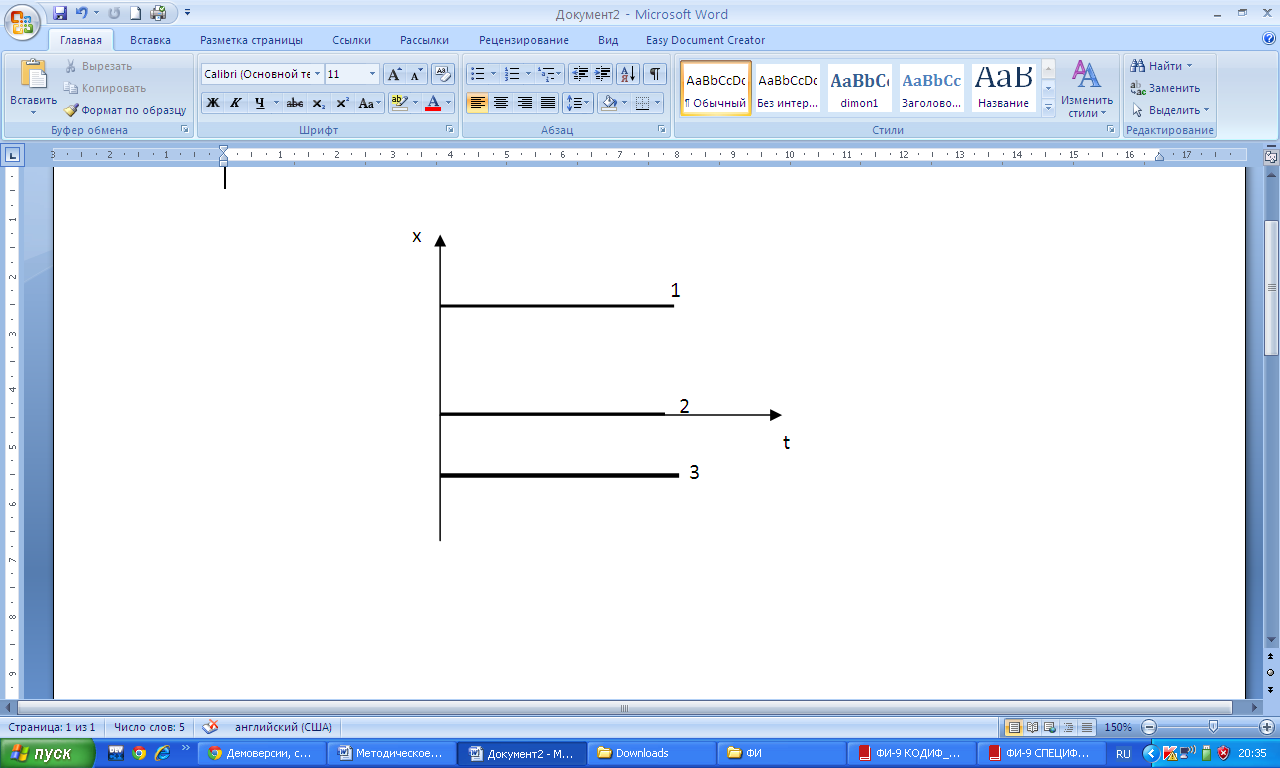
| Все графики выражают состояние покоя т.к. координата тела с течением времени не изменяется 1. Тело неподвижно и находится в точке с положительной координатой 2. Тело неподвижно и находится в начале системы отсчета (т.к. координата все время равна 0) 3 Тело неподвижно и находится в точке с отрицательной координатой |
Следующие ниже графики выражают равномерное движение. Опять необходимо обратить внимание на то, что в системах зависимости скорости от времени подобные графики описывают движение равноускоренное, а в зависимостях координаты от времени это равномерное движение.
Учащимся с достаточно хорошей математической подготовкой можно объяснить этот факт тем, что зависимость координаты от времени при равномерном движении выражается формулой: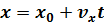 
, а график любой прямой в математике, выражается зависимостью 
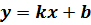т.е. линейной функцией. Разница в том, что первая формула выражает зависимость от времени (t), а вторая формула зависимость просто от х. Но обе переменные (t и х) стоят в первой степени, поэтому зависимость получается линейная, что соответствует графику прямой. Этот факт станет особенной важным, когда учащимся придется объяснять зависимость координаты от времени при равноускоренном движении, где время t уже стоит во второй степени, что соответствует квадратичной функции.
Учащимся без математической подготовки необходимо уделить больше внимания на данные задания на примере решения задач, чтобы за счет большого количества решенных заданий у них выработалось механическое умение определять вид движения.
| Все графики выражают зависимость координаты от времени при равномерном движении 1. Равномерное движение вдоль оси Х из точки с положительной координатой 2. Равномерное движение вдоль оси Х из начала системы отсчета (из точки с координатой 0) 3 Равномерное движение против оси Х от положительной координаты к 0 4. Равномерное движение против оси Х из точки с координатой 0. 5. Равномерное движение против оси Х из точки с отрицательной координатой 6. Равномерное движение вдоль оси Х из точки с отрицательной координатой к точке с координатой 0 |
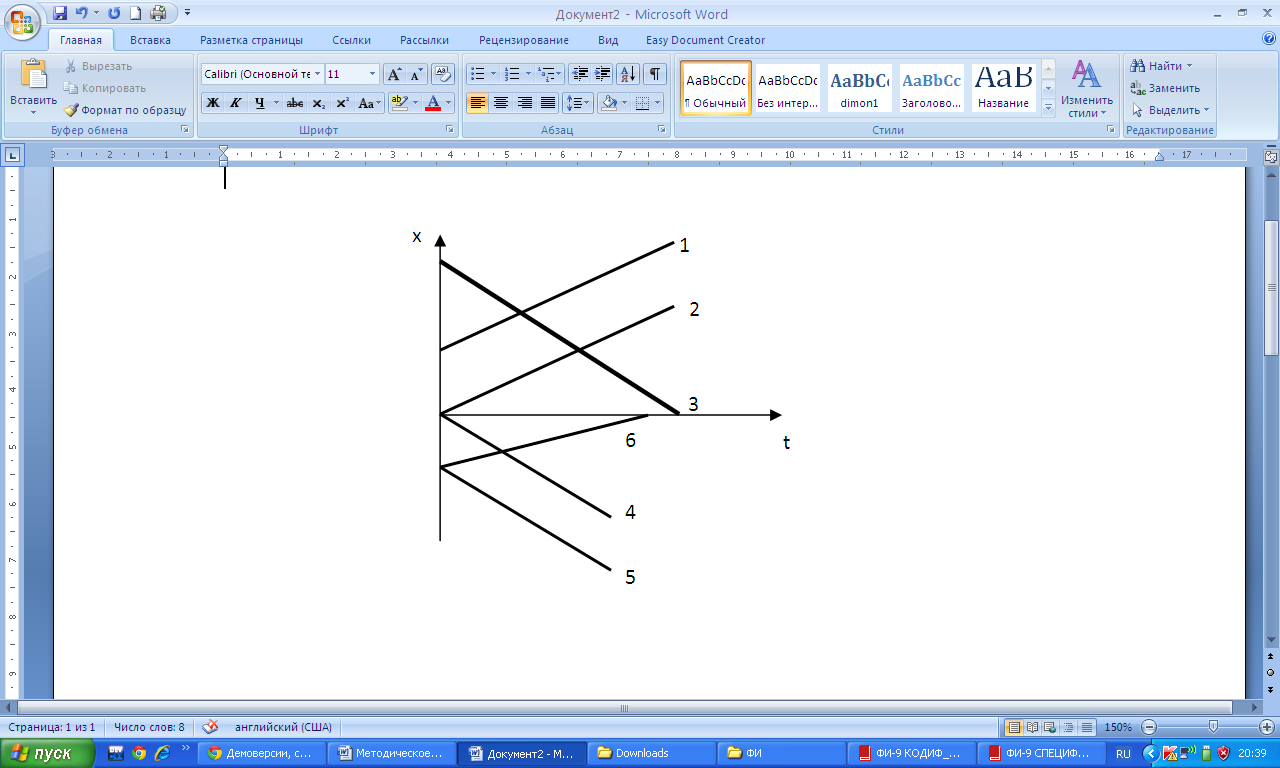
Следующие графики выражают зависимость координаты от времени для равноускоренного движения. Как уже было сказано выше, необходимо добиваться того, чтобы ученики понимали причину того, что в данном случае графиком является парабола т.е. квадратичная функция. Достаточно напомнить, что в формуле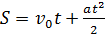 
переменная t находится в квадрате.
| Все графики выражают зависимость координаты от времени при равноускоренном движении из одной точки (с координатой 0) 1. Движении с положительным ускорением (тело разгоняется) 2. Движение с отрицательным ускорением (тело замедляется) |
| Все графики выражают зависимость координаты от времени при равноускоренном движении из одной точки (с координатой 0) против оси т.к. значение координаты «уходит» в область отрицательных значений 1. Движение с замедлением 2. Движении с разгоном |
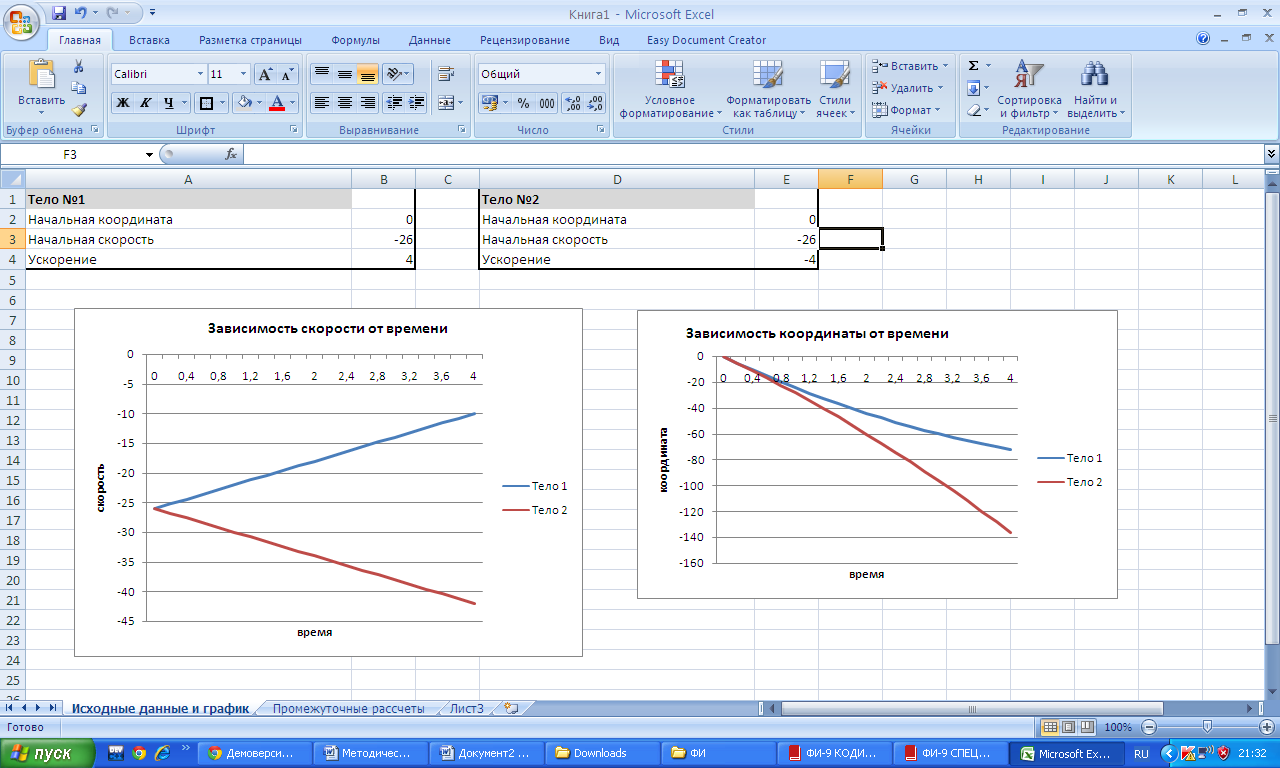
Конечно, графики квадратичной функции вызывают наибольшие затруднения, но как правило для успешного выполнения задания по данному разделу достаточно уметь внешне отличить линейную зависимость – т.е. прямую (равномерное движение) от квадратичной – параболы (равноускоренного движения)
| Если исходить из выше изложенных соображений, то данные графики отражают следующее. 1. Тело движется равноускоренно с положительным ускорением (в 9 классе можно считать, что тело разгоняется) 2. Ускорение равно 0, т.е. движение равномерное. Следует обратить внимание, на то, что нулевое ускорение не означает факт того, что тело неподвижно. Тело может как двигаться равномерно, так и оставаться неподвижным. 3. Ускорение тела отрицательно (в 9 классе можно считать, что тело тормозит) 4.Любая прямая не параллельная оси t выражает общий случай ускоренного движения. Следует обратить внимание, именно на факт того, что подобный график НЕ выражает РАВНОУСКОРЕННОНОЕ движение и не рассматривается в школьном курсе. |
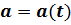– зависимость ускорения от времени. Но, наверное, более верно говорить о зависимости проекции ускорения от времени, а стоит ли делать акцент на этом моменте в 9 классе, как правило, решает сам учитель. Все зависит от того, насколько широко применяется на уроках физики понятие «проекции». Обычно учащимся 9 класса достаточно знать, что если ускорение положительно, то тело разгоняется, если ускорение отрицательно – то тело тормозит. Такая методика, например, применяется в учебники Генденльштейна ….Хотя это утверждение, конечно не всегда является верным, но я думаю, что заострять внимание учеников на подобном противоречии в 9 классе не следует.
Практические задания
Начать отрабатывать данные задания необходимо с заданий, в которых предлагается ученикам самостоятельно построить графики подобные тем, что мы рассмотрели выше. Строить графики лучше на примере конкретных задач с конкретными числами, каждый раз описывая данные графики и их участки. После выполнения подобных задач у учеников должно сформироваться понимание функциональной зависимости скорости, координаты и ускорения от времени.
1. Автомобиль разгоняется с места с ускорением 2 м/с2. Построить график зависимости скорости автомобиля от времени.
Следует перед построением графика оговаривать следующие вопросы:
· Что мы знаем о направлении движения автомобиля? – следует обратить внимание, что раз отдельно о направлении тела ничего в задаче не сказано, можно по умолчанию, т.е. отдельно не оговаривая считать, что автомобиль (или тело) движется вдоль положительного направления оси Х. Конечно, при построении графиков зависимости скорости от времени это значения не имеет, но при построении уже проекции скорости от времени, это имеет важное значение и необходимо сразу приучаться обращать внимание на данный момент.
· Что мы знаем о начальной скорости? – такие фразы как «разгоняется с места», «изначально неподвижное», «покоящееся» говорит о том, что начальная скорость тела была 0.
· В каком временном интервале необходимо строить график? – раз в задаче не указаны конкретные временные границы, то мы сами выбираем временной интервал. Следует отдельно упомянуть о количестве точек необходимом для построения графика. Когда ученики достаточно твердо усвоят, что графиком зависимости скорости от времени при равноускоренном движении является прямая, а для построения прямой достаточно двух значений, то ответ становится очевидным. Но в первых задачах необходимо брать не менее 4х точек, чтобы ученики самостоятельно убедились в справедливости утверждения «что графиком зависимости скорости от времени при равноускоренном движении является прямая»
Образец выполнения задания.
Строим таблицу, в которую будем вносить значения.
| t | ||||
| V |
Запишем формулу (функцию), которая выражает зависимость искомой величины от времени (в данном случае скорости от времени). Сначала в общем виде, а затем с конкретными числами (данными из задачи).
V=V0+at; V=0+2t; V=2t
Произвольно берем значения времени t. Целесообразно первым значением брать начальный момент времени, т.е. 0. Дальнейшее значение времени t берем из соображений удобного расчета и по выше записанной формуле рассчитываем скорость в данный момент времени.
| t | 0,5 | 1,5 | ||
| V |
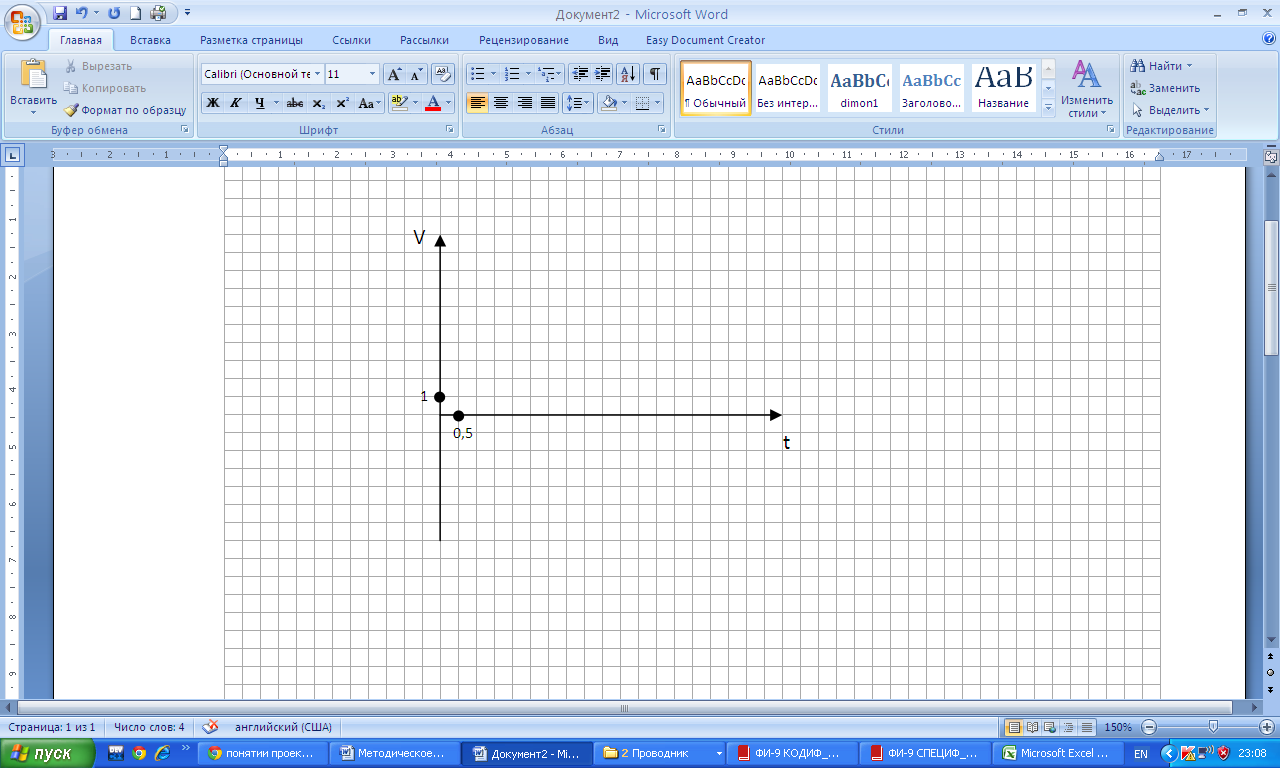
Чертим систему координат, отмечаем единичные отрезки в «удобном» для конкретной задачи.
По таблице отмечаем точки на графике и соединяем прямой.
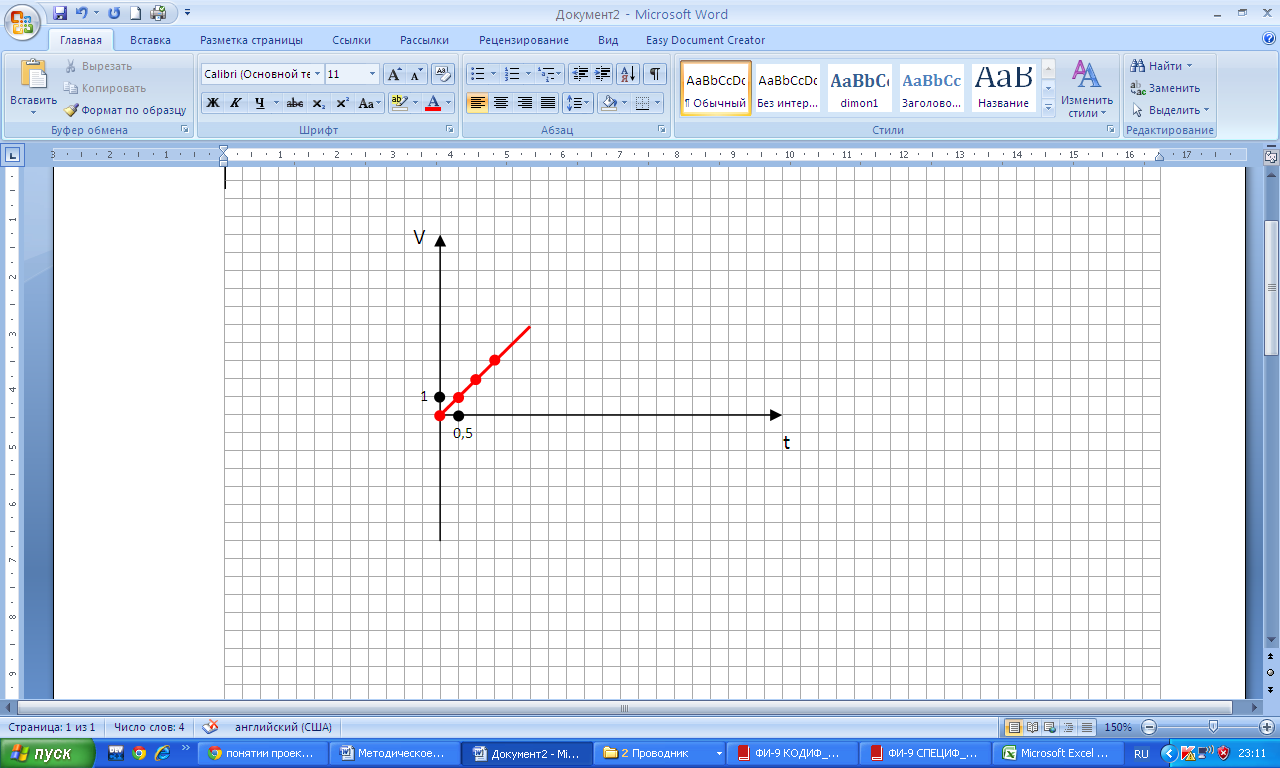
2. Автомобиль имея скорость 36 км/ч начал разгоняться с ускорением 2 м/с2. Построить график зависимости скорости от времени.
Единственным отличием этой задачи от предыдущей является лишь наличие начальной скорости. Конечно, необходимо помнить, о том, что все данные должны быть приведены к одной системе. В данной задаче целесообразно привести начальную скорость в [м/с]. Целесообразно сравнить полученный график с предыдущим.
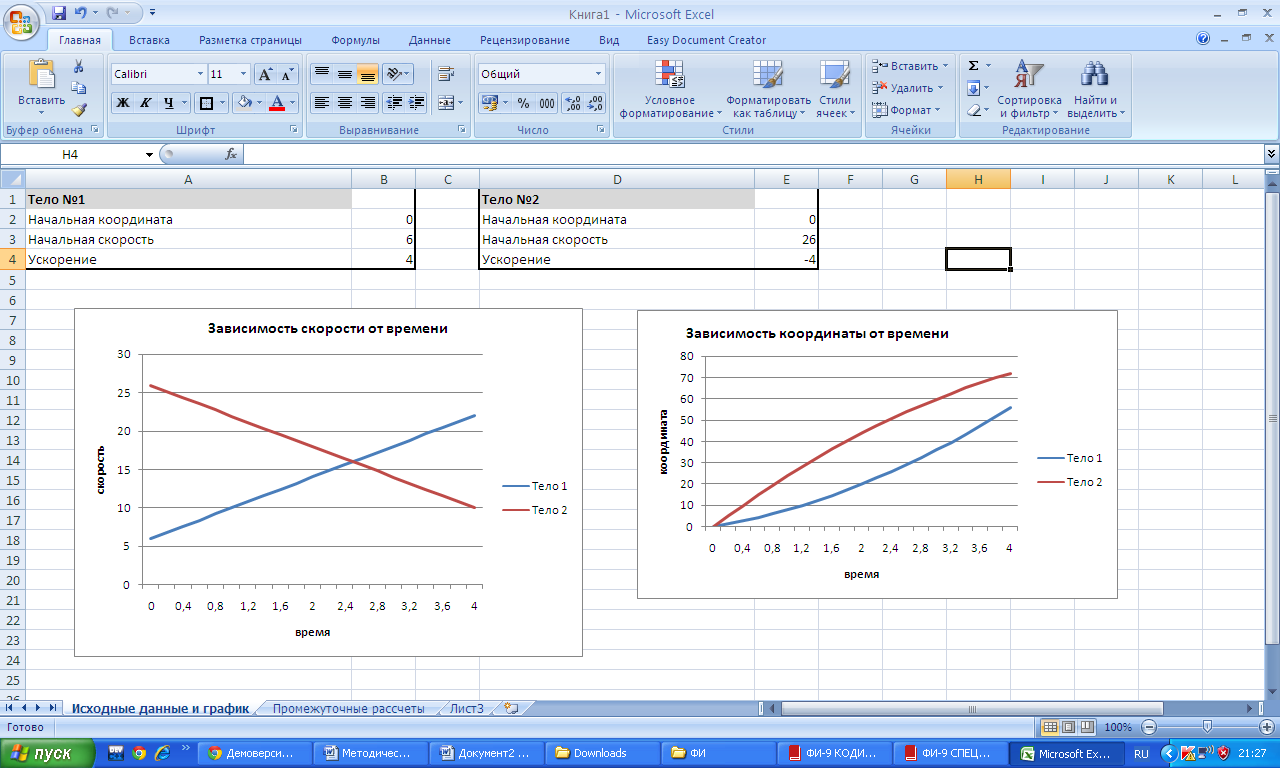
3. Грузовой а втомобиль (тело 1) имея скорость 36 км/ч начал разгоняться с ускорением 2 м/с2, а легковой (тело 2) имея ту же скорость начал разгоняться с ускорением 4 м/с2. Построить график зависимости скорости от времени в одной системе координат.
| Следует обратить внимание, как на графике отражается тот факт, что у второго автомобиля ускорение больше. |
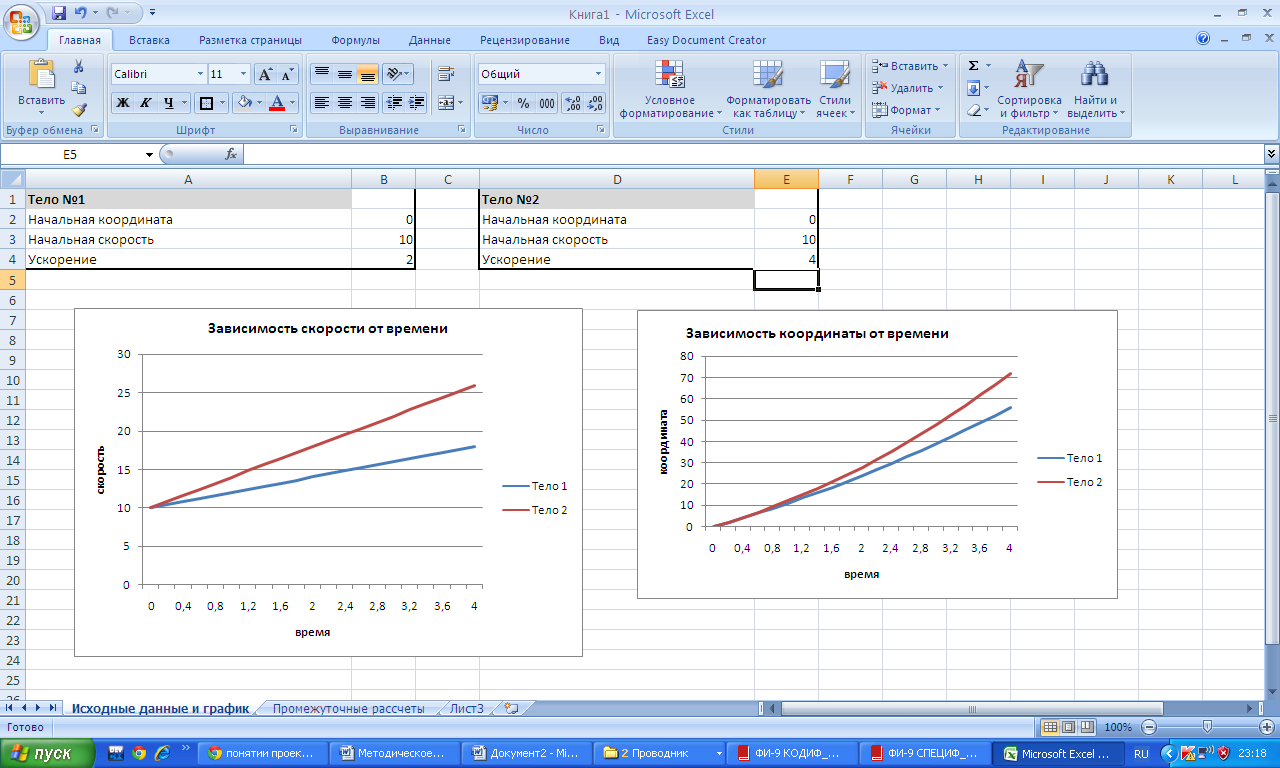
4. Два автомобиля, двигаясь со скоростью 72 км/ч., начали изменять свою скорость. Первый начал разгоняться с ускорением 2 м/с2 а второй тормозить с таким же ускорением. Построить график зависимости скорости от времени в одной системе координат.
Примерный график:
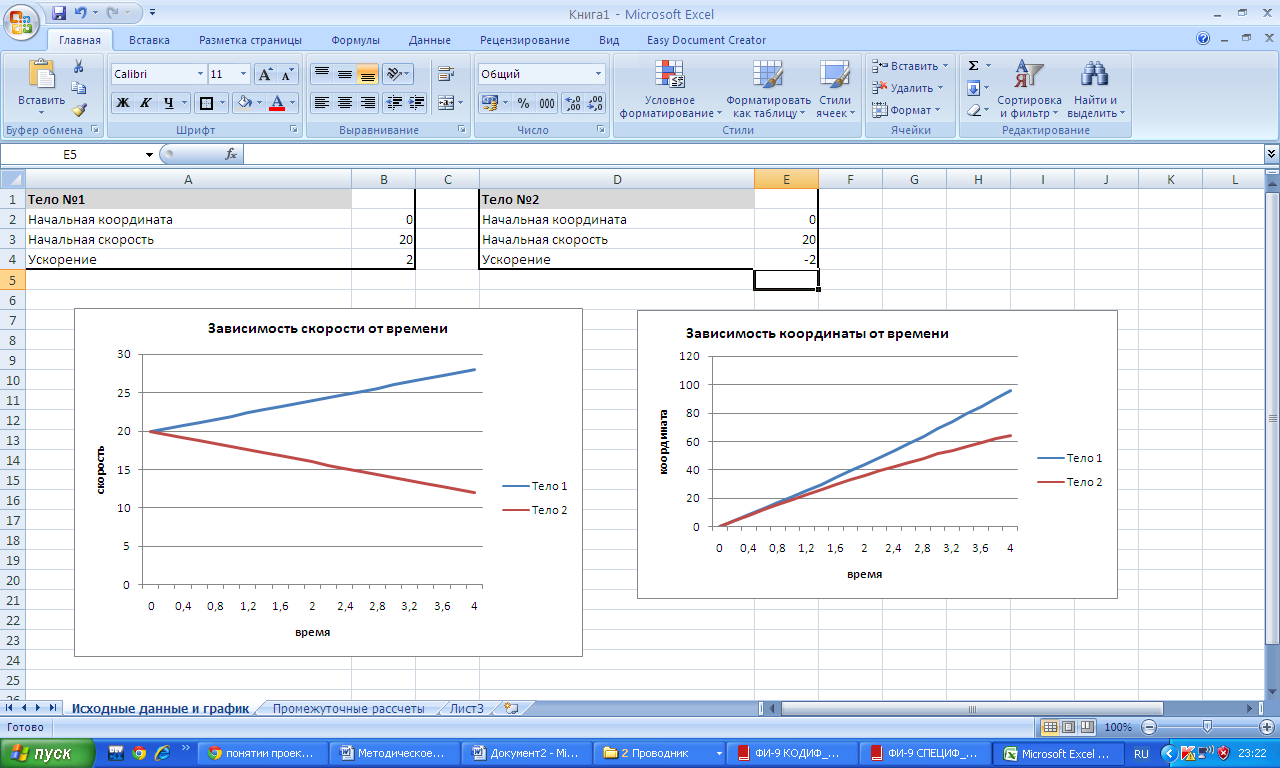
5. Автомобиль двигаясь с места, разгонялся с ускорением 1 м/с2 в течении 10 с, а затем двигался равномерно в течении 8 секунд, а затем остановился за две секунды. Построить график зависимости скорости от времени.
В данной задаче целесообразно рассуждать, опираясь на физический смысл ускорения и равномерного движения. Можно сделать так: строим таблицу, в которой уляжется весь временной диапазон. Сначала тело двигалось 10 с разгоняясь, затем 8 секунд равномерно, и затем 2 секунды тормозило. Итого 20 секунд.
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| v |
По условию автомобиль разгонялся с места, значит при t=0 скорость v=0
Затем опираясь на физический смысл ускорения (показывает на сколько меняется скорость тела за каждую секунду) выясняем, что скорость автомобиля после 1 секунды разгона станет 1 м/с, затем 2 м/с, 3 м/с, 4 м/с и так далее в 10 секунду скорость стала равна 10 м/с. Теперь вспоминаем смысл равномерного движения (скорость тела не изменяется) – значит и в 11 и в 12 секунду, и так далее в течении 8 секунд (т.е. до 18 секунды включая) скорость будет неизменна и равна 10 м/с. За две последние секунды скорость уменьшилась до нуля и таким образом в 20 секунду скорость стала 0. Обратим внимание, что в данной задаче не важна скорость в 19 секунду. Важно лишь то, что в 18 с скорость была еще 10 м/с а уже в 20 ую секунду скорость стала 0 м/с.
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| v | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 0 |
Строим график по точкам
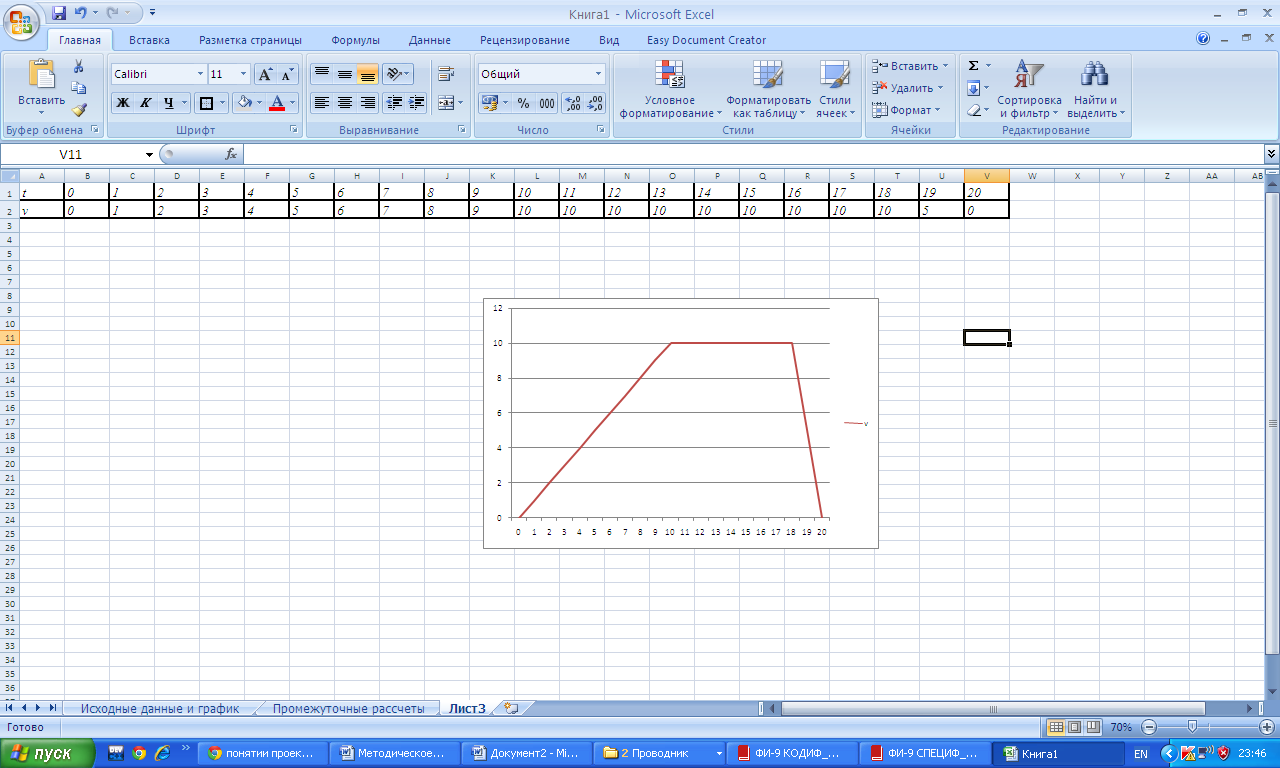
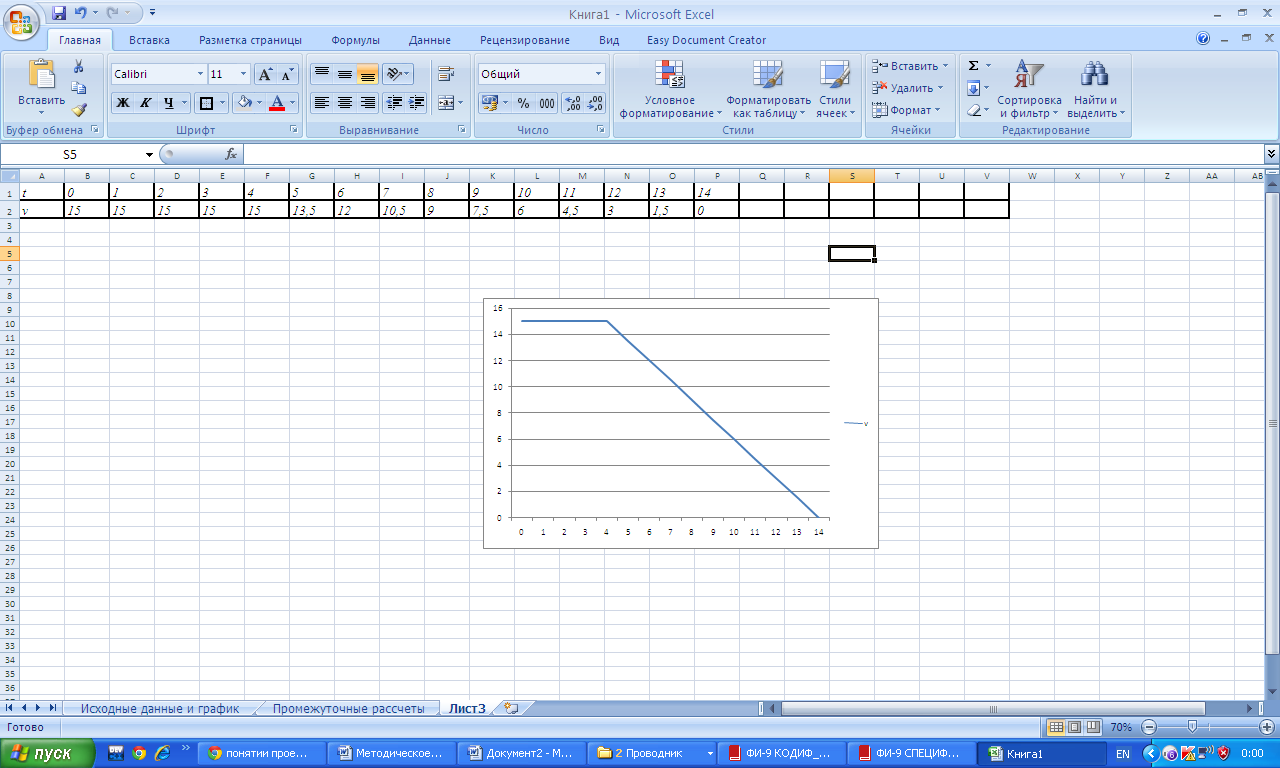
6. Автомобиль двигался со скоростью 15 м/с в течении 4 секунд, а затем начал тормозить с ускорением 1,5 м/с2 до полной остановки. Построить график зависимости скорости от времени.
Принципиально эта задача не отличается от предыдущей, но в ней лучше раскрывается физический смысл ускорения. Строя таблицу, ученик высчитывает скорость в каждый момент времени без использования формулы, а только опираясь на рассуждения и простейшие математические расчеты. Кстати, заведомо не известен момент остановки автомобиля, поэтому таблицу можно взять с «запасом». Кроме того, в начальный момент времени скорость тела отлична от 0.
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| v | 15 | 15 | 15 | 15 | 15 | 13,5 | 12 | 10,5 | 9 | 7,5 | 6 | 4,5 | 3 | 1,5 | 0 |
Примерный график
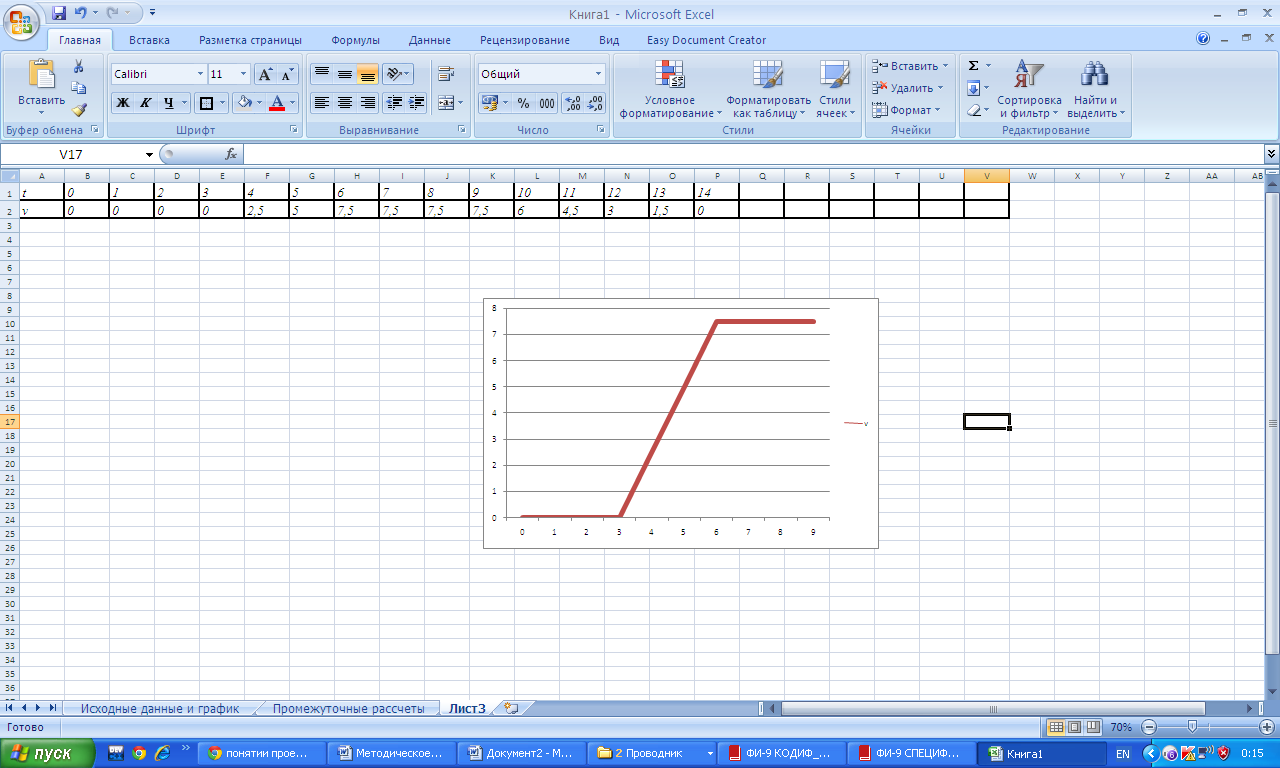
7. Автомобиль стоявший в течении 3 секунд, начал разгонятся с ускорением 2,5 м/с2 в течении следующих 3х секунд, затем продолжил равномерное движение. Построить график зависимости скорости от времени.
Особенностью этой задачи является неподвижность тела в начальный промежуток времени. Рассуждая, что тело с начальной (нулевой) секунды до 3 секунды было неподвижно т.е. имело скорость 0 м/с, затем скорость тела росла каждую секунду на 2.5 м/с в течении 3 секунд, после чего перестала изменяться получаем следующую таблицу. Время окончания выбираем произвольно, но берем хотя бы два три значения после последнего изменения скорости.
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| V | 0 | 0 | 0 | 0 | 2,5 | 5 | 7,5 | 7,5 | 7,5 |
Примерный график
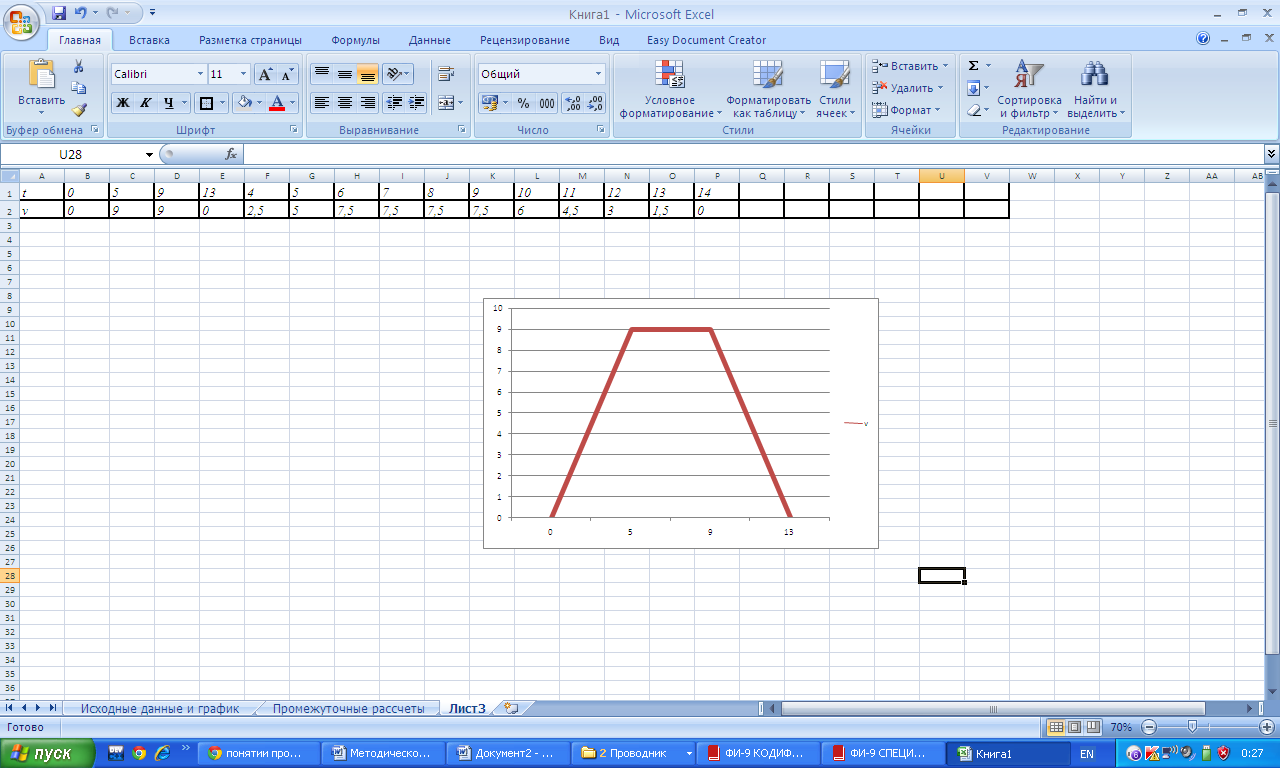
8. Автомобиль разгоняясь с места к 5-ой секунде достиг скорости 9 м/с, затем двигался с постоянной скоростью в течении 4 секунд, после чего затормозил за 4 секунды. Построить график зависимости скорости от времени.
Особенность данной задачи в том, что она не требует расчета промежуточных значений скорости, хотя это можно сделать в качестве тренировки, предварительно рассчитав ускорения, но для построения графика это не является необходимым. Достаточно в таблице взять только те значения времени, о которых идет речь в условии: начальный момент времени t0=0, t1=5, t2=5+4=9, t3=9+4=13
| t | 0 | 5 | 9 | 13 |
| V | 0 | 9 | 9 | 0 |
Примерный график
После того как учащиеся достаточно много построили графики для различных случаев движения, можно рассмотреть обратные задачи, когда график уже дан, и по его виду необходимо описать движение.
| Vx |
| -6 |
| t(c) |
| (м/с) |
Задания подобного типа можно формулировать двумя способами.
Способ1. Описать характер движения на каждом участке. Т.е. ученик должен для каждого временного интервала указать, что происходит со скоростью тела, куда движется тело (вдоль оси ОХ или против неё). Решение можно оформить в виде таблицы
| Временной интервал | Изменение модуля скорости | Направление движения | Знак ускорения |
| 0-5секунды | Увеличивается | Вдоль оси ОХ | Положительный |
| 5-10 секунды | Не изменяется | Вдоль оси ОХ | Равно 0 |
| 10-12 секунды | Уменьшается | Вдоль оси ОХ | Отрицательно |
| 12-16 секунды | Увеличивается | Против оси ОХ | Отрицательно |
| 16-18 секунды | Уменьшается | Против оси ОХ | Положительно |
| 18-19 секунды | Увеличивается | Вдоль оси ОХ | Положительно |
| 19 и далее секунды | Не изменяется | Вдоль оси ОХ | Равно 0 |
Кроме того описание можно дать в произвольной форме: «В начальный момент времени тело было неподвижно, затем оно разгонялось до скорости 10 м/с в течении 5и секунд. Затем двигалось равномерно в течении 5 секунд т.е. до 10 секунды. С 10 секунды тело стало тормозить, продолжая двигаться вдоль оси ОХ, и остановилось в 12 секунду. Начиная с 12 секунды тело начало разгоняться, но двигаясь уже против оси ОХ. К 16 секунде от начала движения тело достигло скорости 6 м/с, при этом продолжало двигаться против оси ОХ (т.к. проекция скорости по прежнему отрицательна). С 16 секунды тело начало тормозить и остановилось в 18 секунду. С 18 секунды скорость начала расти, а ее проекция положительна, следовательно, тело разгоняется вдоль оси ОХ и достигает скорости 3 м/с к 19 секунде после начала движения. С 19 секунды тело движется равномерно вдоль оси ОХ со скоростью 3 м/с»
Способ 2 рассмотрим на втором графике.
10. По графику зависимости скорости от времени описать движение тела.
| t(с) |
| Vx (м/с) |
| -11 |
В таком способе постановки задачи, учащимся предлагается ответить на ряд следующих вопросов:
· В какой или какие интервалы времени тело двигалось равномерно? (С 10 по 12 секунды)
· Какова скорость равномерного движения? (10 м/с)
· В какие интервалы времени тело разгонялось? (c 5 по 10 секунды, с 14 по 16 секунды, с 18 по 20 секунды)
· В какие моменты времени тело двигалось вдоль оси ОХ? (с 0 по 14 секунды, с 18 по 24 секунды)
· В какие моменты времени тело разгонялось, двигаясь против оси ОХ? (с 14 по 16 секунды)
· В какие моменты времени тело останавливалось? (в 5, 14, 18 и 24 секунды)
· Куда по отношению к оси ОХ двигалось тело с 16 по 18 секунду? (с 16 по 18 секунду тело двигалось против оси ОХ, т.к. проекция скорости отрицательна)
· В какие интервалы времени тело тормозило, двигаясь вдоль оси ОХ? (c 0 по 5 секунды, с 12 по 14 секунды, с 20 по 24 секунды)
· Какова максимальная скорость во время всего движения? (11 м/с)
Дополнительно можно попросить учеников указать временной интервал, на котором тело двигалось с максимальным по модулю ускорением. Для получения ответа на поставленный вопрос, учащимся придется рассчитать ускорение на каждом временном интервале. Это задание обычно вызывает сложности в связи с неправильным пониманием смысла t стоящего в знаменатели дроби, определяющей определение ускорения. Рассмотрим пример на следующем графике: определить интервал времени, в котором ускорение максимально по модулю.
| t(с) |
| Vx (м/с) |
| -10 |
Выясняем, что в первые пять секунд тело двигалось с отрицательным ускорением, т.е. «тормозило» от скорости 10 м/с до 0. Если ученики твердо понимают смысл ускорения, то рассуждая, что за 5 секунд тело изменило свою скорость на 10 м/с, то за каждую секунду скорость изменялась на 2 м/с, т.е. ускорение тела -2м/с2.
Если подобные рассуждения вызывают затруднения, то можно предложить использовать формулу: V=V0+at и выразить a: a=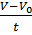 
. Конечно, ученики должны отличать V и V0 и уметь определять их значения из графика. Итак: V- конечная скорость на данном участке пути, V=0;
V0- начальная скорость на данном участке, V0=10;
t- время движения на данном участке, t=5. Подставляем в формулу: a=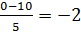 
.
Такие авторы как С.В.Громов предлагают просто ученикам запомнить ряд формул для частных случаев ("Физика. Учебник для 8 класса" С.В. Громов, Москва "Просвщение" 2002):
| Характеристика движения |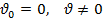 
|
|
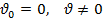
| Ускорение |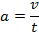 
| 
|
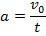
| Время | Время разгона
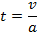
| Время торможения
|
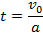
| Скорость | Конечная скорость
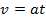
| Начальная скорость
|
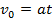
| Пройденный путь | Путь при разгоне
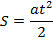
| Путь при торможении
|
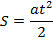
Из таблицы следует, что ускорение в данном случае можно рассчитать просто по формуле: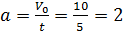 
. На мой взгляд, запоминание всех формул нецелесообразно, т.к. в них просто запутаться, а также эти формулы не учитывают знак ускорения. Итак, на первом участке пути модуль ускорения равен 2м/с2.
Переходим к второму участку графика. Анализируя график, приходим к выводу, что тело разгонялось со скорости 0 м/с до 10 м/с в интервале с 5-ой по 10-ую секунды, т.е. разгон длился всего 5 секунд. Как правило, у некоторых учащихся возникает ошибка с неправильным определением времени t: иногда глядя на график ученики берут время 10 секунд, т.е. берут не интервал времени, а момент времени. Крайне важно обратить внимание, что в качестве t необходимо брать именно интервал времени, в данной задаче 5 секунд. Из формулы V=V0+at получаем ускорение равное 2. Или можно рассуждать, что раз за 5 секунд разгона тело изменило скорость с 0 до 10 м/с, значит, за каждую секунду скорость изменялась на 2 м/с.
Анализируем третий участок графика. Графиком является горизонтальная прямая, следовательно, движение равномерное, ускорение равно 0. Интересно просчитать в данном случае ускорение по формуле: a= 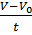. На данном участке графика и начальная и конечная скорость равны 10м/с, интервал времени (движения) равен 2 секундам. Подставляем числа и получаем: 
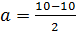=0.
Переходим к четвертому участку графику. Сложность, которая возникает, это определение рассматриваемого временного участка: с одной стороны прямая графика идет без преломлений с 12 до 16 секунды, а с другой стороны на этом участке проекция скорости меняет знак, следовательно, тело меняет направление движения. Что происходим с ускорением на этом участке? Можно просто рассуждать: так как с 12 секунды тело тормозило, значит, ускорение отрицательно. С 14 секунды (на графике не обозначено) тело разгоняется, но с отрицательной проекцией скорости, следовательно, проекция ускорения опять отрицательна. Если подобные рассуждения сложны для учеников, то в 9 классе можно дать как факт, что если прямая графика не искривляется, то ускорение тела неизменно. Таким образом, раз прямая графика не искривляется в интервале с 12 по 16 секунды, значит можно ускорение высчитывать на этом интервале. Используем формулу a= 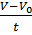, определяем значения скоростей: V=-10, V0=10, интервал времени t=4 секундам (движение с 12 по 16 секунду), подставляем в формулу, получаем:
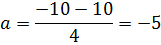
Для пятого участка аналогично определяем V=0, V0=-10, интервал времени с 16 по 18 секунды, т.е. 2 секунды.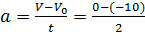 
=5
Обратите внимание, что на участке с 16 по 21 секунды график искривляется, значит, ускорение меняется по модулю и по этой причине его необходимо считать на двух интервалах: с 16 по 18 секунды, и с 18 по 21 секунды.
Шестой участок представлен интервалом с 18 по 21 секунду, т.е. интервал, в котором движется тело равен 3 секундам, начальная скорость на этом интервале V0=0, конечная скорость V равна 8 м/с, делаем расчеты:
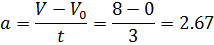
И седьмой участок: V0=8, V=0, интервал времени t=3. Ускорение равно
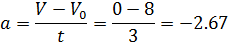
Максимальным по модулю ускорение является в интервале с 12 по 16 секунду.
Следующий тип заданий, которые могут встретиться учащимся при решении задач на графики, обычно сводятся к нахождению пройденного пути по графику зависимости скорости от времени. Конечно, обычно на уроке акцентируется внимание, что путь, пройденный телом, численно равен площади фигуры, ограниченной координатными осями и графиком V(t), но как правило, к моменту сдачи экзамена этот факт забывается, поэтому следует решить несколько задач подобного типа.
| t(с) |
| V(м/с) |
Первым шагом для решения этой простой задачи является выбор формулы, по которой можно рассчитать путь, а для этого необходимо определить вид движения. Предполагается, что к моменту решению этой задачи, учащиеся уже легко определяют вид движения. Итак, вид движения определен – движение равномерное, следовательно, формула для расчета пути имеет вид:
S=vt
| t(с) |
| V(м/с) |
| Путь пройденный телом, числено равен площади заштрихованной фигуры. |
| t(с) |
| Vx(м/с) |
| -3 |
12. Сравнить пути, пройденные первым и вторым телом, за одно и то же время. Графики зависимости проекции скорости от времени для тел даны.
Задача аналогична предыдущей, с разницей в том, что необходимо рассчитать два пути. Скорость тел ученики берут из графиков: V1 =8 м/с, V2=3 м/с.Учащиеся должны помнить, что знак «-» у проекции скорости второго тела означает, только направление движение против оси Х, а при расчете пути достаточно брать модуль скорости. Также у учащихся может возникнуть сложность с выбором времени движения. В задаче явно время движения не дано,поэтому необходимо обратить внимание учеников на произвольный выбор числового значения t. Например, в задаче можно взять время 10 секунд. С учетом скорости тел и произвольно выбранного времени получаем: S1=80 м, S2=30 м. Таким образом, путь пройденный первым телом больше пути второго тела. Но, на примере этого задания намного важнее показать, тот факт, при решении задач на сравнение пройденных путей, вообще не надо делать числовых расчетов, достаточно просто сравнить площади фигур:
| t(с) |
| Vx(м/с) |
| -3 |
| S1 |
| S2 |
| Из графиков видно, что площадь первого заштрихованного прямоугольника больше, чем площадь второй фигуры, следовательно, и путь, пройденный первым телом больше чем путь второго тела. |
| t(с) |
| Vx(м/с) |
13.Определить путь, пройденный автомобилем за 10 секунд, график зависимости скорости от времени которого дан.
При рассуждении, ученики приходят к выводу, что этот график соответствует равноускоренному движению тела без начальной скорости, следовательно, необходима формула:
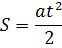
Теперь необходимо рассчитать ускорение: a=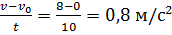 
. После подстановки в формулу расчета пути, получаем: S=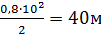 
| t(с) |
| Vx(м/с) |