1) Построить область допустимых решений.
2) Если область допустимых решений является пустым множеством, то задача не имеет решения вследствие несовместности системы ограничений.
3) Если область допустимых решений является непустым множеством, построить вектор-градиент целевой функции.
4) Произвольную линию уровня, имеющую общие точки с ОДР, перемещаем параллельно самой себе до опорной прямой в направлении вектора-градиента (при решении задачи на  ) или в противоположном направлении (при решении задачи на
) или в противоположном направлении (при решении задачи на  ).
).
5) Если при перемещении линии уровня по ОДР в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения вследствие неограниченности целевой функции.
6) Если ЗЛП имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих ОДР и имеющих общие точки с соответствующей опорной прямой. Если целевая функция задачи достигает экстремума в двух вершинах ОДР, то она достигает экстремума также в любой точке, лежащей на отрезке, соединяющем эти две вершины. Задача имеет бесконечное множество оптимальных решений.
7) Вычислить значение целевой функции на оптимальном решении.
Пример 1.6
Решим графически ЗЛП, математическая модель которой составлена в примере 1.3.
 ;
;

Вначале построим ОДР задачи (рис. 1.2). Для этого в системе координат  на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:
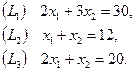

Рис. 1.2
Затем определим, какую полуплоскость определяет соответствующее неравенство, подставив координаты какой-нибудь точки, не лежащей на данной прямой, например (0;0). Ограничения (1.17) означают, что ОДР лежит в I четверти системы координат  . Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет ОДР данной задачи.
. Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет ОДР данной задачи.
Строим вектор-градиент целевой функции  =(5;4).
=(5;4).
Строим произвольную линию уровня, например  , проходящую через начало координат и перемещаем ее параллельно самой себе в направлении вектора
, проходящую через начало координат и перемещаем ее параллельно самой себе в направлении вектора  по ОДР (рис. 1.2). Последняя точка соприкосновения прямой
по ОДР (рис. 1.2). Последняя точка соприкосновения прямой  с ОДР и есть оптимальное решение – это точка С.
с ОДР и есть оптимальное решение – это точка С.
Точка  лежит на пересечении прямых
лежит на пересечении прямых  и
и  . Для определения ее координат необходимо решить систему уравнений:
. Для определения ее координат необходимо решить систему уравнений:

Откуда  . Таким образом,
. Таким образом,  . Подставив значение
. Подставив значение  и
и  в целевую функцию Z, получаем:
в целевую функцию Z, получаем:
 .
.
Таким образом, для того, чтобы получить максимальную прибыль в размере 56 ден. ед., необходимо запланировать выпуск 8 ед. продукции вида П1 и 4 ед. продукции П2.
Пример 1.7
Графическим методом решить ЗЛП:

Решение
Вначале построим ОДР задачи (рис. 1.3). Для этого в системе координат  на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:

Затем определим, какую полуплоскость определяет соответствующее неравенство, подставив координаты какой-нибудь точки, не лежащей на этой прямой. Ограничения  означают, что ОДР лежит в I четверти системы координат
означают, что ОДР лежит в I четверти системы координат  . Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет ОДР данной задачи – это открытая многоугольная область ABCD.
. Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет ОДР данной задачи – это открытая многоугольная область ABCD.
Строим вектор-градиент целевой функции  =(3;6). Берем произвольную линию уровня целевой функции (на рисунке она обозначена пунктирной линией) и перемещаем ее в направлении вектора-градиента до последней точки соприкосновения с ОДР для определения оптимального решения на
=(3;6). Берем произвольную линию уровня целевой функции (на рисунке она обозначена пунктирной линией) и перемещаем ее в направлении вектора-градиента до последней точки соприкосновения с ОДР для определения оптимального решения на 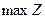 , при этом линия уровня уходит в бесконечность, следовательно, на
, при этом линия уровня уходит в бесконечность, следовательно, на 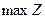 задача не имеет решения вследствие неограниченности целевой функции. Затем перемещаем линию уровня в направлении, противоположном вектору-градиенту до последней точки соприкосновения с ОДР для определения оптимального решения на
задача не имеет решения вследствие неограниченности целевой функции. Затем перемещаем линию уровня в направлении, противоположном вектору-градиенту до последней точки соприкосновения с ОДР для определения оптимального решения на  . Оптимальным решением на
. Оптимальным решением на  является точка В, которая лежит на пересечении прямых
является точка В, которая лежит на пересечении прямых  и
и  . Для определения ее координат необходимо решить систему уравнений:
. Для определения ее координат необходимо решить систему уравнений: 
Откуда  . Таким образом,
. Таким образом,  . Подставив значение
. Подставив значение  и
и  в целевую функцию Z, получаем:
в целевую функцию Z, получаем:
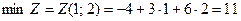 .
.

Рис. 1.3
Ответ:  .
.
Пример 1.8
Графическим методом решить ЗЛП:

Решение
Вначале построим ОДР задачи (рис. 1.4). Для этого в системе координат  на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:


Рис. 1.4
Затем определим, какую полуплоскость определяет соответствующее неравенство, подставив координаты какой-нибудь точки, не лежащей на этой прямой. Ограничение-равенство – это есть сама граничная прямая. Ограничения  означают, что ОДР лежит в I четверти системы координат
означают, что ОДР лежит в I четверти системы координат  . Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и прямой
. Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и прямой  определяет ОДР данной задачи – это отрезок AB.
определяет ОДР данной задачи – это отрезок AB.
Строим вектор-градиент целевой функции  =(–2;–3). Берем произвольную линию уровня целевой функции (на рисунке она обозначена пунктирной линией) и перемещаем ее в направлении вектора-градиента до последней точки соприкосновения с ОДР для определения оптимального решения на
=(–2;–3). Берем произвольную линию уровня целевой функции (на рисунке она обозначена пунктирной линией) и перемещаем ее в направлении вектора-градиента до последней точки соприкосновения с ОДР для определения оптимального решения на 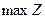 , это есть точка А. Она лежит на пересечении прямых
, это есть точка А. Она лежит на пересечении прямых  и
и  . Для определения ее координат необходимо решить систему уравнений:
. Для определения ее координат необходимо решить систему уравнений: 
Откуда  . Таким образом,
. Таким образом,  . Подставив значение
. Подставив значение  и
и  в целевую функцию Z, получаем:
в целевую функцию Z, получаем:
 .
.
Затем перемещаем линию уровня в направлении, противоположном вектору-градиенту до последней точки соприкосновения с ОДР для определения оптимального решения на  . Оптимальным решением на
. Оптимальным решением на  является точка В, которая лежит на пересечении прямых
является точка В, которая лежит на пересечении прямых  и
и  . Для определения ее координат необходимо решить систему уравнений:
. Для определения ее координат необходимо решить систему уравнений: 
Откуда  . Таким образом,
. Таким образом,  . Подставив значение
. Подставив значение  и
и  в целевую функцию Z, получаем:
в целевую функцию Z, получаем:
 .
.
Ответ:  ,
,  ;
;  ,
,  .
.
Пример 1.9
Графическим методом решить ЗЛП:

Решение
Вначале построим ОДР задачи (рис. 1.5). Для этого в системе координат  на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:

Затем определим, какую полуплоскость определяет соответствующее неравенство, подставив координаты какой-нибудь точки, не лежащей на этой прямой. Ограничения  означают, что ОДР лежит в I четверти системы координат
означают, что ОДР лежит в I четверти системы координат  . Соответствующие полуплоскости на рисунке показаны стрелками. Указанные полуплоскости не имеют ни одной общей точки, следовательно, ОДР – пустое множество и задача не имеет решения вследствие несовместности системы ограничений.
. Соответствующие полуплоскости на рисунке показаны стрелками. Указанные полуплоскости не имеют ни одной общей точки, следовательно, ОДР – пустое множество и задача не имеет решения вследствие несовместности системы ограничений.

Рис. 1.5
Пример 1.10
Графическим методом решить ЗЛП:

Решение
Вначале построим ОДР задачи (рис. 1.6). Для этого в системе координат  на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:

Затем определим, какую полуплоскость определяет соответствующее неравенство, подставив координаты какой-нибудь точки, не лежащей на этой прямой. Ограничения  означают, что ОДР лежит в I четверти системы координат
означают, что ОДР лежит в I четверти системы координат  . Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет ОДР данной задачи – это открытая многоугольная область ABCD.
. Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет ОДР данной задачи – это открытая многоугольная область ABCD.
Строим вектор-градиент целевой функции  =(0;–3). Берем произвольную линию уровня целевой функции (на рисунке она обозначена пунктирной линией) и перемещаем ее в направлении вектора-градиента до последней точки соприкосновения с ОДР для определения оптимального решения на
=(0;–3). Берем произвольную линию уровня целевой функции (на рисунке она обозначена пунктирной линией) и перемещаем ее в направлении вектора-градиента до последней точки соприкосновения с ОДР для определения оптимального решения на 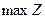 . Такой точкой является любая точка луча CD. Следовательно, на
. Такой точкой является любая точка луча CD. Следовательно, на 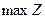 задача имеет бесконечное множество решений – это луч CD. Для нахождения значения целевой функции на этих решениях, найдем координаты любой точки этого луча. Так, например, возьмем С(4;0) и
задача имеет бесконечное множество решений – это луч CD. Для нахождения значения целевой функции на этих решениях, найдем координаты любой точки этого луча. Так, например, возьмем С(4;0) и  .
.
Затем перемещаем линию уровня в направлении, противоположном вектору-градиенту, при этом линия уровня уходит в бесконечность, следовательно, на  задача не имеет решения вследствие неограниченности целевой функции.
задача не имеет решения вследствие неограниченности целевой функции.

Рис. 1.6
Ответ: Оптимальные решения на 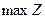 – луч CD,
– луч CD,  .
.
Задачи
Решить ЗЛП графическим методом (1.3.1 – 1.3.12)
1.3.1
а)
 ; ;
 в)
в)
 ; ;
 д)
д)
 ; ;
 ж)
ж)
 ; ;
 и)
и)
 ; ;
 л)
л)
 ; ;
 н)
н)
 ; ;
 1.3.2
а)
1.3.2
а)
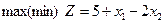 ; ;
 в)
в)
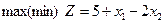 ; ;
 д)
д)
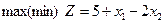
 ж)
ж)
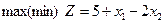
 1.3.3
а)
1.3.3
а)
 ; ;
 в)
в)
 ; ;
 д)
д)
 ; ;
 1.3.4
1.3.4
 ; ;
 1.3.6
1.3.6
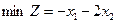 ; ;
 1.3.8
1.3.8
 ; ;
 1.3.10
1.3.10
 ; ;
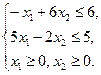 1.3.12
1.3.12
 ; ;

|
б)
 ; ;
 г)
г)
 ; ;
 е)
е)
 ; ;
 з)
з)
 ; ;
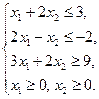 к)
к)
 ; ;
 м)
м)
 ; ;
 о)
о)
 ; ;
 б)
б)
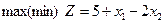 ; ;
 г)
г)
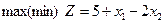 ; ;
 е)
е)
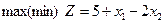
 з)
з)
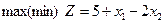
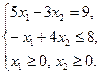 б)
б)
 ; ;
 г)
г)
 ; ;
 е)
е)
 ; ;
 1.3.5
1.3.5
 ; ;
 1.3.7
1.3.7
 ; ;
 1.3.9
1.3.9
 ; ;
 1.3.11
1.3.11
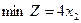 ; ;
 1.3.13
1.3.13
 ; ;

|
1.3.14 – 1.3.16
Решить задачи 1.1.1 – 1.1.3 (соответственно) графическим методом.
1.4. Графический метод решения задач линейного программирования с n переменными
Графическим методом решаются ЗЛП, если в ее канонической форме записи число переменных 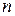 и число линейно независимых уравнений
и число линейно независимых уравнений  связаны соотношением
связаны соотношением  .
.
Алгоритм графического метода решения ЗЛП со многими переменными (n>2)
1) Записать каноническую форму ЗЛП.
2) Выбрать две свободные переменные.
3) Выразить все остальные переменные через свободные, т.е. решить систему ограничений заданной задачи.
4) Выразить целевую функцию через свободные переменные.
5) Полученную двухмерную задачу решить графическим методом.
6) Найдя координаты оптимального решения двухмерной задачи, определяем остальные координаты оптимального решения исходной задачи.
7) Значение целевой функции на оптимальном плане двухмерной задачи совпадает со значением целевой функции на оптимальном плане исходной задачи.
Пример 1.11
Решим графически ЗЛП, математическая модель которой составлена в примере 1.2.
 ;
;

Решение
Перейдем к эквивалентной задаче с двумя переменными.
Математическую модель задачи представим в канонической форме записи:
 ;
;

Пусть переменные  и
и  будут свободными, а все остальные переменные базисными. Выразим все базисные переменные через свободные.
будут свободными, а все остальные переменные базисными. Выразим все базисные переменные через свободные.

Выразим целевую функцию через свободные переменные.

Учитывая условия неотрицательности базовых переменных, получим эквивалентную задачу с двумя переменными:
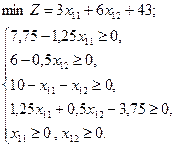 или
или 
Полученную двухмерную задачу решим графическим методом.
Построим ОДР задачи (Рис. 1.7). Для этого в системе координат  на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:

Затем определим, какую полуплоскость определяет соответствующее неравенство, подставив координаты какой-нибудь точки, не лежащей на данной прямой, например (0;0). Ограничения  означают, что ОДР лежит в I четверти системы координат
означают, что ОДР лежит в I четверти системы координат  . Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет ОДР данной задачи – это многоугольник ABCDE.
. Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет ОДР данной задачи – это многоугольник ABCDE.
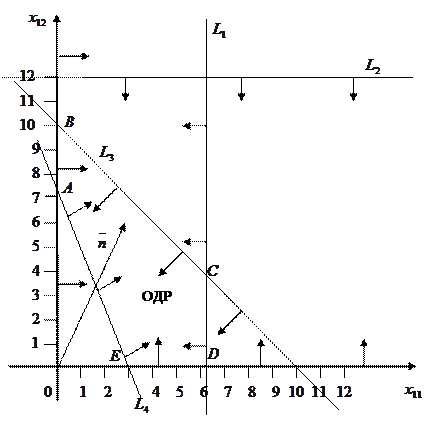
Рис. 1.7
Строим вектор-градиент целевой функции  =(3;6).
=(3;6).
Оптимальное решение достигается в точке E(3;0).

Перейдем к решению исходной задачи. Т.е. найдем значения базисных переменных:

Итак, решение исходной задачи:  ,
,  .
.
Экономический смысл полученного решения задачи:
для того, чтобы затраты были минимальными и составили 52 усл. ден. ед. необходимо, чтобы оборудование А1 выпускало 3 часа продукцию P1, оборудование А2 выпускало 4 часа продукцию P1 и 6 часов продукцию P2.
Преобразовать ЗЛП к эквивалентной двумерной ЗЛП можно и не записывая исходную задачу в канонической форме. Достаточно из ограничений-равенств системы выразить базисные переменные через выбранные две свободные и подставить это выражение всюду, где они встречаются в ограничениях-неравенствах и в целевой функции. Учитывая условия неотрицательности базисных переменных двумерная модель будет иметь то же количество ограничений, что и исходная. Таким образом, графическим методом можно решить лишь ту ЗЛП с n переменными, система ограничений которой имеет не менее n –2 линейно-независимых ограничений-равенств.
Пример 1.12
Решим графически ЗЛП:
 ;
;

Решение
Перейдем к эквивалентной задаче с двумя переменными.
Пусть переменные  и
и 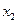 будут свободными, а все остальные переменные базисными. Выразим все базисные переменные через свободные. Сделаем это последовательно. Сначала выразим, например, из второго ограничения-равенства базисную переменную
будут свободными, а все остальные переменные базисными. Выразим все базисные переменные через свободные. Сделаем это последовательно. Сначала выразим, например, из второго ограничения-равенства базисную переменную  и подставим это выражение всюду, где она встречается в модели:
и подставим это выражение всюду, где она встречается в модели:
 ;
;

Раскрыв скобки, приведя подобные и учитывая условие неотрицательности переменной  , получим следующую модель от трех переменных, эквивалентную исходной:
, получим следующую модель от трех переменных, эквивалентную исходной:
 ;
;

Затем выразим, например, из первого ограничения-равенства базисную переменную  и подставим это выражение всюду, где она встречается в модели:
и подставим это выражение всюду, где она встречается в модели:
 ;
;
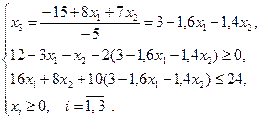
Раскрыв скобки, приведя подобные и учитывая условие неотрицательности переменной  , получим следующую модель от двух переменных, эквивалентную исходной:
, получим следующую модель от двух переменных, эквивалентную исходной:
 или
или 
Полученную двухмерную задачу решим графическим методом.
Построим ОДР задачи (Рис. 1.8). Для этого в системе координат  на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:

Затем определим, какую полуплоскость определяет соответствующее неравенство, подставив координаты какой-нибудь точки, не лежащей на данной прямой, например (0;0). Ограничения  означают, что ОДР лежит в I четверти системы координат
означают, что ОДР лежит в I четверти системы координат  . Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет ОДР данной задачи – это треугольник ABC.
. Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет ОДР данной задачи – это треугольник ABC.
Вектор-градиент целевой функции  =(7,8;12,2). Так как нас интересует направление вектора-градиента, а не его длина, то можно изобразить вектор
=(7,8;12,2). Так как нас интересует направление вектора-градиента, а не его длина, то можно изобразить вектор  =(3,9;6,1)=0,5
=(3,9;6,1)=0,5  , который в два раза меньше вектора градиента.
, который в два раза меньше вектора градиента.

Рис. 1.8
Оптимальное решение достигается в точке В, которая лежит на пересечении прямой  и оси
и оси  . Для определения ее координат необходимо решить систему уравнений:
. Для определения ее координат необходимо решить систему уравнений: 
Откуда 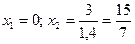 . Таким образом,
. Таким образом,  . Подставив значение
. Подставив значение  и
и  в целевую функцию Z, получаем:
в целевую функцию Z, получаем:
 .
.
Перейдем к решению исходной задачи. Т.е. найдем значения базисных переменных:
 ,
,
 .
.
Итак, решение исходной задачи:  ,
, 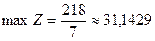 .
.
Задачи
Решить ЗЛП графическим методом (1.4.1 – 1.4.8)
1.4.1
 ; ;
 1.4.3
1.4.3
 ; ;
 1.4.5
1.4.5
 ; ;
 1.4.7
1.4.7
 ; ;

| 1.4.2
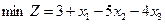 ; ;
 1.4.4
1.4.4
 ; ;
 1.4.6
1.4.6
 ; ;
 1.4.8
1.4.8
 ; ;

|
1.4.9 – 1.4.11
Решить задачи 1.1.4, 1.1.9, 1.1.11 (соответственно) графическим методом.
1.5. Симплексный метод решения задач линейного программирования
Симплексный метод основывается на следующем:
· ОДР ЗЛП является выпуклым множеством с конечным числом угловых точек, т.е. многогранником или многоугольным множеством;
· оптимальным решением ЗЛП является одна из угловых точек ОДР, если оптимальное решение единственно и не более двух угловых точек ОДР, если оптимальных решений бесконечное множество;
· угловые точки ОДР алгебраически представляют некоторые опорные решения системы ограничений задачи (опорные планы).
Данный метод состоит в целенаправленном переборе опорных решений ЗЛП. Он позволяет за конечное число шагов расчета либо найти оптимальное решение, либо установить его отсутствие.
Алгоритм решения ЗЛП симплексным методом
1) Привести ЗЛП к каноническому виду с неотрицательной правой частью.
2) Найти какой-либо начальный опорный план  . Если опорный план отсутствует, то задача не имеет решения вследствие несовместности системы ограничений.
. Если опорный план отсутствует, то задача не имеет решения вследствие несовместности системы ограничений.
3) Проверить найденный план на оптимальность, используя оценки заполненной симплексной таблицы.
4) Если план оптимален, то задача решена.
5) Если план оптимален, но не единственен, то можно найти еще один оптимальный план.
6) Если план не оптимален, но имеет место условие неограниченности целевой функции, то задача не имеет решения.
7) Если пункты 4) – 6) алгоритма не выполняются, найти новый опорный план и перейти к пункту 3).
Нахождение начального опорного плана ЗЛП (  )
)
Пусть система ограничений ЗЛП представлена в канонической форме записи с неотрицательной правой частью.

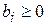
 .
.
Говорят, что ограничение ЗЛП имеет предпочтительный вид, если при неотрицательной правой части (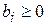 ) левая часть ограничения содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения-равенства – с коэффициентом, равным нулю.
) левая часть ограничения содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения-равенства – с коэффициентом, равным нулю.
Например, в системе ограничений:

первое и второе ограничения имеют предпочтительный вид, а третье – нет (предпочтительные переменные подчеркнуты).
Если каждое ограничение системы имеет предпочтительный вид, то система представлена в предпочтительном виде. В этом случае легко найти ее опорное решение. Предпочтительные переменные будут базисными, а остальные – свободными. Все свободные переменные нужно приравнять к нулю, тогда базисные переменные будут равны свободным членам.
Например, в системе ограничений:

предпочтительными (базисными) являются переменные  , свободными являются переменные
, свободными являются переменные  .
.
Приравниваем свободные переменные  к нулю, тогда базисные переменные примут значения:
к нулю, тогда базисные переменные примут значения:  ,
, 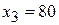 ,
,  .
.
Получим начальный опорный план  .
.
В случае, когда в каноническом виде с неотрицательной правой частью система ограничений ЗЛП не имеет предпочтительного вида, то начальный опорный план можно найти методом искусственного базиса или методом Жордановых исключений.
Нахождение начального опорного плана ЗЛП методом искусственного базиса
В случае, когда ограничение-равенство системы не имеет предпочтительного вида, к его левой части добавляют искусственную переменную 
 . В целевую функцию переменные
. В целевую функцию переменные 
 вводят с коэффициентом «M» в случае решения задачи на минимум и с коэффициентом «–М» в случае решения задачи на максимум, где М – большое (по сравнению с остальными коэффициентами целевой функции) положительное число. Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид.
вводят с коэффициентом «M» в случае решения задачи на минимум и с коэффициентом «–М» в случае решения задачи на максимум, где М – большое (по сравнению с остальными коэффициентами целевой функции) положительное число. Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид.
Пусть ЗЛП имеет каноническую форму записи с неотрицательной правой частью:

где 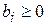
 .
.
Если ни одно из ограничений не имеет предпочтительной переменной, то М-задача запишется так:

Тогда начальный опорный план этой задачи: 
Если некоторое уравнение системы имеет предпочтительный вид, то в него не следует вводить искусственную переменную.
Пример 1.13
Найти начальный опорный план ЗЛП методом искусственного базиса и значение целевой функции на этом плане:
 ;
;

Решение
Запишем ЗЛП в каноническом виде с неотрицательной правой частью.
 ;
;

Составим М-задачу:
 ;
;

Тогда начальный опорный план:  , значение целевой функции на этом плане:
, значение целевой функции на этом плане:  .
.
Пример 1.14
Найти начальный опорный план ЗЛП методом искусственного базиса и значение целевой функции на этом плане:
 ;
;

Решение
Запишем ЗЛП в каноническом виде с неотрицательной правой частью.
 ;
;

Составим М-задачу:
 ;
;

Тогда начальный опорный план:  , значение целевой функции на этом плане:
, значение целевой функции на этом плане:  .
.
Пример 1.15
Найти начальный опорный план ЗЛП методом искусственного базиса и значение целевой функции на этом плане:
 ;
;

Решение
Запишем ЗЛП в каноническом виде с неотрицательной правой частью.
 ;
;

где  .
.
Составим М-задачу:
 ;
;

где  .
.
Тогда начальный опорный план:  , значение целевой функции на этом плане:
, значение целевой функции на этом плане: 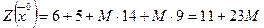 .
.
Нахождение начального опорного плана ЗЛП методом Жордановых исключений
В случае, когда ограничение-равенство системы не имеет предпочтительного вида, его необходимо записать как 0-равенство, т.е. левую часть ограничения переносят в скобках со знаком минус в правую часть, при этом в левой части остается ноль. Если ограничение-равенство системы имеет предпочтительный вид, то предпочтительную (базисную) переменную оставляют в левой части ограничения, а все остальное из левой части переносят в скобках со знаком минус в правую часть. Переменные, которые оказались при этом в правых частях ограничений, являются свободными. Целевая функция должна быть выражена только через свободные переменные и записана в идентичном виде, т.е. от свободного члена отнимают скобку с остальными элементами целевой функции (при этом целевая функция не должна измениться).
Пусть ЗЛП имеет каноническую форму записи с неотрицательной правой частью:

где 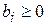
 .
.
Если ни одно из ограничений не имеет предпочтительной переменной, то задача будет записана следующим образом:


где 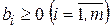 .
.
Для нахождения начального опорного плана методом Жордановых исключений необходимо исходя из вида задачи (1.18 – 1.19) заполнить таблицу Жордана и преобразовывать ее до тех пор (см. шаг Жордановых исключений), пока не будет найден начальный опорный план или пока не убедимся, что опорный план отсутствует и задача не имеет решения вследствие несовместности системы ограничений.
Таблица Жордана содержит  столбцов, где
столбцов, где 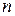 – число переменных,
– число переменных,  – число предпочтительных (базисных) переменных и
– число предпочтительных (базисных) переменных и 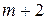 строки, где
строки, где  – число ограничений-равенств. В первом столбце «БП» записываются базисные (предпочтительные) переменные. Если ограничение не имеет предпочтительной переменной, то записывается «0». Второй столбец «1» – столбец свободных членов
– число ограничений-равенств. В первом столбце «БП» записываются базисные (предпочтительные) переменные. Если ограничение не имеет предпочтительной переменной, то записывается «0». Второй столбец «1» – столбец свободных членов 
 системы ограничений (1.19) а в
системы ограничений (1.19) а в 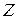 -строке – элемент
-строке – элемент  из (1.18). Остальные столбцы таблицы – «СП», в основной части которых находятся элементы
из (1.18). Остальные столбцы таблицы – «СП», в основной части которых находятся элементы  из системы (1.19). В
из системы (1.19). В 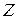 -строке в столбцах «СП» записываются коэффициенты при свободных переменных, стоящие в скобках выражения (1.18). Каждому ограничению-равенству из системы (1.19) соответствует строка основной части таблицы. Целевой функции (1.18) соответствует последняя строка таблицы.
-строке в столбцах «СП» записываются коэффициенты при свободных переменных, стоящие в скобках выражения (1.18). Каждому ограничению-равенству из системы (1.19) соответствует строка основной части таблицы. Целевой функции (1.18) соответствует последняя строка таблицы.
Исходя из вида задачи (1.18 – 1.19) за