Закрытая и открытая модели транспортной задачи

Модель ТЗ называют закрытой (сбалансированной), если суммарный объем груза всех поставщиков, равен суммарному спросу потребителей, т.е. выполняется равенство:

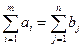. (2.3)

Если для транспортной задачи выполняется одно из условий:

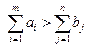, (2.4)

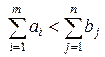, (2.5)

то модель задачи называют открытой (несбалансированной).

Для составления математической модели и для решения ТЗ с открытой моделью необходимо преобразовать ее в закрытую модель.

Так, при выполнении условия (2.4) необходимо ввести фиктивного (n+ 1)-ого потребителя 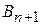, то есть в матрице задачи добавляется столбец. Спрос фиктивного потребителя полагают равным небалансу, то есть 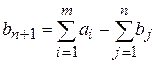, а тарифы равными нулю, то есть 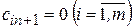. Переменные – это объем груза, который останется у i -ого поставщика.

Аналогично, при выполнении условия (2.5) вводится фиктивный поставщик 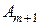, то есть в матрице задачи добавляется строка. Запас груза фиктивного поставщика равен: 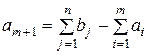, а тарифы равными нулю, то есть 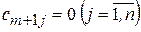. Переменные 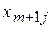– это объем груза, на который запрос j -ого потребителя останется неудовлетворенным.

При преобразовании открытой модели задачи в закрытую модель, целевая функция не изменяется, так как все слагаемые, соответствующие дополнительным перевозкам, равны нулю.

Целевая функция (2.1) и система ограничений (2.2) являются математической моделью сбалансированной ТЗ.

Пример 2.1

В трех хранилищах 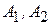и 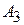имеется соответственно 70, 90 и 50 т топлива. Требуется спланировать перевозку топлива четырем потребителям 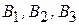и 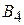, спрос которых равен соответственно 50, 70, 40 и 40т так, чтобы затраты на транспортировку были минимальными. Стоимость перевозки 1т (в усл. ден. ед.) указана в табл. 2.2.

Таблица 2.2

	Потребители	Запас топлива, т
Хранилища
Потребность в топливе, т

Составить математическую модель транспортной задачи.

Решение

Т.к. условие (2.3) не выполнено, то задача несбалансированная. Приведем ее к сбалансированному виду. Поскольку запасы топлива в хранилищах (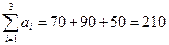) превышают спрос потребителей (), введем фиктивного потребителя , спрос которого равен 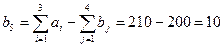. Все тарифы фиктивного потребителя будут равны нулю, т.е. 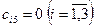. Распределительная таблица примет вид:

Таблица 2.3

	Потребители	Запас топлива, т
Хранилища
Потребность в топливе, т

Составим математическую модель сбалансированной транспортной задачи.

Обозначим 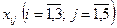– объемы перевозок топлива от -го хранилища -му потребителю.

;

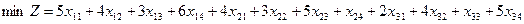2.2. Решение транспортной задачи

Опорным планом ТЗ называется любой допустимый план, в котором число отличных от нуля переменных 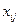будет не больше 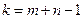. Опорный план будет невырожденным, если число базисных (отличных от нуля) переменных 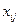будет равно .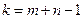