Практическое занятие №4
Тема: Решение задач на расчет энтальпий, энтропий, энергия Гиббса химических реакций Цель: провести практические расчеты законов термодинамики к химическим системам. Определить тепловые эффекты химических реакций, а также определить возможность самопроизвольного протекания этих реакций.
Теоретические основы
Термодинамика – наука, которая изучает общие законы взаимного превращения энергии из одной формы в другую.
Химическая термодинамика решает два основных вопроса:
– количественное определение тепловых эффектов различных процессов;
– выяснение принципиальной возможности самопроизвольного течения химических реакций и условия, при которых химические реакции могут находиться в состоянии равновесия.
Объектом исследования термодинамики является термодинамическая система.
Термодинамическая система – это такая система, в которой между телами, ее составляющими, возможен обмен энергией и веществом, которая полностью описывается термодинамическими параметрами.
Параметры состояния: масса, концентрация, состав, температура, давление, объем и др. Среди них выделяют три основных параметра состояния: давление, температура, объем. Названы они таким образом потому, что незначительные изменения одного или нескольких основных параметров состояния приводят к очень резким изменениям в свойствах термодинамических систем.
Все процессы, протекающие в живых организмах, являются изобарно-изотермическими (P = const; T = const).
Параметры состояния, не поддающиеся непосредственному измерению и зависящие от основных параметров состояния, называются функциями основных параметров состояния. К ним относятся:
|
|
– внутренняя энергия (U) – это полная энергия системы, включающая энергию движения атомов и молекул, электронов и ядер в атомах, внутриядерную энергию, энергию межмолекулярного взаимодействия и другие виды энергий, за исключением кинетической и потенциальной энергии системы как целого:
;
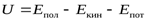– энтальпия (H) – характеризует энергетическое состояние системы при изобарно-изотермических условиях;
– энтропия (S) – мера вероятности состояния термодинамической системы;
– свободная энергия Гиббса или изобарно-изотермический потенциал (G).
Значения этих функций связаны с особенностями состава, внутреннего строения вещества, а также внешними условиями протекания процесса: давлением, температурой, концентрацией вещества.
Абсолютные величины этих функций определить невозможно, можно найти изменение этих величин при переходе термодинамической системы из начального в конечное состояние (из исходных веществ в продукты реакции):
∆ 
,
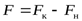где F – функция состояния (U, H, S, G).
Ответить на первый вопрос термодинамики – следовательно, определить величину изменения энтальпии или тепловой эффект химической реакции (ΔН0 х.р., кДж). Этим вопросом занимается раздел термодинамики, называемый термохимией.
Термохимические расчёты основаны на следствии из закона Гесса: изменение энтальпии химической реакции равно сумме энтальпий образования продуктов реакции за вычетом сумм энтальпий образования исходных веществ с учётом стехиометрических коэффициентов.
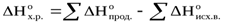
Например, для реакции:
CH4(г) + 2O2(г) = 2H2O(ж) + CO2(г);
Энтальпией образования сложного соединения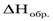 
называется изменение энтальпии в процессе получения одного моля этого соединения из простых веществ, находящихся в устойчивом агрегатном состоянии при данных условиях.
|
|
Обычно энтальпию образования различных соединений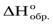 
определяют в стандартных условиях:
t o = 25 oC (298 K);
P = 1атм (760 мм рт.ст.; 101325 Па);
C вещ. = 1 моль/л.
Например, для процесса:
Ca(т) + 0,5O2(г) = CaO(т); ∆HCaO(т) = – 635 кДж/моль
стандартные энтальпии образования всех простых веществ принимают равными нулю:.
Если тепловой эффект имеет отрицательное значение (< 0), такой процесс протекает с выделением энергии и называется экзотермическим, если тепловой эффект имеет положительное значение (>0), то такой процесс протекает с поглощением энергии и называется эндотермическим.
В термохимии принято записывать процессы в виде термохимических уравнений, в которых указывается тепловой эффект или количество теплоты (Q), агрегатное состояние веществ и допускаются дробные коэффициенты:
H2(г) + 0,5O2(г) = H2О(ж); = – 285,8 кДж/моль или
H2(г) + 0,5O2(г) = H2О(ж) + 285,8 кДж/моль, т.к. = – Q.
Ответить на второй вопрос термодинамики – следовательно, определить возможность самопроизвольного течения процесса.
Самопроизвольным называется такой процесс, который протекает без сообщения ему дополнительной энергии. Например, самопроизвольными являются процессы коррозии металлов, окисления жиров, старения резины и многих полимерных материалов, получение растворов и т.д.
Большинство химических процессов протекают самопроизвольно в сторону уменьшения запаса внутренней энергии или энтальпии системы. Но известны и такие процессы, которые протекают самопроизвольно, без изменения внутренней энергии системы, движущей силой таких процессов является энтропия S системы. Энтропия характеризует беспорядок в системе: чем выше беспорядок, тем выше энтропия. В изолированных от внешней среды системах процессы протекают самопроизвольно в направлении увеличения энтропии (∆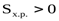 
).
|
|
Энтропия реакции рассчитывается по следствию из закона Гесса и имеет единицу измерения Дж/моль·K.
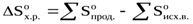
Таким образом, существуют два основных фактора самопроизвольного протекания процессов:
– уменьшение внутренней энергии или энтальпии системы (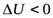
; ∆ 
);
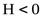– увеличение беспорядка или энтропии системы (∆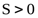 
).
В термодинамике существует параметр, который отражает влияние на направление процесса двух рассмотренных факторов одновременно. Таким параметром для процессов, протекающих при постоянной температуре и давлении, является изобарно-изотермический потенциал ∆ G (или энергия Гиббса, свободная энергия системы). Изменение изобарно-изотермического потенциала химической реакции можно рассчитать по формуле Гиббса:
∆ G T,х.р. = ∆Hoх.р. – T ∆Soх.р.,
где T – абсолютная температура процесса, K;
∆ G х.р. характеризует общую движущую силу процесса, кДж.
Если процесс протекает в стандартных условиях, то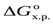 
рассчитывается по следствию из закона Гесса.
.
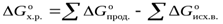Если процесс является обратимым, для которого известна величина константы равновесия (K р), то можно воспользоваться формулой:
,
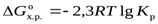где R – универсальная газовая постоянная (R = 8,3144 Дж/моль·K);
Т – абсолютная температура процесса, K;
K р – константа равновесия процесса.
Величина и знак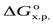 
характеризует принципиальную возможность протекания процесса:
– если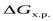 
< 0, процесс протекает самопроизвольно при данных условиях;
– если 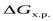> 0, процесс при данных условиях протекать не может;
Примеры решения задач.
Задача 1. Определите по справочным данным стандартную энтальпию реакции
С2H5OH(ж) + 3O2(г) = 2СО2(г) + 3H2O(г).
Решение:
Значение энтальпии реакции находим по первому следствию закона Гесса:
ΔHр-ции = ΣH0кон – ΣH0исх кДж/моль
Подставив стандартные величины, получим:
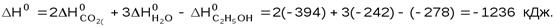
Ответ: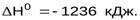 
Задача 2. Рассчитайте стандартную энтальпию и стандартную энтропию химической реакции. Определите в каком направлении при 298 °К (прямом или обратном) будет протекать реакция. Рассчитайте температуру, при которой равновероятны оба направления реакции.
Fe2O3 (к) + 3H2 = 2Fe(к) + 3H2O(г)
Решение.
ΔHр-ции = ΣH0кон – ΣH0исх кДж/моль
Запишем термохимическое уравнение для данной реакции с учетом стехиометрических коэффициентов:
ΔHр-ции = 2· ΔH0 Fe + 3· ΔH0 H2O - ΔH0 Fe2O3 - 3· ΔH0 H2
Используя справочные данные стандартных энтальпий веществ подставляем в уравнение и находим:
ΔHр-ции = 2·0 + 3·(- 241,82) – (-822,16) - 3·0 = 96,7 кДж/моль
Энтропия реакции рассчитывается по следствию из закона Гесса:
ΔSр-ции=ΣS0кон – ΣS0исх Дж/(моль·K)
Запишем термохимическое уравнение для данной реакции с учетом стехиометрических коэффициентов:
ΔSр-ции = 2· ΔS0 Fe + 3· ΔS0 H2O - ΔS0 Fe2O3 - 3· ΔS0 H2
Используя справочные данные стандартных энтропий веществ, находим:
ΔSр-ции = 2·27,15 + 3·188,7 – 89,96 — 3·131 = 137,44 Дж/(моль·K)
Изменение изобарно-изотермического потенциала химической реакции можно рассчитать по формуле Гиббса:
ΔG = ΔH – TΔS
Подставим полученные значения в это уравнение:
ΔG = 96,7 – 298 ·137,44 /1000 = 55,75 кДж/моль
При Т=298°К, ΔG > 0 – реакция не идет самопроизвольно, т.е. реакция будет протекать в обратном направлении.
Чтобы рассчитать температуру, при которой равновероятны оба направления реакции, надо ΔG приравнять к нулю:
ΔG = ΔH – TΔS = 0,
Тогда:
T= - (ΔG – ΔH) / ΔS= - (0-96,7)/0,137 = 705,83 K
При Т = 705,83 К реакция будет идти равновероятно как в прямом, так и в обратном направлении.
Ответ: ΔHр-ции = 96,7 кДж/моль; ΔSр-ции = 137,44 Дж/(моль·K); ΔG = 55,75 кДж/моль; T= 705,83K
Задача 3. Вычислите энергию Гиббса и определите возможность протекания реакции при температурах 1000 и 3000 К.
Cr2O3 (т) + 3C (т) = 2Cr (т) + 3CO (г)
Cr2O3 (т)
C (т)
Cr (т)
CO (г)
ΔH298, кДж/моль
- 1141
- 110,6
ΔS298, Дж/(моль×К)
81,2
5,7
23,6
197,7
Решение.
Вычисления энергии Гиббса проводим согласно выражению:
ΔGр-ции = ΔHр-ции – TΔSр-ции
Необходимо рассчитать энтальпию и энтропию химической реакции.
ΔHр-ции = ΣH0кон – ΣH0исх кДж/моль
Используя справочные данные стандартных энтальпий веществ, находим:
ΔHр-ции= 2· ΔH0 Cr + 3· ΔH0 CO — ΔH0 Cr2O3 — 3· ΔH0 C= 2·0 + 3·(- 110,6) – (-1141) — 3·0 = 809,2 кДж/моль
ΔSр-ции=ΣS0кон – ΣS0исх Дж/моль·K
Аналогично, используя справочные данные стандартных энтропий веществ, находим:
ΔSр-ции= 2· ΔS0 Cr + 3· ΔS0 CO — ΔS0 Cr2O3 — 3· ΔS0 C= 2·23,6 + 3·197,7 – 81,2 — 3·5,7 = 542 Дж/(моль·K)
Найдем энергию Гиббса при 1000 К
ΔG1000 = ΔH – TΔS = 809,2 – 1000 ·542 /1000 = 267,2 кДж/моль
ΔG1000 > 0, следовательно, реакция самопроизвольно не идет.
Найдем энергию Гиббса при 3000 К
ΔG3000= ΔH – TΔS = 809,2 – 3000 ·542 /1000 = — 816,8 кДж/моль
ΔG3000 ˂ 0, следовательно, реакция протекает самопроизвольно.
Ответ: ΔG1000 = 267,2 кДж/моль - реакция самопроизвольно не идет.
ΔG3000 = - 816,8 кДж/моль - реакция протекает самопроизвольно
Выполнение работы
Решите следующие задачи
1) Вычислите стандартную энтальпию реакции. Справочные даны смотрите в приложении 1.
2) Рассчитайте стандартную энтальпию и стандартную энтропию химической реакции. Определите в каком направлении при 298 °К (прямом или обратном) будет протекать реакция. Рассчитайте температуру, при которой равновероятны оба направления реакции. Справочные данные смотрите в приложении 1.
1) NH3 (г) + 5O2 (г) = 4NO(г) + 6Н2О(г)
2) 4НС1(г) + О2 (г) = 2Н2О(г) + 2Cl2 (г)
3) CaCO3 (т) = CaO(m) + CO2 (г)
4) Fe3O4 (т) + H2 (г) = 3FeO(m) + Н2O(г)
5) Ca(OH)2 (т) + CO2 (г) = CaCa 3 (т) + Н2О(г)
3) Вычислите энергию Гиббса и определите возможность протекания реакции при температурах 600 и 3450 К. Справочные данные смотрите в приложении 1.
1) FeS2 (т) + 11О2 (г) = 2Fe2O3 (т) + 8SO2 (г)
2) Zn(к) + ½О2(г) = ZnO(к)
3) 3Cu(тв) + 8HNO3(ж) = 3Cu(NO3)2(тв) + 2NO(г) + 4H2O(ж)
4) 2H2O(г.) + CH4(г.) = CO2(г.) + 4H2(г.).
5) CH4(г) + СО2(г) = 2CO(г) + 2Н2(г)
Контрольные вопросы:
1.Сформулируйте второй закон термодинамики.
2. Какие системы называются термодинамическими?
3. Дайте определение теплового эффекта реакции
4. Сформулируйте закон Гесса.
5. Какие процессы называются экзо- и эндо-термическими?
6. Какие процессы называются самопроизвольными
Сформулируйте вывод по работе
Оценка выполненной работы: 3 балла
| Критерий оценки | Балл |
| Работа не выполнена | |
| Работа выполнена не в полном объеме | |
| Работа выполнена в полном объеме, без ошибок |
ПРИЛОЖЕНИЕ