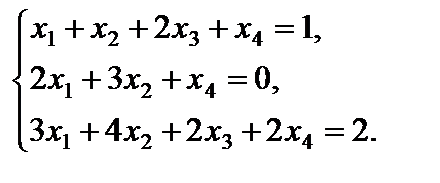Задачи для самостоятельной работы
1. Даны матрицы
Найти матрицы: A + B, 2 A, A – 3 B, AT, BT, ABT.
2. Даны матрицы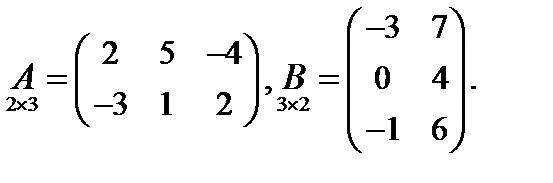 
Найти произведения AB и BA.
Решение системы линейных алгебраических уравнений
По формулам Крамера
Пример 11. Решить систему:
.
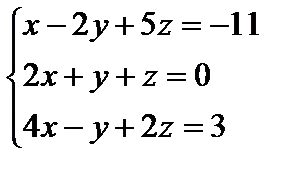Решение.
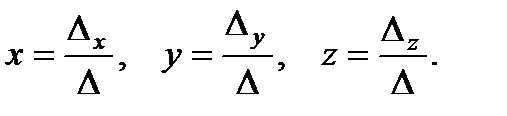
1) Находим определитель системы.
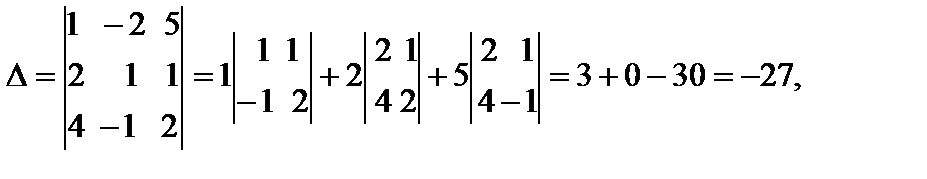
т. к.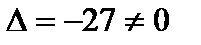 
, то решение системы существует и единственно.
2) Находим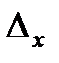 
. Для этого 1-ый столбец в определителе системы заменяем столбцом свободных членов.
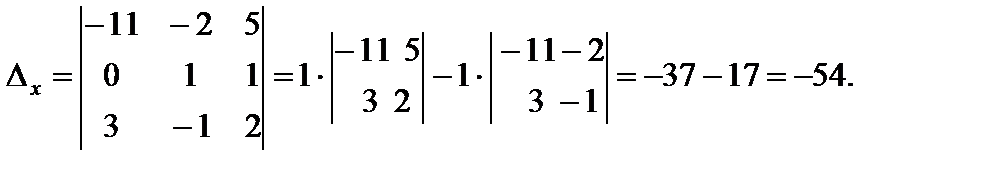
Находим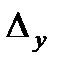 
. Для этого 2-ой столбец в определителе системы заменяем столбцом свободных членов.
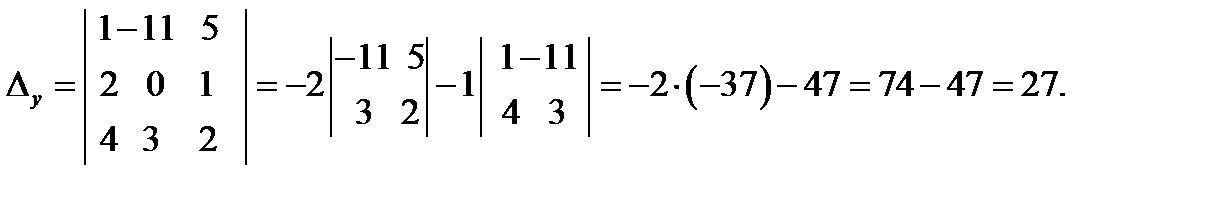
Находим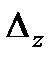 
. Для этого 3-ий столбец в определителе системы заменяем столбцом свободных членов.
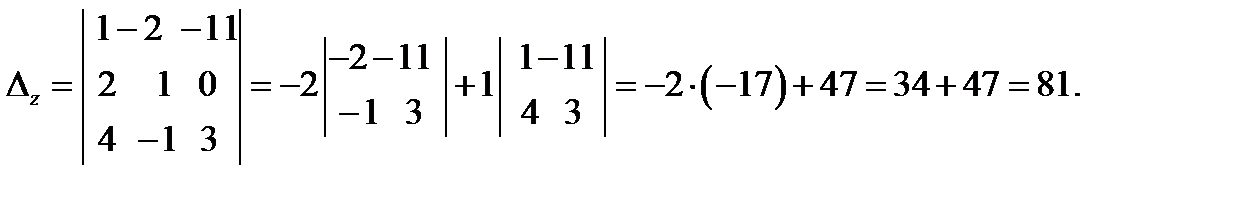
3) Находим неизвестные x, y, z:
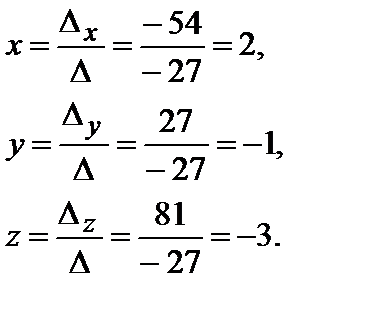
Ответ: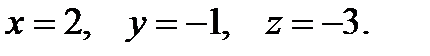 
Обратная матрица
Рассмотрим квадратную матрицу A порядка n:
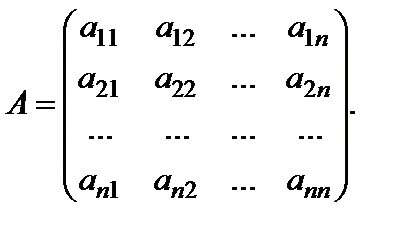
Квадратная матрица называется невырожденной, если её определитель не равен нулю.
Матрица A –1 называется обратной квадратной матрице A, если
A · A –1 = A –1· A = E..
Пример 12. Дана матрица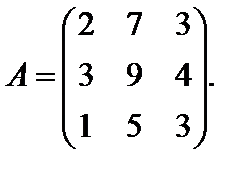 
Найти обратную.
Решение. Находим определитель матрицы:
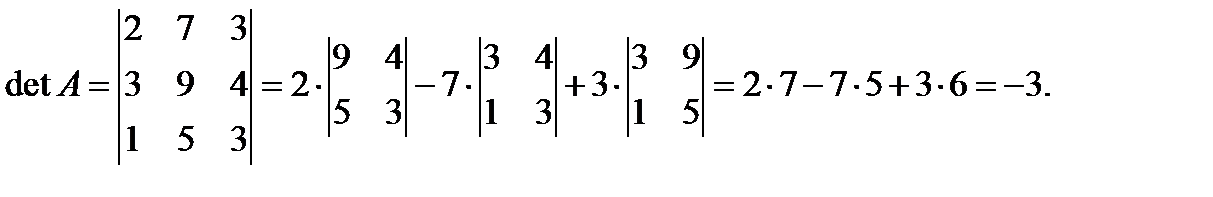
Находим алгебраические дополнения элементов данной матрицы:
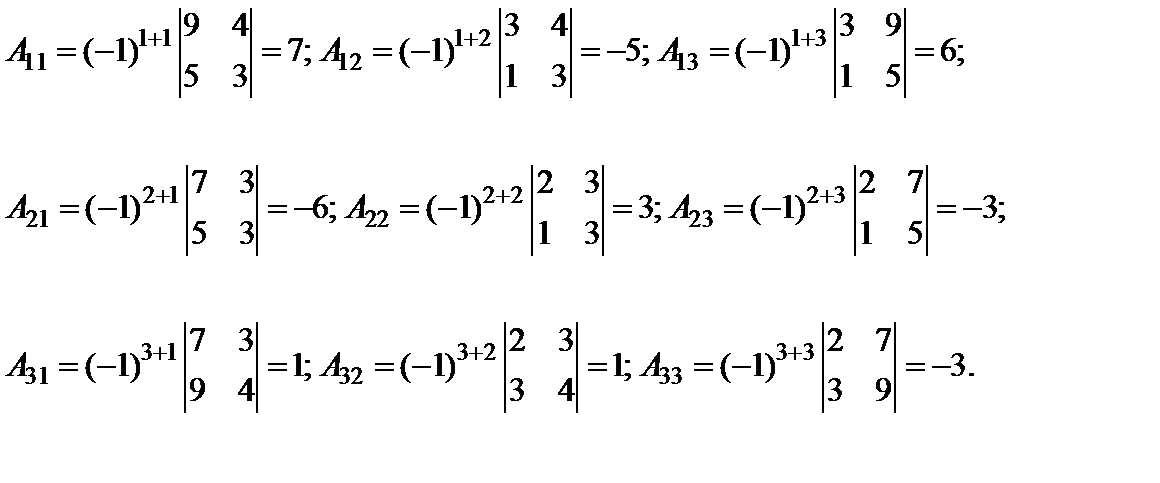
Составим матрицу алгебраических дополнений (Aij) и, транспонировав ее, найдем присоединенную матрицу Ã:
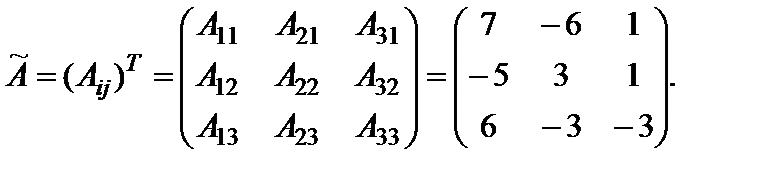
Разделив все элементы присоединенной матрицы Ã на определитель матрицы A, находим обратную матрицу A –1:
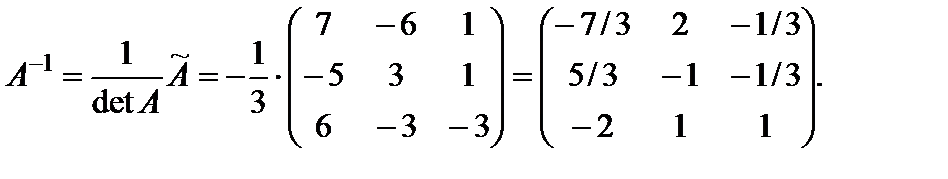
Теорема. Рассмотрим квадратную систему линейных уравнений, записанную в матричном виде: AX = B. Пусть матрица A системы невырожденная, т.е. det A ≠ 0. Тогда система линейных уравнений имеет единственное решение:
| X = A –1 B |
Пример 13. Решить систему линейных уравнений:
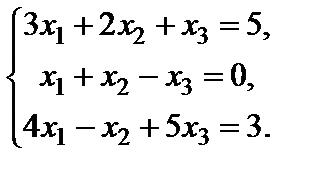
Решение. Метод обратной матрицы.
Введем матрицы: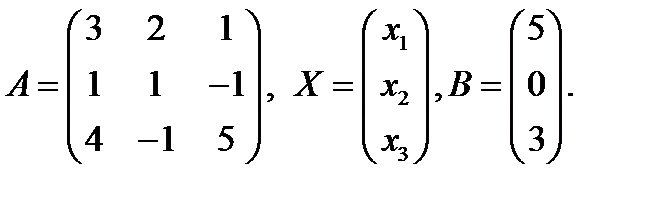 
Вычислим определитель матрицы системы
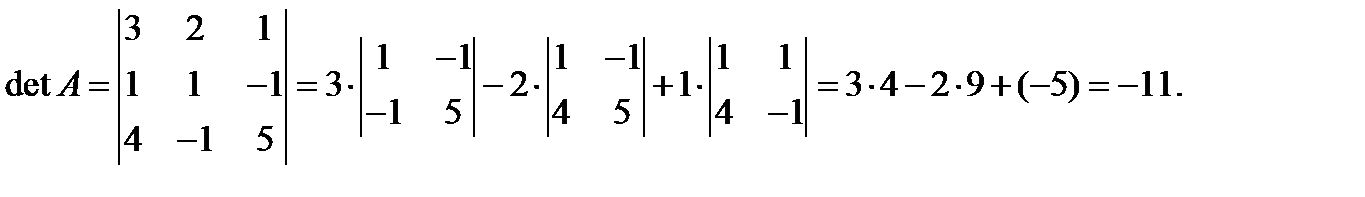
Так как det A ≠ 0, то существует обратная матрица, и решение может быть найдено по формуле X = A –1 B.
Найдем алгебраические дополнения элементов матрицы A:
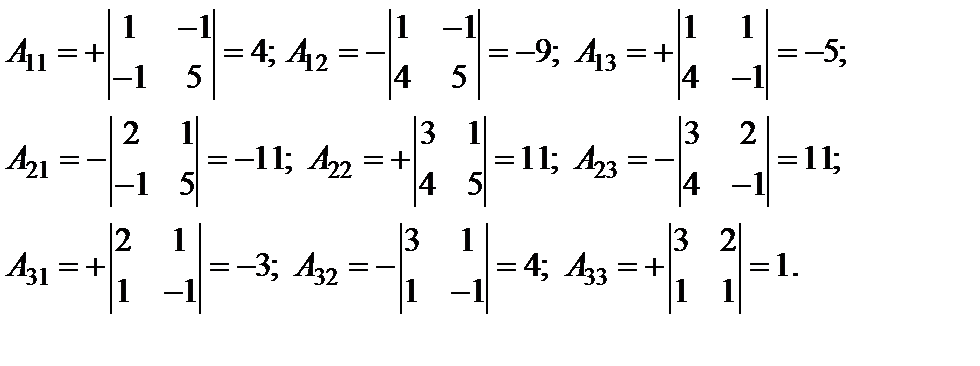
Найдем обратную матрицу по формуле:
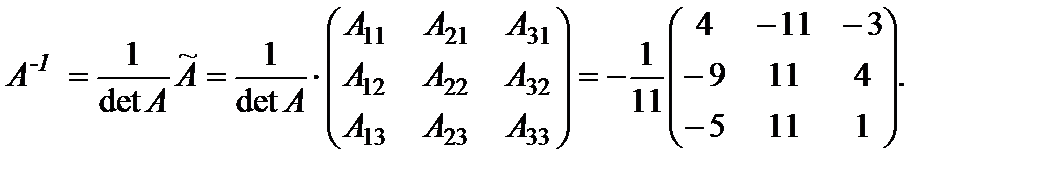
Применяя формулу (4) теоремы 2.1, получим решение системы:
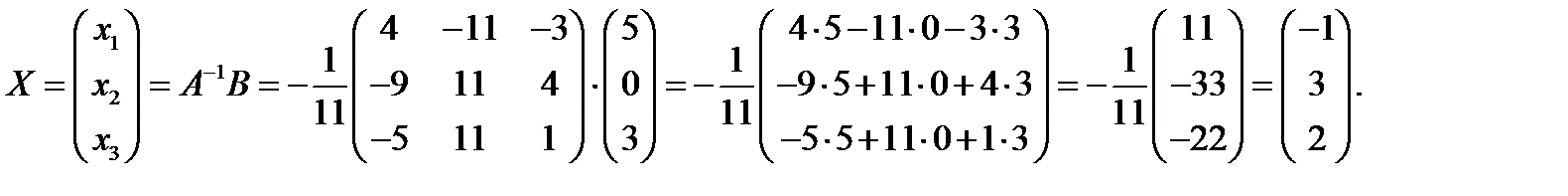
Таким образом, x 1 = –1, x 2 = 3, x 3 = 2.
Пример 14. Решить систему: 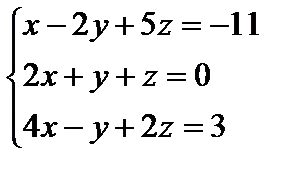методом обратной матрицы.
Решение. Определитель системы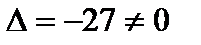 
, следовательно, обратная матрица существует. Матрицу неизвестных 
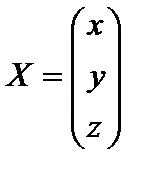найдём из уравнения:
.
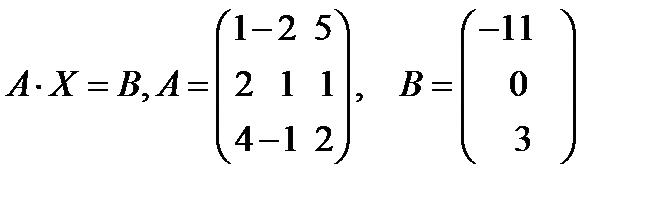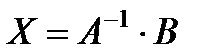
1) Находим транспонированную матрицу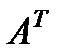 
.
.
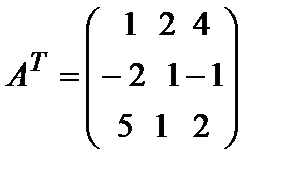2) Находим присоединённую матрицу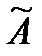 
.
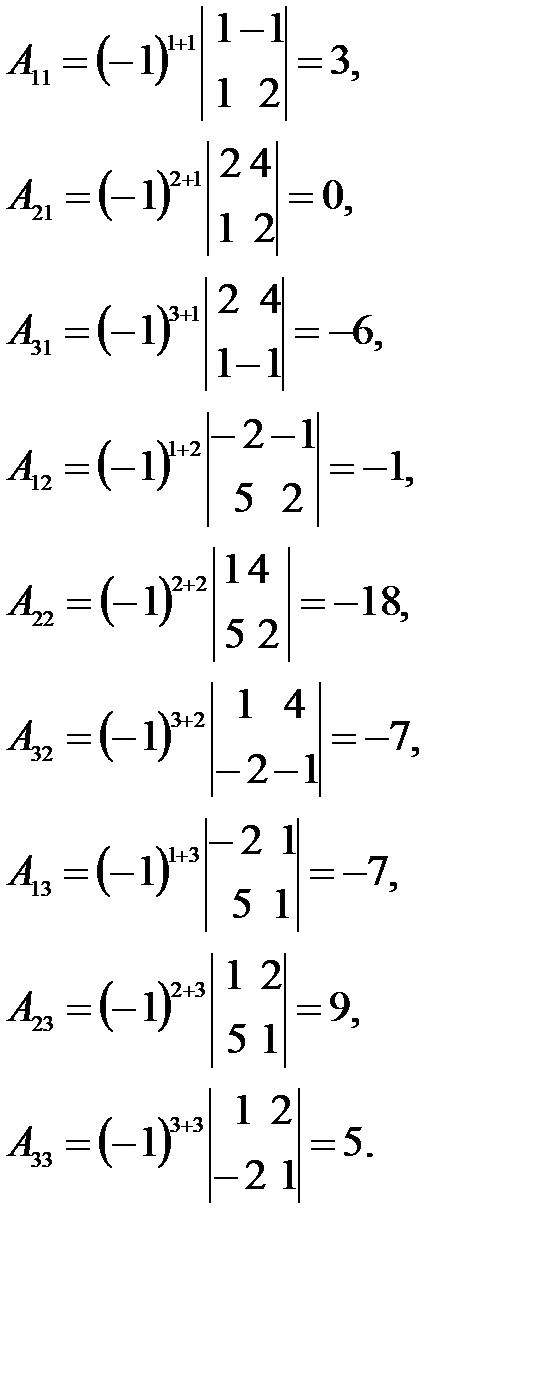
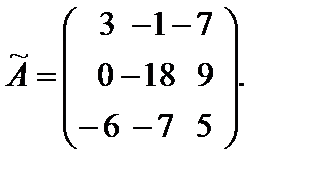Обратная матрица 
.
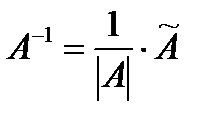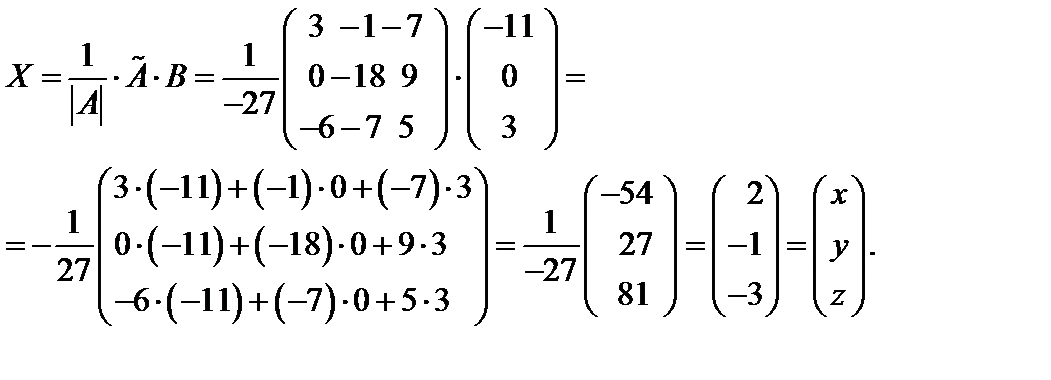
Из последнего равенства матриц получим: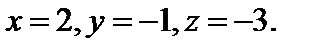 
Задачи для самостоятельной работы
В задачах 1-3 найти матрицу Х, удовлетворяющую данному уравнению:
1. 
.
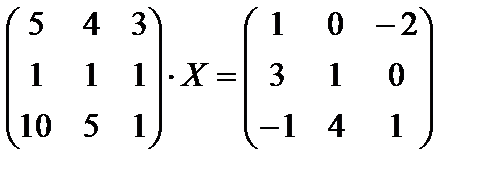2. 
.
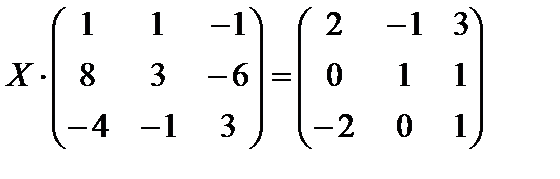3. 
.
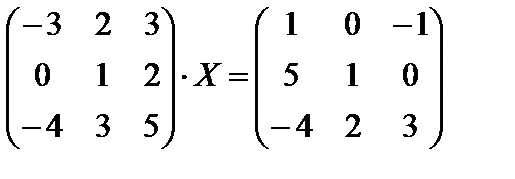Решение системы линейных алгебраических уравнений методом Гаусса.
Пример15. Решить систему линейных уравнений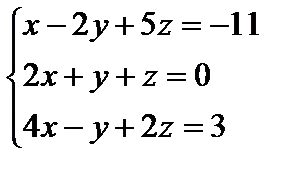
методом Гаусса:
Решение. С помощью следующих преобразований: а) перестановка строк, б) умножение строки на любое не равное нулю число, в) прибавление к данной строке произвольной линейной комбинации других строк, приведём расширенную матрицу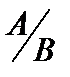 
к ступенчатому виду, при котором первые элементы любой строки (начиная со второй) – нулевые, и у каждой последующей строки число таких нулевых элементов хотя бы на один больше, чем у предыдущей.
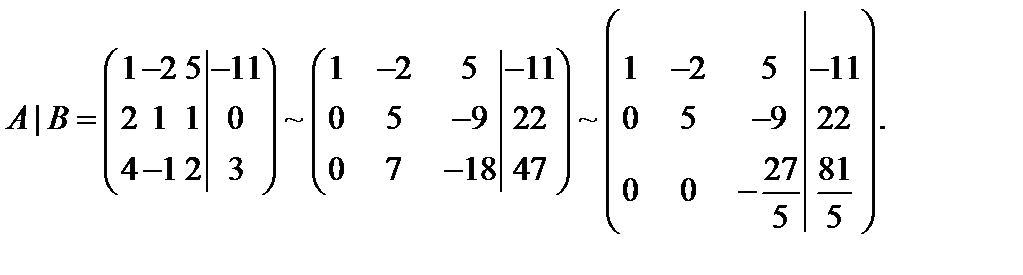
Вернёмся к линейной записи системы и методом исключения найдём x, y, z.
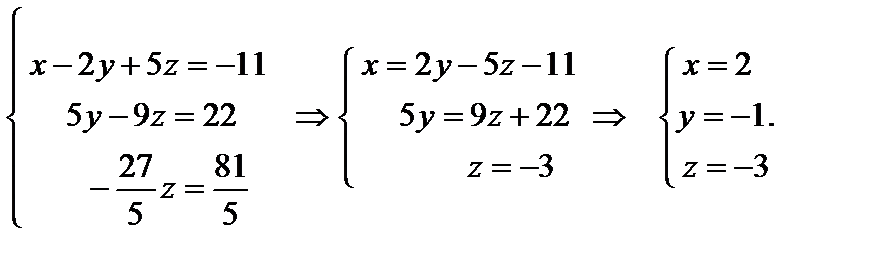
Ответ: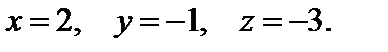 
▲
Задачи для самостоятельной работы
1. Решить систему по формулам Крамера и с помощью обратной матрицы:
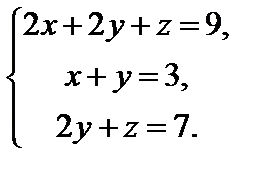
Решить системы линейных уравнений методом Гаусса:
2. 