РАЗДЕЛ 3.
ДИФРАКЦИОННЫЙ ИНТЕГРАЛ.
Анализ оптичесКОЙсхемы,
состоящей из транспаранта и линзы.
3.1 Дифракционный интеграл, основные положения, формулы.
Дифракционным интегралом называют интегральное преобразование, которое позволяет выразить распределение поля в некоторой области пространства через известное распределение поля на заданной поверхности. В частности, в когерентной оптике дифракционный интеграл применяется для того, чтобы выразить распределение амплитуд поля 
в плоскости П2, находящейся на расстоянии 
от плоскости П1, через распределение амплитуд поля 
в первой плоскости П1, т.е. через распределение поля на излучающей апертуре (рис3.1).
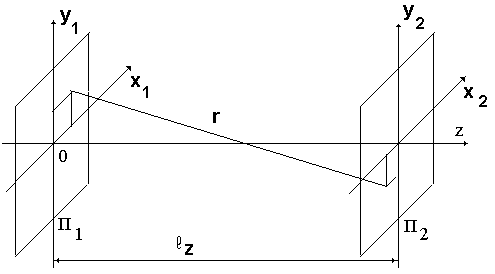
Рис 3.1 Схема, иллюстрирующая расчеты с помощью дифракционного интеграла.
При этом в оптических задачах учитывают ряд обстоятельств, которые значительно упрощают общий вид дифракционного интеграла.
-Излучающую поверхность (апертуру) обычно полагают плоской.
-Принимают во внимание то обстоятельство, что длина волны l оптического излучения очень мала по сравнению с расстоянием r от излучающей апертуры до области наблюдения и учитывают условие 
Это условие называют оптическим приближением.
-Используют так называемое параксиальное приближение, при котором полагают, что размер апертуры излучения мaл по сравнению с расстоянием между плоскостью апертуры и плоскостью наблюдения.
Дифракционный интеграл в точной формулировке был записан Кирхгофом в 1882 году. [1] Он явился точной формулировкой ранее выдвинутой идеи, называемой принципом Гюйгенса. Эта идея была развита Френелем. Напомним, что согласно принципу Гюйгенса каждая точка волновой поверхности может рассматриваться как самостоятельный точечный источник сферической волны.
С учетом определенных, упомянутых выше приближений, можно записать выражение для искомой функции распределения поля 
в плоскости П2 
на расстоянии 
от плоскости П1 (
, z = 0) через распределение поля 
в этой плоскости в виде:
, (3.1)
В этой формуле 
- площадь апертуры, ds – элемент площади dx 1, dy 1, r – текущий радиус вектор между точкой с координатами x 2, y 2 в плоскости П2 и точкой с координатами x 1, y 1 в плоскости П1 (рис. 4.1). При условии, что координаты x 1 и y 1, а также x 2, y 2 изменяются лишь в сравнительно небольшой ограниченной области, т.е. 
и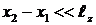 
, и аналогично 
, можно положить, что величина r изменяется очень мало. В этом случае мы не допустим большой ошибки, если положим, что в знаменателе дроби под интегралом в выражении (3.1) заменим переменную величину r на постоянную величину , которая является постоянной, не зависящей от переменных интегрирования. Выведем эту величину за знак интеграла, положив 
. В то же время следует заметить, что в показателе экспоненты такую замену сделать нельзя.
Величину r в показателе экспоненты представим в виде квадратного корня из суммы квадратов координат, который затем преобразуем с учетом предполагаемой малости отношений 
и 
:
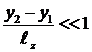. (3.2)
Из (3.1) и (3.2) получим следующее выражение, связывающее распределение комплексных амплитуд поля в плоскости П2 через распределение комплексных амплитуд в плоскости П1.
. (3.3)
Интересно отметить, что интеграл (3.3) представляет собой свертку функции распределения 
с функцией вида 
.
Формула (3.3) содержит в показателе экспоненты квадратичные члены и отражает случай так называемой дифракции Френеля.
3.2. Предельный переход к дифракции Фраунгофера.
В формуле (3.3) преобразуем разности квадратов в степени экспоненты подынтегрального выражения. Представим интеграл (3.3) в следующем виде:
(3.4)
В этом выражении множитель, содержащий в показателе экспоненты величины 
и 
вынесен за знак интеграла, так как х 2 и у 2 не являются переменными интегрирования. При некоторых условиях из подынтегрального выражения можно исключить множитель: 
Для этого необходимо чтобы показатель степени экспоненты был очень мал, т.е. чтобы выполнялись следующие условия:
. (3.5)
При этом 
Рассмотрим пример, когда апертура представляет собой квадратную площадку размером D. В этом случае величина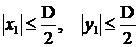 
, а наибольшие значения переменных x, y будут следующими: 
.
С учетом этого условия формулу (4.5) можно записать:
(3.6)
Отсюда следует условие
. (3.7)
Приближенно это условие записывают в виде:
. (3.8)
Это соотношение является условием перехода к дальней зоне поля излучения (по другой терминологии к зоне Фраунгофера). При этом интеграл (3.4) имеет следующий вид:
. (3.9)
Перед интегралом мы имеем ряд множителей. Группа множителей 
является константой, которая не зависит от координат х 2, у 2. Множитель 
является чисто фазовым, он описывает параболическую кривизну волнового фронта в плоскости 
.
Двойной интеграл по площади апертуры SA можно преобразовать к виду, который будет фактически преобразованием Фурье от распределения амплитуд поля на апертуре 
.
С этой целью: во-первых распространим пределы интегрирования на всю плоскость х 1 у 1, т.е. от 
до 
. Это можно сделать, так как за пределами апертуры поле излучения отсутствует 
при 
,
во-вторых: величины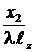 
и 
преобразуем следующим образом:
(3.10)
(3.11)
Эти приближения допустимы при малых величинах углов q1 и q2. Ранее мы приняли условие параксиального приближения, при котором углы дифракции, q1, q2 мы полагаем малыми. Тогда с учетом (3.10) и (3.11) можно записать:
. (3.12)
. (3.13)
Здесь x и h в соответствии с ранее данными определениями являются пространственными частотами.
В результате с учетом (3.12) и (3.13) интеграл (3.9) можно записать в виде:
. (3.14)
Интеграл в выражении (3.14) представляет собой двумерное преобразование Фурье распределения поля на апертуре.
Если мы поставим задачу исследовать распределение интенсивности (плотности мощности) в дальней зоне, то из выражения (3.14) получим
, (3.15)
т.е. распределение мощности излучения с точностью до постоянного множителя представляет собой спектр мощности излучения с апертуры.
Рассмотрим простой пример. Допустим, что плоская когерентная волна проходит через квадратное отверстие размером 1мм. на 1мм. Длина волны излучения равна 0,63 микрометра. Составим модель проведения эксперимента по наблюдению пространственного спектра мощности.
Найдем расстояние до области дальней зоны:
Расположим экран на расстоянии 
1,58 м. Например, расположим экран на расстоянии 4 метра от отверстия. Будем исследовать распределение плотности мощности излучения на экране. Напомним, что в результате анализа спектра дифрагированных волн, исходящих от щели с размером, равным D, ранее было получено выражение:
При условии, что апертура ограничена также и в направлении координаты Y
Получим: 
На экране мы увидим центральное пятно, обрамленное побочными максимумами в направлениях координат X и Y.
Рассчитаем координаты первых нулей 
и 
.
Положим 
. При этом 
, а 
. С учетом 3.12
получим: 
Аналогично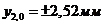 
3.3 Анализ оптической схемы из транспаранта и линзы.
3.3.1.Функция пропускания тонкой линзы. Для анализа нам необходимо будет описать функцию прозрачности линзы, т.е. функцию преобразования волнового фронта при прохождении его через тонкую линзу. С этой целью рассмотрим оптическую схему, изображенную на рис. 3.3.
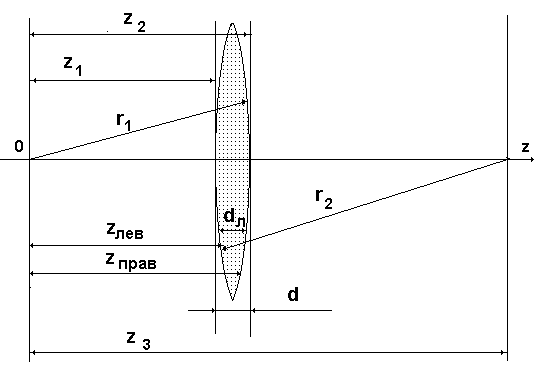
Рис 34. 3 Схема для расчета фазовой задержки оптической волны в линзе.
Тонкая линза, изготовленная из прозрачного материала с показателем преломления, равным 
, окружена воздухом с показателем преломления 
. Толщина линзы 
намного меньше, чем радиусы поверхностей r 1 и r 2, образующие линзу. Важное условие состоит в том, что материал линзы прозрачен и не поглощает излучения. При отсутствии поглощения линза представляет собой фазовый транспарант, функцию пропускания которого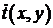 
можно выразить в виде:
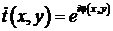(3.16)
Здесь функция 
отражает зависимость фазовой задержки оптической волны от координат x и y при ее прохождении от плоскости 
до плоскости 
(касательных плоскостей к выпуклостям линзы).
Проведем расчет фазовой задержки , которая складывается из фазовой задержки в толще материала линзы c показателем преломления и фазовой задержки в воздушных промежутках между поверхностями, образующими линзу, и плоскостями и . Толщину линзы d л (х, у) в произвольной точке с координатами х и у найдем рассчитав разность между координатами z правой и левой сферических поверхностей.
d л (х, у) = 
, (3.17)
где
, (3.18)
. (3.19)
Здесь z 3 – координата центра сферы с радиусом r 2 по отношению к точке x=0 расположения центра сферы с радиусом r 1.
Замена квадратного корня его приближенным разложением справедлива в случае параксиального приближения. При этом предполагается,
что 
. С учетом сделанных приближений толщина материала линзы составит:
d л (х, у) 
. (3.20)
Фазовая задержка световой волны с длиной волны l в материале
линзы составит:
. (3.21)
Фазовая задержка в воздушном промежутке 
между плоскостями 
и 
и поверхностями линзы составит:
, (3.22)
где d - расстояние между плоскостями и , а величина 
- длина воздушного промежутка.
Полный фазовый сдвиг световой волны при ее прохождении от плоскости до плоскости составит:
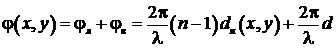. (3.23)
Второе слагаемое не зависит от координат х и у и фактически обозначает постоянный, не зависящий от координат фазовый сдвиг при прохождении волны от одной плоскости до другой. Поскольку этот сдвиг равносилен изменению начала отсчета световой волны, он не влияет на функции преобразования волнового фронта в оптической схеме, и его можно отбросить. После этого из формулы (3.23) с учетом (3.20) получим следующую формулу, выражающую зависимость фазового запаздывания волны в тонкой линзе от координат х. и у.
(3.24)
В этом выражении первое слагаемое также представляет постоянный фазовый сдвиг, не зависящий от переменных x, у. Отбросив это слагаемое, получим:
(3.25)
Из геометрической оптики известно соотношение, связывающее
оптическую силу линзы Dл с радиусами сферических поверхностей, образующих линзу.
(3.26)
С учетом выражений (3.25) и (3.26) формулу, характеризующую комплексную функцию пропускания линзы (3.16) можно записать в такой форме:
(3.27)
Следовательно, тонкая линза является фазовым транспарантом, который преобразует волну с плоским фронтом (на входе слева) в волну с волновым фронтом в форме параболоида вращения.
3.4 Преобразование Фурье в оптической схеме с линзой.
Рассмотрим оптическую схему, изображенную на рис.3.4. Плоский транспарант расположен в плоскости P1. Комплексная функция пропускания транспаранта 
. В этой же плоскости расположена тонкая собирающая оптическая линза с фокусным расстоянием, равным f л. Систему, состоящую из транспаранта и линзы, просвечивают слева в направлении оси 0z плоской оптической волной с амплитудой а 0.
Рис.3.4. Схе ма расположения транспаранта и линзы.
Плоскость 
наблюдения оптической волны расположена справа от линзы на расстоянии, равном фокусному расстоянию линзы 
. Рассмотрим процесс преобразования волны при ее распространении от плоскости до плоскости . Выразим распределение комплексной амплитуды волны непосредственно за плоскостью P1 (в плоскости, которую обозначим 
), после прохождения плоской волны через транспарант и линзу. Для этого помножим функцию распределения волны на входе системы на функцию передачи транспаранта и функцию пропускания плоской линзы:
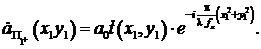(3.28)
Далее волна распространяется в свободном пространстве до плоскости наблюдения, которая находится на расстоянии 
. Для расчета поля 
в плоскости P2 при заданном распределении амплитуд в плоскости 
можно воспользоваться формулой дифракционного интеграла при малых углах дифракции (в параксиальном приближении).
Распределение 
тогда можно выразить:
(3.29)
Интегрирование в формуле (3.29) проводится по апертуре. Однако, учитывая, что за пределами рассматриваемой апертуры поле равно нулю (можно установить непрозрачный экран, окружающий апертуру), можно расширить пределы интегрирования от -µ до +µ.
Кроме того, преобразуем подынтегральное выражение, раскрыв квадраты разностей: 
и 
. После подстановки этих выражений в формулу (3.29) получим:
(3.30)
Введем некоторые обозначения:
. (3.31)
Углы q1 и q2 – между направлением на соответствующие точки с координатами х 2 и у 2 и осью 0z. Соотношения записаны в приближении малых углов q.
Заменив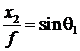 
и 
, мы получим:
(3.32)
Как видно формы выражений величин x и h совпадают с формой выражений для пространственных частот, которые мы рассматривали выше, в разделе 1. С учетом (3.32) выражение (3.30) принимает следующий вид:
(3.33)
Подчеркнутая часть выражения (3.33) является интегралом Фурье. Множитель перед интегралом состоит из постоянного сомножителя, не зависящего от 
и фазового множителя 
, отражающего кривизну волнового фронта в плоскости . Если рассматривать распределение интенсивности в плоскости P2(), то учитывая, что 
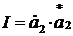, все мнимые сомножители перед интегралом при умножении их на комплексно сопряженные величины превратятся в единицы. Тогда распределение плотности мощности в фокусе линзы с точностью до постоянного множителя будет равно квадрату преобразования Фурье от распределения амплитуд в плоскости P1,
3.5. Пространственная фильтрация оптических волн и сигналов.
Поскольку в фокальной плоскости линзы формируется Фурье преобразование исходного распределения волнового фронта, то каждой координате фокальной плоскости линзы соответствует определенная пространственная частота. Если установить в фокальной плоскости непрозрачные экраны в определенных областях, соответствующих некоторым избранным пространственным частотам, то эти пространственные частоты будут исключены из спектра оптического сигнала. После этого скорректированный волновой фронт восстанавливается с помощью второй линзы, фокус которой совмещен с фокусом линзы, выполняющей преобразование Фурье. Таким образом, пространственная фильтрация в оптических схемах основана на замечательном свойстве линзы: она выполняет операцию преобразование Фурье оптического сигнала находящегося перед линзой, при переходе к фокальной плоскости линзы. Следует заметить, что в качестве фильтров в фокальной плоскости могут быть применены не только амплитудные фильтры (диафрагмы, экраны), но также и фазовые фильтры, изменяющие фазовый сдвиг оптической волны на определенных пространственных частотах. Далее рассмотрим некоторые примеры схем пространственной фильтрации.
3.5.1. Схема пространственной фильтрации волнового фронта с целью удаления оптических шумов, рис 3.5
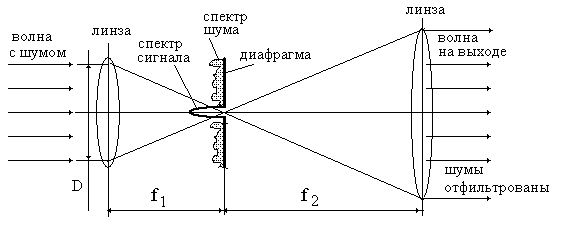
Рис.3.5. Схема пространственной фильтрации волнового фронта с применением круглой диафрагмы.
Положим, что идеальная исходная волна имеет плоский волновой фронт, однако, вследствие рассеяния на пылинках и неоднородностях предыдущих оптических элементов на плоском волновом фронте присутствуют случайные флуктуации амплитуды и фазы волны. Пространственный спектр флуктуаций обычно имеет большую ширину и расположен во всей частотной области от низких до высоких пространственных частот.
Пространственный спектр плоской волны, прошедшей через круглую апертуру с диаметром D представляет собой узкий пик диаметром главного максимума, равным:
. (3.34)
Здесь 
-это диаметр главного максимума распределения мощности излучения в фокальном пятне линзы (диаметр первого темного кольца в пятне Эйри), измеренный по нулевому уровню распределения мощности в фокальном пятне. Распределение интенсивности в пятне Эйри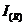 
выражается через функцию Бесселя: 
, где r- радиальная координата, a- радиус круглой апертуры, k- волновое число, 
интенсивность в центре пятна Эйри. При этом доля мощности излучения, сосредоточенной в пределах главного максимума пятна Эйри т.е. внутри первого темного кольца, составляет более 80%, а доля мощности излучения внутри второго темного кольца составляет более 90% полной мощности излучения., [М. Борн, Э. Вольф. Основы оптики. М. Наука 1970г. Глава 8, с.434]
Если диаметр диафрагмы равен или несколько больше диаметра , то основная доля мощности плоской волны пройдет через диафрагму и после прохождения через вторую линзу волна преобразуется в волну с волновым фронтом, с формой, близкой к плоской. При этом волновой фронт очищен от оптических шумов, так как спектральные составляющие шумов практически не проходят через диафрагму.
Пример расчета. Дано: диаметр пучка D=1мм., фокусное расстояние линзы 
=20мм. Рассчитаем диаметр центрального пятна при 
=0,6мкм.
На практике сложно изготовить подобную диафрагму установить ее с точностью порядка единиц микрометров. Поэтому на практике следует взять диафрагму с диаметром в 2-3 раза больше расчетного диаметра центрального пятна. При этом резко снижаются требования к точности установки диафрагмы, и несколько увеличивается доля мощности основного излучения. Вместе с тем, интегральная мощность шумов также увеличивается пропорционально площади отверстия.
3.5.2. Пространственная фильтрация с применением фазового фильтра. Метод фазового контраста.
В ряде случаев представляет интерес наблюдение и исследование фазовых объектов, у которых полезная информация заключена в пространственной фазовой модуляции транспаранта. Фазовая пространственная модуляция неразличима глазом при простом непосредственном наблюдении. Метод фазового контраста позволяет преобразовать фазовую модуляцию в амплитудную, которую легко можно наблюдать визуально. Оптическая схема, реализующая метод фазового контраста изображена на рис. 3.6. 
Рис.3.6. Схема пространственной фильтрации по методу фазового контраста.
Фазовый транспарант можно описать функцией вида:
(3.35)
Будем рассматривать эту задачу в приближении малой глубины фазовой модуляции, при этом можно записать: 
. С помощью первой линзы в оптической схеме выполняется преобразование Фурье при переходе из плоскости первой линзы к ее фокальной плоскости. Преобразование Фурье функции 
будет иметь вид:
(3.36)
Здесь функция 
является Фурье преобразованием функции модуляции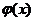 
. В плоскости пространственных частот эта функция распределена в широком диапазоне координат этой плоскости. В то же время функция 
сосредоточена в области нулевых координат фокальной плоскости.
Пространственный фильтр представляет собой прозрачную пластинку, в центральной части которой создано утолщение (а возможно и углубление), которое создает дополнительный фазовый сдвиг проходящей оптической волны на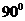 
по отношению ко всей остальной пластине. Напомним, что 
.Если отбросить постоянный фазовый сдвиг в прозрачной пластине, то воздействие фильтра на волну в фокальной плоскости будет выражаться следующими операциями. В выражении (3.36) первое слагаемое следует умножить на 
,
а второе слагаемое следует умножить на 1. В результате выражение, описывающее пространственный спектр на выходе фильтра примет вид:
(3.37)
Вторая линза выполняет обратное Фурье преобразование. В результате на выходе мы получаем следующее распределение:
(3.38)
Отбросив постоянный фазовый сдвиг на 90 градусов (т.е. ) на всей плоскости, мы видим, что функция 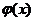представляет собой амплитудную модуляцию. В этом можно убедиться также, если найти распределение интенсивности, помножив выражение (3.38) на комплексно сопряженное выражение.
(3.39)
В результате мы показали, что рассмотренная здесь оптическая схема преобразует фазовую модуляцию в амплитудную. Схему можно применить для наблюдения и исследования фазовых, например биологических объектов.
3.6 Акустооптические схемы с линзами, предназначенные для оптической обработки радиосигналов.
Акустооптические схемы обработки радиосигналов могут выполнять операцию анализа спектра и операцию свертки радиосигналов, и обычно включают в себя три важных компонента:
· Пространственный модулятор когерентной световой волны, который преобразует функцию, описывающую радиосигнал, в соответствующую ей функцию пространственной модуляции волнового фронта световой волны, эту функцию выполняет акустооптическая ячейка, которая по существу преобразует радиосигнал в оптический сигнал;
· Линза, выполняющая преобразование Фурье оптического сигнала;
· Фотодиод или набор (линейка) фотодиодов, которые преобразуют оптический сигнал на выходе схемы в электрический сигнал на выходе схемы.
Пространственный модулятор. В качестве пространственного модулятора применяется акустооптическая (А.О.) ячейка. На рис 3.7 изображена схема А.О. ячейки, в которой используется эффект дифракции света на акустической (ультразвуковой) волне, т.е. схема дифракции Рамана-Ната. Возбудитель 1 представляет собой пластину, вырезанную из кристалла, обладающего пьезоэлектрическим эффектом или пластину из пьезокерамики. На обеих сторонах пластины нанесены металлические электроды. Возбудитель плотно связан со звукопроводом с помощью слоя индия или с помощью специального клея. Радиосигнал подается на электроды возбудителя ультразвуковых колебаний. Несущая частота радиосигнала находится в области резонанса механических колебаний возбудителя. При этом относительная ширина полосы частот возбудителя обычно велика, так как возбудитель сильно нагружен, и при этом значительная доля энергии колебаний передается в звукопровод. Колебания пластины возбуждают в звукопроводе бегущую со скоростью V акустическую волну. На противоположном конце звукопровода располагается поглотитель акустической волны, чтобы предотвратить помехи, которые может вызвать волна, отраженная от торца звукопровода.
Рис.3.7. Схема акустооптической ячейки, работающей в режиме
Рамана-Ната. 1- пьезоэлектрический возбудитель ультразвуковой волны,
2- звукопровод, 3-поглотитель ультразвуковой волны.
В результате прохождения через акустооптическую ячейку когерентная оптическая волна с длиной волны получает пространственную фазовую модуляцию в соответствии с радиосигналом, который подан на электроды возбудителя. Так, например, если сигнал имеет вид:
, (3.40)
то выражение, описывающее пространственную фазовую модуляцию волнового фронта оптической волны на выходе акустооптической ячейки, работающего в режиме Рамана-Ната, имеет вид:
(3.41)
Здесь 
- коэффициент, связывающий возмущения фазы волнового фронта с амплитудой сигнала.
Напомним, что режим Рамана-Ната имеет место при условии: 
В этом выражении мы использовали приближение малой амплитуды пространственной фазовой модуляции волнового фронта, вызванной акустической волной, так как при малых глубинах модуляции схема находится в линейном режиме. При малой амплитуде фазовой модуляции каждой частоте радиосигнала 
будет соответствовать определенный набор пространственных частот пространственного спектра и определенные углы направления дифракции первых порядков:
(3.42)
Схема акустооптического анализатора спектра радиосигналов.
Рис.3.8. Схема акустооптического анализатора спектра радиосигналов.
Положим, что в схеме акустооптического анализатора спектра, (рис.3.8), на вход возбудителя подан монохроматический радиосигнал с частотой . В звукопроводе возбуждается акустическая волна с длиной волны 
. В результате формируется дифрагированная оптическая волна, направленная под углом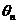 
:
(3.43)
Эта волна дает отклик на плоскости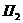 
в виде дифракционного пятна в точке с координатой, которую в приближении малых углов дифракции можно выразить формулой:
(3.44)
Каждой частоте соответствует точка на плоскости 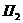. В этих точках расположены фотодетекторы, и с выхода каждого из фотодетекторов снимают электрический сигнал, соответствующий частоте .
Оценим предельную разрешающую способность данного анализатора. Размер дифракционного фокального пятна можно оценить как
(3.45)
Здесь D- поперечный размер оптического пучка, k- коэффициент который может быть порядка 1.
При практическом конструировании схемы желательно, чтобы размер фокального пятна и размер фотодетектора совпадали. Положим, что расстояние между соседними фотодетекторами составляет величину порядка размера фокального пятна, 
. Тогда, из 3.44 и 3.45 можно получить:
(3.46)
Здесь 
- время прохождения акустической волны через апертуру оптического пучка.
Проведем простую количественную оценку. Пусть в качестве материала звукопровода выбран плавленый кварц. Скорость распространения продольной звуковой волны составляет 
м/c. При размере апертуры D=1см, 
1,6 мкс и при k=1,22 получим 
.
Важным параметром устройства является число разрешаемых точек в пределах рабочего диапазона. Диапазон частот, в котором может работать данная схема, ограничена полосой частот возбудителя акустических волн. Полоса частот 
составляет некоторую долю (порядка 20-30%) от центральной резонансной частоты. Зная можно оценить число разрешаемых точек N:
(3.47)
Если 
60мГц, а 
, то число N=100. В последней формуле можно подставить полосу в мегагерцах, а длительность в микросекундах.
Важной особенностью схемы акустооптического анализатора спектра радиосигналов является очень малое время, необходимое для получения результатов. Практически оно составляет величину порядка , т.е. порядка времени прохода акустической волны через звукопровод. В подобных случаях принят термин: «анализ в реальном масштабе времени».
Схема, выполняющая операцию свертки двух радиосигналов(конвольвер).
Рис.3.9. Схема акустооптического конвольвера (схема Ван дер Люгта).
Имеются два сигнала.
Сигнал1 (входной):
(3.48)
Сигнал 2 (опорный):
(3.49)
Здесь 
- несущая частота сигналов. 
и 
- функции модуляции сигналов, т.е. огибающие несущей частоты.
В результате обработки этих сигналов схемой 3.9 можно получить функцию свертки данных сигналов, или их огибающих, т.е. функцию вида:
(3.50)
Следует заметить, что операция свертки во временной области для некоторого класса сигналов соответствует операции оптимальной фильтрации в частотной области. В общем случае для оптимальной фильтрации сигнала необходимо произвести операцию корелляции его с опорным сигналом.
Схема конвольвера, изображенная на рис 3.9, выполняет задачу получения на выходе схемы некоторого электрического сигнала, пропорционального свертке двух входных сигналов, поданных на акустооптические ячейки.
Схема содержит две акустооптические ячейки, которые расположены последовательно по ходу оптического пучка, просвечи