МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Группировка – это разделение единиц изучаемой совокупности на однородные группы по определенным, существенным для них признакам в целях выделения типов явлений, изучения структуры и взаимосвязей.
Основание, по которому производится группировка, называется группировочным признаком.
В соответствии с функциями группировки различают следующие ее виды:
1. Типологическая – это разделение всей совокупности на качественно однородные группы и выявление на этой основе экономических типов явлений.
2. Структурная – это составление характеристики структуры явления и структурных сдвигов.
3. Аналитическая - это исследование взаимосвязей варьирующих признаков в пределах однородной совокупности.
Факторным называется признак, оказывающий влияние на изменение результативных. Результативным называется признак, изменяющийся под влиянием факторных.
В практике проведения статистического исследования, для определения количества групп, наибольшее распространение получила формулы СТЕРДЖЕССА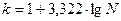
или 
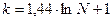где k - число групп; N- число единиц совокупности. После определения числа групп необходимо определить интервалы группировки. Интервал - это значения варьирующего признака, лежащие в определенных границах. Нижней границей интервала называется минимальное значение признака в интервале и наоборот. Величина (ширина) интервала - разность между верхней и нижней границами интервала. Интервалы группировки в зависимости от их величины бывают равными и неравными. Неравный интервал – применяется в тех случаях, когда размах вариации признака в совокупности велик и значения признака варьируют неравномерно. Неравные интервалы делятся на прогрессивно возрастающие, прогрессивно убывающие, произвольные и специализированные. Величина равного интервала определяется по следующей формуле: 
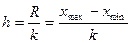где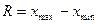 
- размах вариаци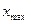и. 
и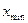 
- соответственно наибольшее и наименьшее значения признака в изучаемой совокупности; k – число групп. Величина интервалов, изменяющихся в арифметической прогрессии, определяется по формуле: 
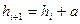в геометрической прогрессии: 
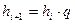где а - константа - число, которое будет положительным при прогрессивно возрастающих интервалах и наоборот. q - константа - положительное число, которое при прогрессивно возрастающих интервалах будет больше 1 и наоборот.Иногда имеющуюся группировку необходимо несколько изменить: объединить ранее выделенные относительно мелкие группы в небольшое число более крупных, типичных групп или изменить границы прежних групп с тем, чтобы сделать группировку сопоставимой с другими. Такая переработка результатов первичной группировки называется перегруппировкой или вторичной группировкой. Сводка - это подсчет числа единиц в подгруппах и группах, выделенных при группировке, и подведение итогов по количественным признакам.
Вариация – различие значений признака у отдельных единиц изучаемой совокупности в один и тот же период или момент времени.
К абсолютным показателям вариации относятся:
1. Размах вариации характеризует границы вариации изучаемого признака и определяется по формуле
Rвар =xmax - xmin
Размах вариации показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака.
2. Среднее линейное отклонение показывает, на какую величину отклоняется признак в изучаемой совокупности от средней величины признака, и определяется по следующим формулам:
· простое:
где n – число наблюдений признака;
· взвешенное:
Этот показатель учитывает только положительные отклонения.
3. Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по следующим формулам::
· простая:
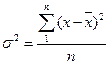или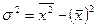 
.
· взвешенная:
4. Среднее квадратическое отклонение представляет собой обобщающую характеристику размеров вариации признака в совокупности и определяется по следующим формулам:
· простое:
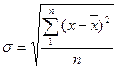
· взвешенное:
Среднее квадратическое отклонение показывает, на какую величину в среднем значение признака отличается от стандартного значения, и выражается в тех же единицах измерения, что и признак.
К относительным показателям вариации относятся:
1. Коэффициент осцилляции:
2. Линейный коэффициент вариации:
3. Коэффициент вариации:
.
Коэффициент вариации применяют для сравнительной оценки вариации, а также для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.
Важный вид средних величин – структурные (непараметрические) средние. Их используют для изучения внутреннего строения и структуры рядов распределения значений признака. К данным характеристикам относятся мода (Мо), медиана (Ме).
Мода (Мо) представляет собой значение изучаемого признака, повторяющегося с наибольшей частотой.
Медианой (Ме) называется значение признака, приходящегося на середину ранжированной (упорядоченной) совокупности.
В дискретном вариационном ряду определение медианного значения признака сводится к определению номера медианной единицы ряда по формуле:
где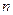 
– объем совокупности.
Полученное значение показывает, где точно находится номер медианной единицы (номер середины ряда).
Расчет моды и медианы для интервальных вариационных рядов производится по формулам:
– нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);
i – величина модального интервала;
– частота модального интервала;
– частота интервала предшествующего модальному и следующего за модальным соответственно.
где – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);
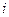- величина медианного интервала;
– накопленная частота интервала, предшествующего медианному;
- частота медианного интервала.
Тема. Выборочное наблюдение
Под выборочным наблюдением понимается такое не сплошное наблюдение, при котором статистическому наблюдению подвергаются единицы статистической совокупности, отобранные случайным образом.
Главная цель выборочного наблюдения - по результатам обследования части статистической совокупности дать характеристику всей совокупности в целом.
Совокупность отобранных для обследования единиц в статистике принято называть выборочной, а совокупность единиц, из которых производится отбор - генеральной.
Обозначения основных характеристики параметров генеральной и выборочной совокупности приведены в таблице16.
Основные характеристики генеральной и выборочной совокупностей
| Характеристика | Генеральная совокупность | Выборочная совокупность |
| Объем совокупности (численность единиц) | N | n |
| Численность единиц, обладающих обследуемым признаком | M | m |
| Доля единиц, обладающих обследуемым признаком |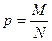 
| 
|
| Средний размер признака | 
| 
|
| Дисперсия количественного признака | 
| 
|
| Дисперсия доли |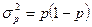 
| 
|
Предельная ошибка выборочного наблюдения:
; 
,
где 
- предельная ошибка средней;
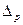- предельная ошибка доли;
- величина средней квадратической стандартной ошибки;
t - коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки.
Математиком А.М. Ляпуновым составлены специальные таблицы, связывающие коэффициент доверия t с вероятностью того, что разность меду выборочной и генеральной средними не превысит значения средней ошибки выборки μ.
t= 1 F(t) = 0,683 t= 1,5 F(t) = 0,866
t= 2 F(t) = 0,954 t= 2,5 F(t) = 0,988
t= 3 F(t) = 0,997 t= 3,5 F(t) = 0, 999
Зная выборочную среднюю величину признака 
и предельную ошибку выборки 
, можно рассчитать границы (пределы), в которых заключена генеральная средняя:
.
Доверительные интервалы для генеральной доли:
.
| Способ отбора единиц | ||
| повторный | бесповторный | |
| Формулы ошибок простой случайной выборки | ||
| Средняя ошибка μ: для средней для доли | 
| 
|
| Предельная ошибка Δ: для средней для доли | 
| 
|
| Формулы для определения численности простой случайной выборки | ||
| Численность выборки (n) | Способ отбора единиц | |
| повторный | бесповторный | |
| Для средней | 
| 
|
| Для доли | 
| 
|
Необходимый объем выборки для некоторых способов формирования выборочной совокупности
| Вид выборочного наблюдения | Повторный отбор | Бесповторный отбор |
| Собственно-случайная выборка: при определении среднего размера признака; при определении доли признака |
|
|
| Механическая выборка | То же | То же |
| Типическая выборка: при определении среднего размера признака; при определении доли признака |
|
|
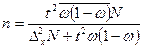
| Серийная выборка: при определении среднего размера признака; при определении доли признака |
|
|
Тема. Ряды динамики
Ряды динамики представляют собой ряды изменяющихся во времени значений статистического показателя, расположенного в хронологическом порядке.
В зависимости от качественной особенности изучаемого явления, а также вида исходных данных ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.
При формировании системы показателей изменения уровней ряда динамики принято сравниваемый уровень называть отчетным, а уровень, с которым производят сравнение – базисным.
Показатели динамики
| Показатель | Метод расчета | |
| цепные | базисные | |
| Абсолютный прирост | 
| 
|
| Коэффициент роста | 
| 
|
| Темп роста | 
| 
|
| Темп прироста | 
| 
|
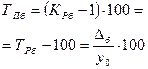
| Абсолютное значение 1% прироста | 
| 
|
К некоторым показателям изменения уровней ряда динамики относятся.
1. Абсолютный прирост показывает, на сколько в абсолютном выражении уровень текущего периода больше (меньше) базисного.
2. Коэффициент роста показывает, во сколько раз уровень текущего периода больше (или меньше) базисного.
3. Темп роста – это коэффициент роста, выраженный в процентах; он показывает, сколько процентов уровень текущего периода составляет по отношению к уровню базисного периода.
4. Темп прироста – показывает, на сколько процентов уровень текущего периода больше (или меньше) уровня базисного периода.
5. Абсолютное значение 1% прироста показывает, какая абсолютная величина скрывается за относительным показателем – одним процентом прироста.
Начальным этапом выделения и анализа тренда является проверка гипотезы о существовании тренда. Для отображения основной тенденции развития социально – экономических явлений применяются полиномы различной степени, экспоненты, логистические кривые и другие функции.
Средние показатели динамики
| Показатель | Метод расчета |
| 
|
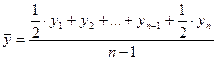
|  или 
|
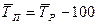|  , или
 ; 
|
| 
|
|  или 
|
| 
|
Полиномы имеют следующий вид:
- Полином первой степени - 
;
- Полином второй степени - 
;
- Полином третьей степени - 
;
- Полином n – степени - 
,
где 
- параметры полиномов;
t – условное обозначение времени.
Тема. Индексы
В статистике под индексом понимается относительный показатель, который выражает соотношение величин какого - либо явления во времени, в пространстве или сравнение фактических данных с любым эталоном.
Индивидуальный индекс физического объема продукции:
Индивидуальны индекс цен характеризует изменение цены одного определенного товара в текущем периоде по сравнению с базисным:
Индивидуальный индекс себестоимости единицы продукции:
Производительность труда может быть измерена количеством продукции, производимой в единицу времени (v), или затратами рабочего времени на производство единицы продукции (t). Поэтому можно построить:
• Индекс количества продукции, произведенной в единицу времени
• Индекс производительности труда по трудовым затратам
Индивидуальный индекс стоимости продукции (товарооборота) отражает, во сколько раз изменилась стоимость какого - либо товара в текущем периоде по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости товара, и определяется по формуле
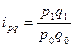
Агрегатный индекс – сложный относительный показатель, который характеризует среднее изменение социально – экономического явления, состоящего из несоизмеримых элементов.
К агрегатным индексам относятся:
Индекс физического объема продукции – это индекс количественного показателя. В этом индексе индексируемой величиной будет количество продукции в натуральном выражении, а весом – цена.
Формула для расчета индекса имеет вид 
Разность числителя и знаменателя (
) показывает, на сколько рублей изменилась стоимость продукции в результате роста (уменьшения) ее объема.
Индекс цен - показывает, во сколько раз возросла (уменьшилась) стоимость продукции из–за изменения цен, или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения цен.
Формула для определения индекса цен имеет вид:
Индекс стоимости продукции, или товарооборота (
) представляет собой отношение стоимости продукции текущего периода (
) к стоимости продукции в базисном периоде (
) и определяется по формуле:
Разность числителя и знаменателя (
) показывает, на сколько рублей увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным.
Как отмечалось ранее, стоимость продукции можно представить как произведение количества товара на его цену. Такая же зависимость существует и между индексами стоимости, физического объема и цен
Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов.
Зависимость для определения среднего арифметического индекса физического объема продукции будет иметь вид:
Так как 
, то формула этого индекса легко преобразуется в полученную ранее формулу:
К ним относятся: индекс переменного состава, индекс постоянного состава и индекс структурных сдвигов
Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени.
Например, индекс переменного состава себестоимости продукции одного и того же вида рассчитывается по формуле:
где 
– индекс переменного состава.
Индекс постоянного (фиксированного) состава – это индекс, исчисленный с весами, зафиксированными на уровне одного какого либо периода, и показывающий изменение только индексируемой величины. Например, индекс фиксированного состава себестоимости продукции рассчитывается по формуле: 
где Iфс – индекс фиксированного состава.
Под индексом структурных сдвигов понимают индекс, характеризующий влияние изменения только структуры изучаемого явления на динамику среднего уровня этого явления. Например, индекс изменения среднего уровня себестоимости определяется по формуле
где где Iстр – индекс структурных сдвигов.
1 вариант
1. Известны следующие данные по основным показателям деятельности предприятий.
| Номер предприятия | Объем продукции, тыс. руб. | Среднегодовая стоимость основных фондов, тыс. руб. | Среднесписочное число работников, чел. |
| 7,2 | |||
| 11,6 | |||
| 15,6 | |||
| 7,6 | |||
| 16,0 | |||
| 22,0 | |||
| 8,4 | |||
| 18,8 | |||
| 9,2 | |||
| 13,2 | |||
| 21,0 | |||
| 14,0 | |||
| 19,0 | |||
| 11,0 | |||
| 14,8 | |||
| 23,0 | |||
| 15,6 | |||
| 10,0 | |||
| 19,8 | |||
| 12,4 |
Произведите группировку предприятий с равными интервалами по стоимости основных фондов. Определите по каждой группе число предприятий, объем продукции, среднегодовую стоимость основных фондов, среднесписочное число работников. Результаты оформите в виде статистической таблицы. Сформулируйте выводы.
2. Имеются следующие данные о возрастном составе группы студентов заочного отделения (лет):
Требуется:
1) построить интервальный ряд распределения;
2) дать его графическое изображение в виде гистограммы и кумуляты;
3) определить численное значение моды и медианы для дискретных и интервальных рядов распределения;
4) по результатам группировки рассчитать абсолютные и относительные показатели вариации
Сделать выводы.
3. На 100 предприятиях, отобранных в порядке механического отбора, обследованы затраты труда на производство одного из изделий. Было установлено, что средние затраты труда на это изделие составляют 120 чел.-ч. при среднем квадратическом отклонении, равном 15 чел.-ч.
Определите с вероятностью 0,954 пределы средних затрат труда на одно изделие по всем предприятиям.
4. Имеется следующий ряд динамики среднемесячной номинальной начисленной заработной платы по Республике Бурятия, руб.
| Год | 2003 г. | 2004 г. | 2005 г. | 2006 г. | 2007 г. | 2008 г. |
| Среднемесячная номинальная начисленная заработная плата |
Определите средний уровень номинальной начисленной заработной платы; абсолютный прирост (базисный, цепной), темп роста (базисный, цепной), темп прироста (базисный, цепной), абсолютное значение 1% прироста; среднегодовой абсолютный прирост, среднегодовой темп роста и прироста, среднюю величину абсолютного значения 1% прироста. Результаты расчетов оформите в таблице и сформулируйте выводы.
5. Имеются следующие данные:
| Вид акций | Курс акций, руб. | Количество, шт. | ||
| Базисный | Отчетный | Базисный | Отчетный | |
| Простые | ||||
| Именные |
Рассчитайте: общий индекс товарооборота; общий индекс цен; общий индекс физического объема продаж.
2 вариант
1. Известны следующие данные по основным показателям деятельности предприятий.
| Номер предприятия | Объем продукции, тыс. руб. | Среднегодовая стоимость основных фондов, тыс. руб. | Среднесписочное число работников, чел. |
| 7,2 | |||
| 11,6 | |||
| 15,6 | |||
| 7,6 | |||
| 16,0 | |||
| 22,0 | |||
| 8,4 | |||
| 18,8 | |||
| 9,2 | |||
| 13,2 | |||
| 21,0 | |||
| 14,0 | |||
| 19,0 | |||
| 11,0 | |||
| 14,8 | |||
| 23,0 | |||
| 15,6 | |||
| 10,0 | |||
| 19,8 | |||
| 12,4 |
Произведите группировку предприятий с равными интервалами по объему произведенной продукции. Определите по каждой группе число предприятий, объем произведенной продукции, среднегодовую стоимость основных фондов, среднесписочное число работников. Результаты оформите в виде статистической таблицы. Сформулируйте выводы.
2. Имеются следующие данные о часовой интенсивности движения посетителей торгового центра (чел./ч):
Требуется:
1) построить интервальный ряд распределения;
2) дать его графическое изображение в виде гистограммы и кумуляты;
3) определить численное значение моды и медианы для дискретных и интервальных рядов распределения;
4) по результатам группировки рассчитать абсолютные и относительные показатели вариации
Сделать выводы.
3. При обследовании бюджета времени студентов были учтены затраты времени на обед. Обследовано 60 студентов, отобранных в порядке случайной выборки. Из них: 5 студентов затратили на обед 21 мин., 10 студентов – 27, 30 студентов – 33, 12 студентов – 39, 3 студента – 45 мин.
Определите средние затраты времени на обед студентами с вероятностью 0,97.
4. Имеется следующий ряд динамики среднемесячной номинальной начисленной заработной платы по Республике Бурятия, руб.
| Год | 2003 г. | 2004 г. | 2005 г. | 2006 г. | 2007 г. | 2008 г. |
| Среднемесячная номинальная начисленная заработная плата |
Требуется на основе данных составить точечный прогноз на 2009г., произведя выравнивание по уравнению прямой. Сформулируйте выводы.
5. Имеются следующие данные:
| Вид акций | Курс акций, руб. | Количество, шт. | ||
| Базисный | Отчетный | Базисный | Отчетный | |
| Предприятие №1 | ||||
| Простые | ||||
| Именные | ||||
| Предприятие №2 | ||||
| Простые |
Рассчитайте: изменение среднего курса акций (индекс цен переменного состава); изменение среднего курса акций за счет изменения курса по каждому предприятию (индекс цен постоянного состава); изменение среднего курса акций за счет влияния изменения структуры продаж по предприятиям (индекс влияния структурных сдвигов).
3 вариант
1. Известны следующие данные по основным показателям деятельности предприятий.
| Номер предприятия | Объем продукции, тыс. руб. | Среднегодовая стоимость основных фондов, тыс. руб. | Среднесписочное число работников, чел. |
| 7,2 | |||
| 11,6 | |||
| 15,6 | |||
| 7,6 | |||
| 16,0 | |||
| 22,0 | |||
| 8,4 | |||
| 18,8 | |||
| 9,2 | |||
| 13,2 | |||
| 21,0 | |||
| 14,0 | |||
| 19,0 | |||
| 11,0 | |||
| 14,8 | |||
| 23,0 | |||
| 15,6 | |||
| 10,0 | |||
| 19,8 | |||
| 12,4 |
Произведите группировку предприятий с равными интервалами по среднесписочному числу работников. Определите по каждой группе число предприятий, объем продукции, среднегодовую стоимость основных фондов, среднесписочное число работников. Результаты оформите в виде статистической таблицы. Сформулируйте выводы.
2. Распределение населения по возрастным группам характеризуется следующими данными:
| Возраст, лет | 0-4 | 5-9 | 10-14 | 15-19 | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 | Итого |
| Числен-ность, тыс. чел. | 36,8 | 29,8 | 28,5 | 38,7 | 49,8 | 42,5 | 36,3 | 30,0 | 27,6 | 34,7 | 32,1 | 25,3 | 453,9 |
Определите:
1) размах вариации;
2) среднее линейное отклонение;
3) среднее квадратическое отклонение;
4) дисперсию;
5) коэффициент осцилляции;
6) линейный коэффициент вариации;
7) коэффициент вариации.
Оцените количественную однородность совокупности.
3. Случайная выборка 800 домохозяек в центре города и их опрос, проведенный утром, показали, что 450 из них хотели, чтобы торговый центр города был пешеходной зоной.
Определите доверительные пределы доли всех домохозяек, кто бы придерживался того же мнения (с вероятностью 90%).
4. Имеется следующий ряд динамики среднемесячной номинальной начисленной заработной платы по Республике Бурятия, руб.
| Год | 2003 г. | 2004 г. | 2005 г. | 2006 г. | 2007 г. | 2008 г. |
| Среднемесячная номинальная начисленная заработная плата |
Требуется на основе данных составить точечный прогноз на 2009г., произведя выравнивание по уравнению параболы второго порядка. Сформулируйте выводы.
5. По имеющимся данным рассчитайте индивидуальные цепные и базисные индексы валового сбора зерновых КФХ, на основе следующих данных, т.:
| 400,0 | 420,0 | 446,0 | 478,0 | 492,0 | 520,0 |
4 вариант
1. Известны следующие данные по основным показателям муниципальных образований Республики Бурятия в 2009 г.
| МО |
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-04-26 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |