ЛОЖНОСТЬ ЗАКОНА СОХРАНЕНИЯ КИНЕТИЧЕСКОГО МОМЕНТА
© Солоненко Андрей Михайлович
E-mail: solon_andree@mail.ru
Введение
Кинетическим моментом (моментом количества движения) материальной точки относительно неподвижной точки О называется вектор L, равный векторному произведению радиус-вектора материальной точки r на вектор p её количества движения:
L = r · p = r ·m v,
где m и v – масса и скорость материальной точки. Если материальная точка будет перемещаться прямолинейно (под материальной точкой мы имеем право подразумевать центр масс системы), то величина её кинетического момента выразится как
│ L │=L=r∙p·Sinα=ℓ·p (1),
где ℓ - плечо вектора р относительно неподвижной точки О (под вектором р мы имеем право подразумевать главный вектор системы тел), α –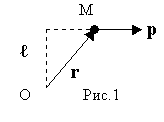 
угол между векторами r и р (см. рис.1).
Рассмотрим теорему об изменении p кинетического момента материальной точки так, как она обычно даётся в курсах теоретической механики, когда основное уравнение динамики F =d p /dt умножается векторно на r и представляется в виде следующего дифференциального уравнения:
r·F =d(r· m v)/dt - dr /dt · m v (2).
Затем догматично, т.е. бездоказательно утверждается, что для равных и параллельных векторов
d r /dt ·v = v·v =0 (3),
откуда получаем:
d L /dt= r·F = Mo (4).
Закон сохранения кинетического момента (ЗСКМ), основанный на выводе 4, гласит, что если главный вектор М ое момента внешних сил относительно неподвижной точки О (оси OZ) будет тождественно равен нулю, то кинетический момент такойсистемы не изменится с течением времени:
если М ое =о, то d L /dt =o и L =Const.
При этом в курсах механики утверждается, что внутренние силы изолированных систем не могут изменить ни количество движения, ни кинетический момент. Рассматривая выражение (1), мы найдем, что если под действием внутренних сил в изолированных системах изменится величина ℓ, то согласно ЗСКМ соответственно должно убывать или возрастать количество движения таких систем:
если L=ℓ∙p=Const., где ℓ≠Const., то и р ≠Const.
Отдельно же взятого доказательства того, что внутренние силы не могут изменить величину ℓ, в курсах механики не существует, что вызывает сомнение в справедливости вышеназванного закона как противоречащего закону сохранения количества движения. Далее, в научной литературе отсутствуют ссылки на экспериментальное доказательство ЗСКМ, отсутствие которых говорит, что ЗСКМ не проверялся специально поставленным экспериментом, что говорит о догматичности этого закона и также вызывает сомнение в его справедливости. Приводимые же в курсах механики примеры, якобы иллюстрирующие справедливость ЗСКМ – такие, как кувыркание акробатов, опыты со скамьей Жуковского и т.д. - не являются количественно точным доказательством, а лишь иллюстрируют изменение угловой скорости при изменении момента инерции вращающихся тел. Однако закон изменения угловой скорости в таких примерах может являться следствием закономерностей механики, не имеющих ничего общего с т.н. ЗСКМ - например, он может быть связанным просто с сохранением количества вращательного движения.
Часть1. Ревизия теоремы об изменении кинетического момента
1. Рассмотрим динамику горизонтально брошенного в поле тяжести Земли твёрдого тела массы mс начальной горизонтальной скоростью v 1.
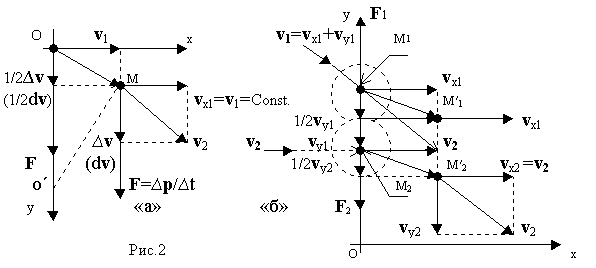
Положим, что в момент нахождения центра массы тела в точке О (начало декартовой прямоугольной системы координат, неподвижной относительно Земли, в которой мы будем рассматривать динамику тела) вектор v 1 был направлен вдоль оси OX, а затем начиная от точки О на тело начала действовать сила тяжести F = ∆p/∆ t≠o, проявляющая себя 2-м законом Ньютона, направленная параллельно оси OY (см. рис.2а, диссипативными силами и суточным вращением Земли пренебрегаем, а тело далее будем считать материальной точкой), при этом ее перемещение будет происходить в одной и той же плоскости, т.е. v z=o. Из сказанного следует, что перемещаясь из точки О в точку М материальная точка будет перемещаться криволинейно по параболе с ускорением, векторно направленным параллельно оси OY и за малый интервал времени ∆t = t2 - t1, где t = t1 = 0, пройдёт вертикальный путь, который определится как равный:
∆ y = F y∙(∆t)2/2m (1-1,1),
откуда следует, что:
∆ y /∆t= F y∙∆t/2m=∆ v y/2 (1,1-2)
Т.к. ускорение свободного падения g в близи поверхности Земли g =d v / dt= ∆ v/∆ t=Const, то
F y/m=∆ v /∆t=2∆ y /(∆t)2=d v у/dt=2d y /dt2 (1,1-3)
Взяв отношение вектора перемещения ∆ r = ∆x∙ i + ∆y∙ j = OM ко времени перемещения, мы получим среднюю скорость точки:
∆ r /∆t = ∆x∙ i /∆t + ∆y∙ j /∆t = v 1 + F ∙ ∆ t/2m = v 1+∆ v /2 (1,1-4),
где i и j – единичные базисные вектора. Точная же скорость точки в рассматриваемый момент времени t2 (точная скорость материальной точки в момент времени t1нам известна по условию), согласно 2-му закону Ньютона, определится как равная:
v 2 = v1 + F ∙∆t/m = v 1 + ∆v (1,1-5).
2. А теперь, не доверяя уравнению 2 (суть недоверия будет вскрыта несколько ниже), рассмотрим векторно-аналитически от чего будет зависеть изменение кинетического момента материальной точки (напомним, что под материальной точкой мы имеем полное право подразумевать центр масс системы тел, а применительно к вращательному движению – точку инерции, которая является точкой приложения главного вектора количества вращательного движения), имеющей в исходный момент времени t1 (начальный момент времени) вектор L = L 1= r 1· p 1= r 1·m v 1 данного момента. Для чего приложим к точке силу F = ∆p /Δt≠o и дадим приращения исходным параметрам исходного вектора L 1 , тогда согласно основополагающим азам дифференциального исчисления и согласно 2-му закону Ньютона:
L 1+ ∆L = (r 1+ ∆r)Ч(p 1+ ∆p) = L 2 (1,2-1),
где ∆r = v 1∙∆t + F ∙(∆t)2/2m, ∆ p = F ∙∆t (1,2-1a).
Раскрыв скобки выражения 1,2-1 и вычтя исходный вектор (L 2 -L 1=Δ L), при этом не пренебрегая т.н. малыми 2-го прядка, т.к. речь идет о законе количественного сохранения, который в теоретической механике приравнен к законам сохранения энергии и количества движения, и взяв отношения приращений ко времени приращения этих приращений, мы получим следующее количественно точное дифференциальное уравнение:
∆L /∆t = r 1 ·∆p/∆ t + (∆r·∆p)/ ∆t + ∆r /∆t ·p 1 (1,2-2).
Упростив (1,2-2) согласно (1,2-1а), найдём, что:
∆L/∆ t = r 1 ·F - (F ∙∆t/2m) ·p 1 (1,2-3).
Откуда следует, что если действие силы на точку будет удовлетворять условию М oе= r 1 ·F =о, а вектора F и р 1 будут непараллельными, то
∆ L /∆t= - (F ∙∆t/2m) ·p 1≠o и L ≠Const (1,2-4).
Из выражения (1,2-5), условно считая ∆t→o, найдём:
d L /dt = - (F ∙dt/2m) ·p 1 = - (F·p 1)∙dt/2m ≠ 0 и L ≠Const (1,2-5).
Если же модуль силы будет изменяться с течением времени, то левая часть выражения (1,2-4) выразится следующим образом:
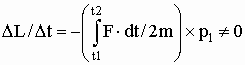(1,2-6).
Откуда следует, что при условии М o=0 кинетический момент материальной точки, вопреки утверждению теоретической механики, будет изменяться именно с течением времени!
Выражения (1,2-4) – (1,2-6) являются здравологическим следствием, вытекающим из 2-го закона Ньютона, и говорят об элементарной алогичности т.н. теоремы об изменении кинетического момента.
3. А теперь, ещё раз условно считая ∆t→o, из выражения (1,1-4) найдём, что:
d r /dt = dx∙ i /dt + dy∙ j /dt = dx∙ i /dt + F ∙dt/2m = v 1 + d v /2 (1,3-1).
Это меньшая по модулю скорость, чем (1,1-4), но также лишь средняя скорость точки, которую могут считать точной лишь представители ГАИ, пренебрегая приращением d v /2, но не представители теоретической механики, называющие её точной наукой! Точная же скорость точки в рассматриваемый момент времени t2 (точная скорость точки в момент времени t1 нам известна по условию), согласно 2-му закону Ньютона, определится как равная:
v 2 = v 1 + F ∙dt/m = dx∙ i /dt + 2dy∙ j /dt = v 1+d v (1,3-2),
где F ∙dt = d p ≠ 0 – элементарный импульс силы F =d p/ dt≠o за элементарный интервал времени dt≠o её действия.
Заметим также, что из приведённого примера, показанного на рис.2а, а также из уравнений (1,1-4) и (1,3-1), основанных на 2-м законе Ньютона, со всякой физико-математической и графической наглядностью следует, что если при ∆t→ o считать ∆y→dy=o, то это будет означать, что и ∆x→dx=o, т.к. приращения dx и dy приобретаются за одно и то же элементарное время dt. Но v 1 =v x≠o и F =d p /dt≠o по условию, а t1→t2 = dt≠o – это здравологическое понимание течения времени, которое не течёт вспять и которое ни на миг не остановишь, а следовательно, dx≠o и dy≠o!
4. Продолжим ревизию логических основ механики, для чего рассмотрим средний член уравнения (1,2-3), который, приняв во внимание (1,2-1а), предстанет в следующем виде:
(∆ r·∆p)/∆t = ∆r·F = v 1∙ ∆ t ·F = ∆x∙ i·F ≠ 0 (1,4-1)
или d r·F = v 1 ∙ dt ·F = dx∙ i·F ≠ 0 (1,4-1а)
как непараллельные вектора, где ∆x – это малое, а dx– элементарное плечо вектора F, приобретаемое им относительно, например, точек О и О′ (см. рис.2а).
А теперь, ещеёраз условно считая ∆t→o и исключив из уравнения (1,2-3) вектор (1,4-1), которым пренебрегают в курсах механики, составляя дифференциальное выражение (2) согласно общематематическому шаблону и при этом провозглашая закон количественного сохранения (Ньютон как основоположник дифференциального и интегрального исчислений прибегал к приёмам дифференцирования не в виде дифференциального исчисления как такового, т.е. не составлял шаблонов, но пользовался этим приёмом в отдельных конкретных случаях, индивидуально рассматривая каждый такой случай), мы получим следующее выражение:
d L /dt = d(r 1 · m v 1)/dt = r 1 ·F + d r /dt · m v 1 (1,4-2),
где, положив r 1= r, v 1= v, найдём, что (1,4-2) полностью идентично выражению 2. Из выражения (1,4-2) согласно догматическому утверждению (3) следует, что должно иметь место:
d r /dt = v 1 + F ∙dt/2m = dx∙ i /dt + dy∙ j /dt = dx· i /dt = v 1 ?! (1,4-3),
т.к. только в этом случае выражение
d r /dt ·v 1 = v 1 ·v 1 = 0 (1,4-3а)
будет представлять собой произведение действительно равных и параллельных векторов! А это будет означать согласно “логическим” основам механики, что:
F y = dp y/dt ≠ 0, но p y=Const !? (1,4-4).
Из сказанного следует, что абсолютно абсурдное (1,4-3), из которого вытекает (1,4-3а) или, что то же самое, утверждение (3), если действующая на точку сила F=dp/dt ≠ 0 выражается 2-м законом Ньютона, противоречит теоремам об изменении количества движения и кинетической энергии и не имеет с законами Ньютона, здраво логически отражающими законы природы, абсолютно ничего общего!
Предположим (условно), что догматическое утверждение 3 справедливо, тогда из (1,4-1а) (где выражение d r·F применимо и к вращательному движению) со всякой физико-математической наглядностью следует, что если М о= r 1 ·F =0, а вектора v 1 и F будут не параллельными, то d L/ dt = dx· i·F ≠ 0 и L ≠Const! Что в очередной раз иллюстрирует элементарную алогичность т.н. ”теоремы”.
5. Чтобы проиллюстрировать, что решение задач на основании вывода 4 количественно ошибочно, решим пример, показанный на рис.2а, на основании выражения (1,4-2) или, что то же самое, выражения 2, рассматривая кинетический момент горизонтально брошенного тела, которое мы условно считаем материальной точкой, поочередно относительно точек О и О′, и здесь ещё раз условно считая догматическое утверждение 3 справедливым, т.е. d r /dt ·p 1 = (v 1 + F ·dt/2m) ·p 1 = (F ∙dt/2m)· p 1 = (F /2m)·m v 1·dt = (F ·dx· i)/2 = 0 (1,5-1) как “параллельные” вектора, где F ≠ 0 и v 1≠0. По условию мы найдём, что:
а) относительно точки О, в которой L = L 1= r 1· p 1 = 0, т.к. r 1=OO=0, будем иметь согласно выводу 4 d L /dt = r 1· F = 0· F =0 и L =Const ?!
б) относительно точки О´, относительно которой L = L 1= r 1· p 1 ≠ 0, т.к. r 1=OґO ≠ 0, будем иметь согласно выводу 4 уже d L /dt = r 1· F = 0 как параллельные вектора (см. рис. 2а) и L =Const ?!
В действительности же момент силы тяжести, выражаемый 2-м законом Ньютона, относительно как точки О, так и О′ по истечении элементарного интервала времени, здровологически текущего к t2 (t1→t2 = dt≠o - напоминание для догматомыслящих), определится следующим выражением:
M o е = r 2· F = (r 1+d r)· F = d r · F = (v1 ∙dt + F ∙dt2/2m)· F = dx· i · F ≠ 0 (1,5-1а)
(см. пренебрегаемый ” теоретической механикой” вектор (1,4-1) и сравни с (1,5-1).
Из сказанного в пунктах (а) и (б), согласно алогизму 3 или, что по существу то же самое, согласно (1,5-1) следует, что кинетический момент горизонтально брошенного в поле тяжести Земли тела с начальной горизонтальной скоростью v 1 = v x ≠ 0 должен остаться неизменным !! Согласно же здравой физико-математической логике и практической действительности, как только материальная точка выйдет на элементарный шаг из точки О, вектор р 1 за счёт действия силы тяжести, проявляющей себя 2-м законом Ньютона F y=d p y/dt ≠ 0, приобретёт элементарное плечо dy=Fy∙dt2/2m ≠ 0 и соответствующую величину элементарного кинетического момента
dy∙p1 ≠ 0 (1,5-2).
В то же время материальная точка за счёт действия той же силы тяжести приобретёт дополнительное элементарное количество движения d p y= F y∙dt ≠ 0 (реализуется элементарный импульс силы), которое за счёт скорости v 1= v x приобретет элементарное плечо dx=v1∙dt, которое определит величину элементарного кинетического момента
dx∙F∙dt ≠ 0 (1,5-3)
(см. пренебрегаемое при дифференцировании теоретической механикой выражение 1,4-1). Причём
(dx∙dp)/(dy∙p1) = 2 (1,5-4),
где dp/m=d2y/dt=2dy/dt, a p1/m=dx/dt, что говорит о ложности вывода 4 в целом и о том, что решение задач на основании этого вывода является количественно ошибочным, и о том, что произведение т.н. малых 2-го порядка может быть больше малых 1-го порядка! А т.к. величины (1,5-3) и (1,5-4) разноимённые, то элементарное приращение кинетического момента материальной точки определится их разностью или, что то же самое, выражением (1,2-5) (отрицательный знак данного выражения не имеет принципиального значения, т.к. направление вектора L в целом условно).
Часть 2
В курсах теоретической механики, как уже говорилось во введении, утверждается, что внутренние силы изолированных систем не могут изменить ни количество движения, ни кинетический момент. Покажем ложность последнего утверждения, рассмотрев 2 примера.
1. Рассмотрим абсолютно упругий удар двух однородных шаров массы m1=m2=m, движущихся в изолированной неподвижной прямоугольной системе координат прямолинейно и поступательно со скоростями v1 =Const и v2 =Const, причём вектор v2 параллелен оси OX (см. рис.2б). Откуда следует, что в момент прихода центров шаров (центры масс шаров) в точки М1 и М2 произойдёт удар и возникнут силы действия и противодействия F 1 = - F 2, направленные вдоль линии, соединяющей центры шаров и вдоль оси OY. При этом вектор v1 разложится на 2 взаимно перпендикулярные составляющие v1 = v x1 + v y1 (индексы ‘’x’’ и ‘’y’’ далее будут указывать параллельность соответствующих векторов соответствующим координатным осям). Теоретическая механика, называя такой удар косым центральным (шары считаем гладкими, трением пренебрегаем), утверждает, что касательные составляющие скоростей, перпендикулярные линии удара, не изменяются: v x1=Const, v2 = v x2=Const. Составляющие же, направленные вдоль линии удара, изменяются так же, как при прямом ударе. Следовательно, после удара ударяющий шар, т.к. m1=m2, передаст свою скорость v y1= v y ударяемому шару v y2= v y1= v y.
Решая данный пример на основании уравнения (1,2-4) и применяя его к центру масс каждого отдельно взятого шара, мы найдём, что r 1· F 1,2 = 0 как параллельные вектора, где вектор r 1 для каждого шара - это вектора ОМ1 и ОМ2; а вектор р 1 – это вектора m1(v x1+ v y1) и m2vx2. Решая уравнение (1,2-4) далее, мы найдём, что:
∆ L 1/∆t = - (F y1∙∆t/2m)·m(v x1+ v y1) = - (F y1∙∆t/2m)·m v x1 ≠ 0 и ∆ L 2/∆t = - (F y2∙∆t/2m)·m v x2 ≠ 0 (2,1-1)
как непараллельные вектора. Окончательно же будем иметь:
∆ L/∆ t = ∆L 1 /∆ t - ∆L 2 /∆ t = 1/2 v y·m(v x2 - v x1) (2,1-2).
Откуда следует, что если v x1≠ v x2, то ∆ L ≠0 и L ≠Const – как правило, т.к. v x1= v x2 – это частный случай.
Исходя из того, что во время удара шары будут упруго деформированы, то силы F 1= F 2 будут действовать в течение некоторого интервала времени ∆t≠0, в течении которого при косом взаимодействии изменяется величина плеча ℓ≠сonst главного вектора количества движения данной системы, которыйравен p = p1 + p2 = Const., а L=ℓ∙p ≠ Const., о чём и говорилось в общелогическом замечании, приведённом во введении. Если же силы F 1 = - F 2 будут долгодействующими - например, шары будут долго испытывать взаимно действующее косое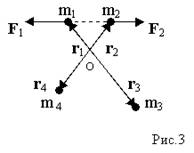 
отталкивание, то в этом случае вектор ∆ L ≠0 может быть сколь угодно большим.
2. А теперь рассмотрим следующую систему: две пары шаров массы m1, m3 и m2, m4 закреплены на двух стержнях, способных поворачиваться относительно неподвижной оси OZ так, что если мы приведём данную систему в движение, то центры масс шаров m1 и m2 начнут перемещаться по одной и той же окружности радиуса r1=r2, а центры шаров m3 и m4 - по окружностям r3≠r4 (см. рис.3, ось OZ перпендикулярна плоскости рисунка). Положим, что данная система удовлетворяет следующему условию:
m1∙r1 = m3∙r3 (2,2-1а) и m2∙r2 =m4∙r4 (2,2-1в).
А теперь положим, что между шарами массы m1 и m2, которые далее будем считать материальными точками, возникнут и начнут действовать внутренние силы отталкивания, до возникновения которых система находилась в состоянии покоя и которые, согласно законам Ньютона, будут удовлетворять следующему уравнению F 1= ∆p 1/∆t= F 2= ∆p 2/∆t. Под их действием шары со стержнями начнут поворачиваться, приобретая количество движения, малое приращение которого согласно (2,2-1а) и (2,2-1в) выразится 2-мя уравнениями: ∆p1,3=m1∙r1∙∆ω1=m3∙r3∙∆ω3 и ∆p2,4=m2∙r2∙∆ω2=m4∙r4∙∆ω4, где ∆ω1=∆ω3 и ∆ω2=∆ω4 – это малое приращение угловой скорости соответствующих шаров (трением пренебрегаем, сила тяжести направлена параллельно оси OZ, т.е. М ое=о, а стержни считаем невесомыми, несгибаемыми и нерастяжимыми). Из сказанного следует, что ∆ p 1=∆ p 2, т.к. F 1= F 2. Следовательно, ∆p1=∆p3=∆p2=∆p4=∆p, а это означает, что ∆L=∆p∙(r3 - r4) ≠ 0, т.к. r3≠r4 и L ≠Const. – как правило, т.к. r3=r4 – это частный случай. Если же считать ∆ L =0, то это будет означать, что F 1≠ F 2. То есть,как многократно говорилось и иллюстрировалось выше, т.н. ЗСКМ не имеет m1 m2 с законами Ньютона, за исключением F 1 F 2 демагогических деклараций, абсолютно r 1 r 2 ничего общего!
Вывод
Как уже говорилось во введении, ЗСКМ экспериментально не проверялся (Ньютон, основоположник механики, гипотез не измышлял), тогда как справедливость (1,1-1), откуда вытекает справедливость (1,1-4), откуда физико-математически последовательно вытекает справедливость (1.2-4), (1,2-5) и (1,2-6), доказана экспериментально. А это означает, что ложность т.н. “теоремы” и т.н. ”закона” можно считать доказанными экспериментально.
Логические же основы теоретической механики, в том числе так называемой небесной механики, нуждаются в дальнейшей ревизии.
Дата публикации: 30 сентября 2002
Источник: SciTecLibrary.ru