f(q,p,t)
До сих пор не существует единого, общего метода нахождения ФСР, пригодного для любых неравновесных систем. В связи с этим не развита общая аксиоматика статистической теории. Мы будем изучать равновесные системы. Равновесным называется стационарное состояние изолированной системы. Все макроскопические характеристики такой системы постоянны во времени:
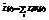

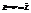
Чтобы макроскопические величины были постоянны, нужно чтобы ФСР не зависело от времени, все вероятности постоянны, плотность вероятности не содержат времени.
Wi=const f=f(q,p)
Общее наименование сохраняющейся величины ® ò движения. ФСР есть интеграл движения. Поэтому она может зависеть от координат и импульсов частиц только через другие сохраняющиеся величины
f(q,p)=f(J1(q,p), J2(q,p)…)
Jk=const какие-то другие ò движения.
Система из N частиц в самом общем случае может иметь N-1 ò движения
В статистической изике количество частиц обычно считается запертым в некотором объеме. Без ограничения общности этот сосуд можно считать неподвижным Þ импульс и момент импульса системы можно выпустить из числа ò движения, однако, есть дополнительный внутренний ò движения
Дополнительный постулат:
Для равновесных систем колличество частиц имеет один единственный ò движения – энергия системы, т.е.
f(q,p)=f(E(q,p)), причем E(q,p)=const
Поскольку энегрия одна и таже для всех микросостояний, все микросостояния равновесной системы оказываются равновероятными
Wi=A, где A какая-то константа одна и та же для всех микросостояний, она не изменяется с течением времени.
W=W(Е,N,l) обозначим через W полное число возможных микросостояний системы, она зависит от энергии, числа частиц и от внешних параметров.
|
|
Из условия нормировки:
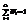 WA=1 получаем: A=1/W
WA=1 получаем: A=1/W 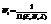 фундаментальный основной закон, ФСР для равновесной системы, она имеет специальное наименование микроканоническое распределение. В физику она была введена в 1901 г. Гиббсом.
фундаментальный основной закон, ФСР для равновесной системы, она имеет специальное наименование микроканоническое распределение. В физику она была введена в 1901 г. Гиббсом.
Словесное выражение этой формулы:
Все микросостояния равновесной системы равновероятны.
Дополнительное постулативное утверждение: из всех ò движения для системы имеет место только один – энергия системы
Данный постулат связан с предствавлением о полной неупорядоченности, хаотичности внутренного движения в равновесной системе.
Беспорядочность означает отсутствие всякой согласованности движения частиц. Нет никакой кореляции (согласованности) между координатами и импульсами частиц. Всякая упорядоченность, всякая согласованность любого дополнительного ò движения означает, что некоторые микросостояния для системы будут недоступны.
В формуле микроканонического распределения стоит W полное число возможных микросостояний, которые только возможны.
Ни на одно микросостояние, допустимых данных E,N,l нет запрета, никакое из них ничем перед другим не выделено, все они реализуются с одинаковой частотой. До настоящего времени ни одного исключения из микроканонического распределения не существует.
6. Связь энтропии с числом микросост. в локально-равновесных системах. Принцип Больцмана и ф-ла Больцмана. Статист. толкование закона созраст. энтропии. Пример примен. метода Больцмана. Согласно микро-канонич распределению для равновесной системы 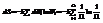
здесь W одинаковых слагаемых 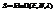 энтропия опр-ся числом возможных состояний системы. Всякое ограничение на движение ч-ц, всякая согласованность в движении ч-ц ¯WÞименно в равновесии энтропия имеет max. Время релаксации t (время установления равновесия) очень сильно зависит от размеров системы. Может оказаться так, что любая малая часть системы уже придет в равновесие, а вся система вцелом нет (лед-вода, электронная и ионная подсистемы мб в равновесии, а электронно-ионная система мб в неравновесии). Рассм изолир сист в кот м выделить большое кол-во квазинезавис равновесных подсистем. Для любой i части м опр-ть Ei,Ni,li. Соот-но м задать энтропию каждой малой части.
энтропия опр-ся числом возможных состояний системы. Всякое ограничение на движение ч-ц, всякая согласованность в движении ч-ц ¯WÞименно в равновесии энтропия имеет max. Время релаксации t (время установления равновесия) очень сильно зависит от размеров системы. Может оказаться так, что любая малая часть системы уже придет в равновесие, а вся система вцелом нет (лед-вода, электронная и ионная подсистемы мб в равновесии, а электронно-ионная система мб в неравновесии). Рассм изолир сист в кот м выделить большое кол-во квазинезавис равновесных подсистем. Для любой i части м опр-ть Ei,Ni,li. Соот-но м задать энтропию каждой малой части. 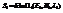 исп-ся аддитивность S=>
исп-ся аддитивность S=> 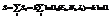 где W=PWi, для локально равновесной системы формально получается формула того же вида, что и для равновесной сист-ы.
где W=PWi, для локально равновесной системы формально получается формула того же вида, что и для равновесной сист-ы.
|
|
Равнов 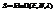 неравнов
неравнов 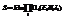 S(t),
S(t),
EiNili меняются с течением времени.
Малое взаимод-е с течением времени меняет энергию подсистемы. Обмен энергией и ч-ми идет ч\з теплообмен и диффузию, т е происходит беспорядочно, хаотически. S- локально- равновесной системы величина флюктуирующая не представляет генерального направления и S д со временем. Именно для изучения локально-равновесных сист широко исп-ся принцип, метод, фор-ла Б.
пр. Больцмана утверждает, что энтропия связана с вероятностью Макро-сост-я системы. (S означ-т вер-ти макро-сост) Конкретной реализацией явл-ся формула Больцмана S=klnWт, где Wт- ТД вер-ть М-сост-й. Метод Больцмана заключается в изучении систем на основе фор-лы Больцмана и соот-и Wт=W, где W-число м-сост-й, через которое реализуется данное М-сост-е. метод Больцмана: справедлива ф.Больцмана, если все м-сост-я равновероятны М-сост-я должны рас-ся ка случайные события данные условия берутся только для равновесных систем или локально-равновесной системы.
|
|
Имеется замкн система с постоянными внешн пар-ми и пост числом ч-ц. Разделим систему на 2 половинки и рассм состояние с различным распределением ч-ц по эт половинкам (сист равновесна, дв-е ч-ц абс беспорядочно)Wл=1/2, Wп=1/2 М посчитать, какова вер-ть того, что n- конкретных ч-ц нах-ся слева, а ост справа. Д указать положение ч-ы, т е имеем детальное описание сист. Если газ идеальный то вер-ть такого микросост= Wab...cd...=1/2n где n-любые молекулы. Все микросост равновер-ны
Согласно методу Больцмана ТД вер-ть = числу состояний, ч\з кот реализ-ся данное состояние.(2 круга сразными буквами). Речь идет о числе выборок n- объектов из N возможных.
Wт(n)=W(n)=CNn=N!/n!(N-n)! выражение имеет максимум при n=N/2, x=n- a, a =N/2 х-отклонение от равномерного распределения переходя от n к х. 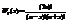 , предполагаем, что а>>1,x<<a. При выполнении неравенств WT@W(0)e-x2/a, при х=0 имеет max WT(0)=WTmax
, предполагаем, что а>>1,x<<a. При выполнении неравенств WT@W(0)e-x2/a, при х=0 имеет max WT(0)=WTmax
Вывод: микроскоп сост задано с точностью до флуктуаций, обычно флуктуациями м пренебречь, величина флук-й меньше точности измерений, прибры их не обнаруживают. Сколько нибудь заметные отклонения от равном распр-я имеют прак-и 0 верть по сравнению с равном распр-м ч-ц по обеим половинам.
Закон роста. Пусть в ансамбле есть распред. вероятн. по состоянию, которое изменяется со временем Wi(t). Можно ввести энтропию той же самой ф-лой что и для отд. системы. 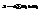 .
. 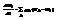 (это по стат. анс. Гиббса).
(это по стат. анс. Гиббса). 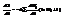 . Мы знаем что
. Мы знаем что 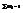 и
и 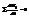 . =>
. => 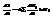 , подставляем
, подставляем 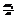 ,
, 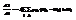 . (*). Меняем индекс суммирования. i«k. Получим (**). Получили 2 выражения для пр-ных. Сложим их (* и **) при усл. pik=pki.
. (*). Меняем индекс суммирования. i«k. Получим (**). Получили 2 выражения для пр-ных. Сложим их (* и **) при усл. pik=pki. 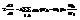 . Все справа
. Все справа  будет
будет 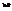 . Само
. Само 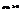 - т.к. вероятность перехода из одного состояния в другое. Но произведение тоже всегда +. Т.е.
- т.к. вероятность перехода из одного состояния в другое. Но произведение тоже всегда +. Т.е. 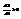 . (=0 при Wk=const). Т.о. закон возр. энтропии как-бы выводится на основании механики ансамбля систем. Это нельзя считать полным выводом, т.к. допущение – вер-ть для ансамбля систем отождествлена с распред. вер-тей для микросост. отдельной системы, а это фактически самостоят. постулат.
. (=0 при Wk=const). Т.о. закон возр. энтропии как-бы выводится на основании механики ансамбля систем. Это нельзя считать полным выводом, т.к. допущение – вер-ть для ансамбля систем отождествлена с распред. вер-тей для микросост. отдельной системы, а это фактически самостоят. постулат.
12. Распределение Максвелла-Больцмана. Распределение Максвелла и его свойства. Распределение для модуля скорости и энергии частицы. Распределение Больцмана. Барометрическая ф-ла. Изуч сист- класс идеал одноатомн газ мы будем считать для общности, что газ помещен во внешн силовое поле U(r), каждая частица газа связана с внешним полем отдельно самостоятельно. Поэтому U(r) есть потенциальная энергия одной частицы находящейся в точке r. Поставим вопрос как найти вер-ть того, что частица обладает имп-ом и находится в точке r. Используем каноническое распределение 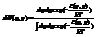 Записанное в таком виде оно отвечает на вопр какова вероят попадания в
Записанное в таком виде оно отвечает на вопр какова вероят попадания в  i=0,1,2..g. Число степеней свободы g велико, поэтому незнаем как выделить отсюда информацию об одной частице. Будем использовать обобщенные координаты
i=0,1,2..g. Число степеней свободы g велико, поэтому незнаем как выделить отсюда информацию об одной частице. Будем использовать обобщенные координаты 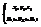
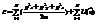 . Т к взаим-я м/у ч-ми нет, пот энергия может появиться только, если на газ наложено внешнее поле. С внешним полем каждая молекула взаим-т индивид-но. Энергия распадается на ряд слагаемых, которые зависят от коорд и имп-ов только одной частицы. Соответ экспонента распадается на
. Т к взаим-я м/у ч-ми нет, пот энергия может появиться только, если на газ наложено внешнее поле. С внешним полем каждая молекула взаим-т индивид-но. Энергия распадается на ряд слагаемых, которые зависят от коорд и имп-ов только одной частицы. Соответ экспонента распадается на 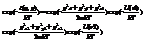 Это означает, что наше распределение по коорд и имп всех частиц распадается на произведения распредел коорд и имп отдел частиц Такое распадение возможно если отдельные частицы распред независимо др от др. В данном случае это отражает физику- взаимодействия между частицами на расстоянии нет и поэтому их можно рассматривать как квазинезависимые др по отнош к др. Поэтому мы легко можем из общего распред выписать распред для одной час-цы. В силу равноправия частиц они все имеют одинаковую стр-ру
Это означает, что наше распределение по коорд и имп всех частиц распадается на произведения распредел коорд и имп отдел частиц Такое распадение возможно если отдельные частицы распред независимо др от др. В данном случае это отражает физику- взаимодействия между частицами на расстоянии нет и поэтому их можно рассматривать как квазинезависимые др по отнош к др. Поэтому мы легко можем из общего распред выписать распред для одной час-цы. В силу равноправия частиц они все имеют одинаковую стр-ру 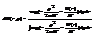 . Действительно нормировочный интеграл I тоже можно представ в виде произв множит однотипных с интегралом стоящим в послед форм-ле. Записанное распред наз-ся распред Максвелла-Больцмана, оно легко разбивается на 2 распр-я.
. Действительно нормировочный интеграл I тоже можно представ в виде произв множит однотипных с интегралом стоящим в послед форм-ле. Записанное распред наз-ся распред Максвелла-Больцмана, оно легко разбивается на 2 распр-я.
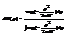
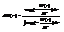 Т.е. имеются 2 независимых распред для коорд и имп. Физика- мы полагаем, что потенциальная энергия есть функц только коорд, а кинет в клас физике зависит только от имп и никогда от коорд. dW(p)- распред Максвелла, dW(r)- распред Больцмана. распределение Максвела: характерно своей универсальностью. Оно применимо не только к ид газу но и к любой сист точечных класич част. Потому что кинет энергия всегда зависит от импульсов..
Т.е. имеются 2 независимых распред для коорд и имп. Физика- мы полагаем, что потенциальная энергия есть функц только коорд, а кинет в клас физике зависит только от имп и никогда от коорд. dW(p)- распред Максвелла, dW(r)- распред Больцмана. распределение Максвела: характерно своей универсальностью. Оно применимо не только к ид газу но и к любой сист точечных класич част. Потому что кинет энергия всегда зависит от импульсов.. 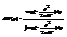 интеграл стоящий в знаменателе легко вычислить
интеграл стоящий в знаменателе легко вычислить 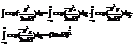 Þ
Þ 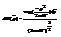 очень часто вместо импульса использ скорость
очень часто вместо импульса использ скорость 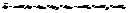
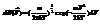 Максв распред можно считать статис незав. Распред-е по скоростям и энерг. Распр-е по имп-сам легко преобр в распр по скорост
Максв распред можно считать статис незав. Распред-е по скоростям и энерг. Распр-е по имп-сам легко преобр в распр по скорост 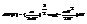 его можно предст-ть в виде произ-я трех распред-ий вероятности для проек-й скорости
его можно предст-ть в виде произ-я трех распред-ий вероятности для проек-й скорости 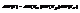
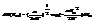 формула свидетельствует о статис незав-ти всех трех проекций скорости. В кл физике дв-е в свободном пространстве вдоль каждой оси не связано с движением вдоль др осей. тогда для модуля скорости получим
формула свидетельствует о статис незав-ти всех трех проекций скорости. В кл физике дв-е в свободном пространстве вдоль каждой оси не связано с движением вдоль др осей. тогда для модуля скорости получим 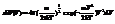
распределение для модуля скорости легко преобразовать в расп-е для энергии, если использовать 
(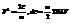 )то получим распред-е вероят-ей для значений энергии свободн частицы
)то получим распред-е вероят-ей для значений энергии свободн частицы 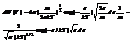 . Распред-е Больцмана В отличие от М. распред-я распределение Больцмана для каждой задачи будет свое т.к оно зависит от вида ф-ии U(r), т.е оно не универсально. 1)пот эн отсутст-т
. Распред-е Больцмана В отличие от М. распред-я распределение Больцмана для каждой задачи будет свое т.к оно зависит от вида ф-ии U(r), т.е оно не универсально. 1)пот эн отсутст-т 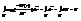 тогда
тогда 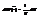 вид распред показыв что все точки внутри сосуда явл равновероятными.2) ч-а нах-ся в однородном поле силы тяжести U(r)=mgz. Все положения при разных Z, но при одном и том же Х и Y будут равновероятны (п/э х и y м опустить)
вид распред показыв что все точки внутри сосуда явл равновероятными.2) ч-а нах-ся в однородном поле силы тяжести U(r)=mgz. Все положения при разных Z, но при одном и том же Х и Y будут равновероятны (п/э х и y м опустить) 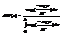 здесь h высота сосуда. Хотя поле действует, температура везде одинакова, учитывая это м получить выражение для давления. dn(z)-число частиц наход-ся в слое z,z+dz.
здесь h высота сосуда. Хотя поле действует, температура везде одинакова, учитывая это м получить выражение для давления. dn(z)-число частиц наход-ся в слое z,z+dz. 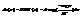
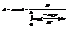
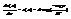 концентрация частиц на высоте z. Концентрация связана с давлением. PV=NkT - в данном случае не пригодна. P=nkT правильно, тк не б меняться с высотой и давлением р(z) и концентрацией n(z). P(z)=p(0)exp(-mgz/kT). Если отношение mgz/kT<<1, то exp(-mgz/kT)=1-mgz/kT p(z)=p(0)(1-mgz/kT) отсюда p(0)-p(z)=(mgz/kT)*p(0) получчаем изменение давления с высотой. Барометрич ф-ла исп-ся для расчета давления атмосферы на разных высотах. Строго говоря это не законно: 1) атмосфера обычно не арвновесна. 2) хим состав атмосферы на различных разный. 3) тем-ра разная на разных высотах, п/э ф-лу м исп-ть только на высотах близких к поверхности Земли.
концентрация частиц на высоте z. Концентрация связана с давлением. PV=NkT - в данном случае не пригодна. P=nkT правильно, тк не б меняться с высотой и давлением р(z) и концентрацией n(z). P(z)=p(0)exp(-mgz/kT). Если отношение mgz/kT<<1, то exp(-mgz/kT)=1-mgz/kT p(z)=p(0)(1-mgz/kT) отсюда p(0)-p(z)=(mgz/kT)*p(0) получчаем изменение давления с высотой. Барометрич ф-ла исп-ся для расчета давления атмосферы на разных высотах. Строго говоря это не законно: 1) атмосфера обычно не арвновесна. 2) хим состав атмосферы на различных разный. 3) тем-ра разная на разных высотах, п/э ф-лу м исп-ть только на высотах близких к поверхности Земли.
Выводы: давление быстро ¯ с высотой (экспоненц-но) 2) чем меньше масса молекулы, тем будет больше таких молекул в верх слоях атмосферы (азотно-кислородная атмосфера у пов-ти Земли на высоте 20 км становится почти чисто водородной 3) давление=0 только на ¥. Это означает, что отдельные молекулы м уходить от Земли как угодно далеко. Этот момент указ-т на рассеяние атмосферы.
Др объяснение рассеяния следующее: чтобы уйти от Земли дб V=11,2км/с (2 косм ск). В хвосте распред-я М всегда имеются быстрые молекулы. В то же время на больших высотах газ настолько разряжен, что длина свободного пробега сост многие тыс км, п/э ничто не мешает быстрой молекуле улететь за пределы Земли.
14. Ур-е сост-я слабонеидеаль-го газа. Сравнение теоритич ур-я сост-ия с ур-ем В-д-В.. Будем нах-ть термическое ур-е: р=р(Т,V,N). Используем: 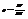 /1/, F= -
/1/, F= - 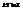 /2/. Z-статистич. сумма. Найдем lnZ=ln(kZид)=lnZид.+lnk, где Zид. – статист сумма для ид. газа, a k=
/2/. Z-статистич. сумма. Найдем lnZ=ln(kZид)=lnZид.+lnk, где Zид. – статист сумма для ид. газа, a k= 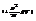 - конфигурационный интеграл.
- конфигурационный интеграл. 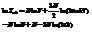 . и
. и 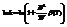 . где
. где 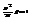 /*/ - это д.б. при b - оч. малом,
/*/ - это д.б. при b - оч. малом, 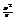 -тоже мало) т.е. мы рассматр малую область взаим-я частиц газа (при >r взаимод. мало). Если /*/ выпол-ся, тогда:
-тоже мало) т.е. мы рассматр малую область взаим-я частиц газа (при >r взаимод. мало). Если /*/ выпол-ся, тогда: 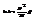 (т.к.
(т.к. 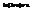 . Получаем:
. Получаем: 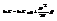 . подставим получ выраж в /2/:
. подставим получ выраж в /2/: 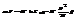 . =>
. =>
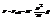 . подставим в /1/:
. подставим в /1/: 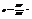
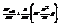
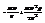 (*)- приближенное ур-е сост-я СНИ газа, где
(*)- приближенное ур-е сост-я СНИ газа, где 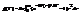 . Ур-е сост-я реаль-х газов, предлож-е В-д-В
. Ур-е сост-я реаль-х газов, предлож-е В-д-В 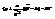 где
где 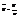 точнее опис-ет св-ва газов, чем ур-е Мен-Кл. Чтобы мож было сравнить теорит ур-е и ур-е В-д-В необходимо
точнее опис-ет св-ва газов, чем ур-е Мен-Кл. Чтобы мож было сравнить теорит ур-е и ур-е В-д-В необходимо 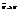 .
. 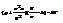 .
.
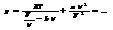 т.к.
т.к.
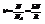 то
то 
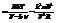 .
.
Произв nb дб << полного объема системы. (это одно из положений о слабой неидеальности) 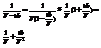 Теорит ур-е имеет след вид
Теорит ур-е имеет след вид
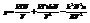 (**).
(**).
Ур-е ВдВ берется не во всей обл применимости, а только для слабонеид газа. Оба ур-я совпадут, если будет вып-ся (*)(**) след рав-ва: 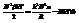 (1) данное соотношение позволяет установить точный физический смысл поправок а и b в ур-и ВДВ.
(1) данное соотношение позволяет установить точный физический смысл поправок а и b в ур-и ВДВ. 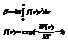 По условию слабой неидеальности
По условию слабой неидеальности  при всех к>=d в эт обл f(r)=1-(W(r)/kT)-1=-W(r)/kT. В обл с r<=d пот эн будем считать равной бесконечности. (W(r)=¥) (2 графика: кулоновское взаимод-е и со стенкой). В этом случае f(r)=-1
при всех к>=d в эт обл f(r)=1-(W(r)/kT)-1=-W(r)/kT. В обл с r<=d пот эн будем считать равной бесконечности. (W(r)=¥) (2 графика: кулоновское взаимод-е и со стенкой). В этом случае f(r)=-1 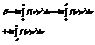 применяя ф-ю f(r) к» выражению, получим
применяя ф-ю f(r) к» выражению, получим 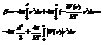 вернемся к соотношению (1)
вернемся к соотношению (1)
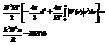
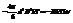
nb=(4p/6)r038N d=2r0 4/3p r03=V0 nb=4V0N
уже ранее было известно, что поправка b как-то учит-т собств V молекул. Поправка nb= учетверенному собственному V молекул
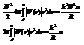
Поправка а – поправка на энергию взаим (знак – означ то, что энер взаим отриц). Связь выражается последней формулой. Оба ур-я: теорит и ВдВ-дают одинаков рез-ты для СНИ, при этом выясняется точный физ смысл пост a и b в ур-ии ВдВ. Ур-е ВдВ полуэмпирич ур-е и составл след образом: 1)берется ур-е для идеаль газа pV=RT. Идеаль газ можно сжать до точки. Реаль газ нельзя сжать до точки, т.к. есть предел связ-ый с собственн объемом молекул и обязательно > его. Значит газ мож расшир и сжимат в определ пределе. Поэтому этот объем необх вычесть из объема газа p(V-b)=RT; 2)2-ая поправка учит след обр (рис: 2-е окруж одна впис в др впис изобр шире, молек в виде точек у внутр сторон опис окруж: от одной стрелка внутрь всех окр) если молекула нах-я у стенки, то она притягив. другими молек во внутрь. Выдел-т 2-а слоя пристеноч и след за пристеноч. Притяжение обуслав дейс-ем этих 2-х слоев. Сила взимодействия б. ~ числу молекул в слоях  , точнее
, точнее
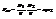 (но n1=n2)
(но n1=n2) 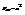 , поэтому и была внесена поправка a/V2:
, поэтому и была внесена поправка a/V2: 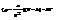 . Ур-е ВдВ простое в матем-ом отношении, учитыв глав особенн неидеаль газа: отталкив на малых расстоя-х, притяжение на >. Его конструкция такова, что оно дает верные рез-ты не только для газа: горячего и разряженного (СНИ), но и для холодного и плотного газа. Ур-е ВдВ допускает экстраполяцию на жид сост-я в-ва., но уже работает неточно. Сходство с жид-тью связано с отталкив-м мол-л на близких расст-х – с поправкой b. Физ смысл пост a и b, кот был придан при сравнении ур-ия ВдВ с теоритич ур-м, оправдан только для слабонеидеаль газа, для сильнонеид газа и жид-ти толковать так смысл поправок нельзя – это просто const-ы, чьи значения подбираются так, чтобы ур-е согласовывалось с эксперим данными.
. Ур-е ВдВ простое в матем-ом отношении, учитыв глав особенн неидеаль газа: отталкив на малых расстоя-х, притяжение на >. Его конструкция такова, что оно дает верные рез-ты не только для газа: горячего и разряженного (СНИ), но и для холодного и плотного газа. Ур-е ВдВ допускает экстраполяцию на жид сост-я в-ва., но уже работает неточно. Сходство с жид-тью связано с отталкив-м мол-л на близких расст-х – с поправкой b. Физ смысл пост a и b, кот был придан при сравнении ур-ия ВдВ с теоритич ур-м, оправдан только для слабонеидеаль газа, для сильнонеид газа и жид-ти толковать так смысл поправок нельзя – это просто const-ы, чьи значения подбираются так, чтобы ур-е согласовывалось с эксперим данными.
Ур-е ВдВ прим-ся гораздо шире, чем зона слабой неид-ти. Оно прим-ся для ид газа, слабо неид газа, неид газа, жидкости.
То сравнение, которое мы производим, б верно только в 1х2х случаях (ид газ и слабо неид газ). В 3и 4 случаях соответствия нет (неид газ и жидкость), в этой зоне поправки а и b толкуются как некоторые const, подбираемые именно на основе экспериментальных данных так, чтобы ур-е ВдВ хорошо описывало поведение вещества. Ур-е ВдВ довольно хорошо работает и в случаях 3 и 4, особенно хорошо работает для жидкостей благодаря множителю (1/ 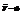 ). Этот множитель хорошо учит-т слабую сжимаемость жидкости, невозмож-ть ее сдавить до 0 в объем, меньший некоторого предельного.
). Этот множитель хорошо учит-т слабую сжимаемость жидкости, невозмож-ть ее сдавить до 0 в объем, меньший некоторого предельного.
15. Теорема о равномер-м распр-ии энергии сс. Док-во ее. Пусть сист имеет s степеней свободы => ее мех состояние опис-ся набором из 2f переменных. Есть неск-ко вариантов фор-ки. Нам удобен:Каждому квадратич-му слагаемому в среднем можно сопоставить одну и ту же эн-ю 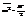 . Дело в том, что сущ масса объектов, у кот на одну степень свободы приходится как раз один квадратичный член Ei=aixi2 К/д квадратичн слагаемое м связать с энергией, прих-ся на одну степень свободы => энергия в среднем распр-ся равномерно по степеням свободы.
. Дело в том, что сущ масса объектов, у кот на одну степень свободы приходится как раз один квадратичный член Ei=aixi2 К/д квадратичн слагаемое м связать с энергией, прих-ся на одну степень свободы => энергия в среднем распр-ся равномерно по степеням свободы. 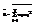
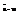 - внутр эн системы.
- внутр эн системы. 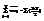
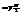
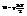 Для нахожд-я внутр эн-ии надо знать сколько квадратичных слагаемых входит в выражение эн-ии. Известно, что
Для нахожд-я внутр эн-ии надо знать сколько квадратичных слагаемых входит в выражение эн-ии. Известно, что 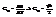 Применим эти ф-лы к 4-м случаям: 1. одноат-ый газ -
Применим эти ф-лы к 4-м случаям: 1. одноат-ый газ - 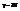 , E=Spi2/2m
, E=Spi2/2m 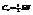 2. 2-атомн идеал газ с жесткой связью -
2. 2-атомн идеал газ с жесткой связью - 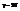 ,
, 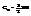 вся энергия газа: E=SEi каждой степени свободы соответсвует одно квадратичное слагаемое. 3. 2-атомн ид газ с нежесткой связью м/у молек-ми - от пред случаев молекулу отличает колеб степень мол-ы.
вся энергия газа: E=SEi каждой степени свободы соответсвует одно квадратичное слагаемое. 3. 2-атомн ид газ с нежесткой связью м/у молек-ми - от пред случаев молекулу отличает колеб степень мол-ы. 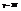 ,
, 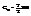 в данном случае привычная трактовка теоремы (на к/д степень свободы при-ся одна и та же энергия) не работает. Колебат степеням соот-т не один, а 2 квадратичн члена, п/э колеб степени св иногда выд-ся
в данном случае привычная трактовка теоремы (на к/д степень свободы при-ся одна и та же энергия) не работает. Колебат степеням соот-т не один, а 2 квадратичн члена, п/э колеб степени св иногда выд-ся 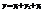
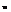 - к поступательн движ.;
- к поступательн движ.; 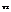 -к вращат-му;
-к вращат-му; 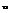 - к колебат движ. 4. кристал реш-ка - восп-ся простейшей моделью кристалла. В кристалле N атомов, к/д атом совершает колеб движ-я около положения равновесия совершенно независимо от других атомов. Положения переменных неизменны, колебания атома м разложить на 3 независ колебания, вдоль каждой из осей коор-т. Т о мы имеем для данной системы 3N колеб ст своб. При малых смещениях колебания м счит-ть гармоническими, а пот эн представленной квадратичн слагаемыми.
- к колебат движ. 4. кристал реш-ка - восп-ся простейшей моделью кристалла. В кристалле N атомов, к/д атом совершает колеб движ-я около положения равновесия совершенно независимо от других атомов. Положения переменных неизменны, колебания атома м разложить на 3 независ колебания, вдоль каждой из осей коор-т. Т о мы имеем для данной системы 3N колеб ст своб. При малых смещениях колебания м счит-ть гармоническими, а пот эн представленной квадратичн слагаемыми. 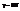 ,
, 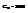 Док-во: Пусть имеется равновесн сс, имеющая тем-ру Т и эта сс такая, что эн-ю ее м. пред-ть в виде суммы квадратичных членов 1.
Док-во: Пусть имеется равновесн сс, имеющая тем-ру Т и эта сс такая, что эн-ю ее м. пред-ть в виде суммы квадратичных членов 1. 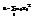 2. cc равновесна, тем-ра Т. К такой сс применимо канонич-е распред-е:
2. cc равновесна, тем-ра Т. К такой сс применимо канонич-е распред-е: 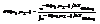 По правилу вычисл-я средних любой величины:
По правилу вычисл-я средних любой величины: 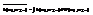
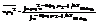 Подинтегральная ф-ия будет такая, что многократный инт-л можно разложить на произвед-е отд-х инт-ов.
Подинтегральная ф-ия будет такая, что многократный инт-л можно разложить на произвед-е отд-х инт-ов. 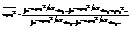 Без ущерба для точности пределы интегр-ия в каждом инт-ле м. положить равными ±¥, хотя на самом деле пределы конечны, но замена ошибки не вносит, т.к. величина
Без ущерба для точности пределы интегр-ия в каждом инт-ле м. положить равными ±¥, хотя на самом деле пределы конечны, но замена ошибки не вносит, т.к. величина  -энергия, связан-я с какой-то степенью свободы, ее max это энергия всей сс вместе взятой, она равна
-энергия, связан-я с какой-то степенью свободы, ее max это энергия всей сс вместе взятой, она равна 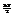 , тогда кажд сомножитель м. вычислить независимо, тогда инт-лы почти все сократятся и ост-ся:
, тогда кажд сомножитель м. вычислить независимо, тогда инт-лы почти все сократятся и ост-ся: 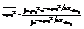 Из мат-ки:
Из мат-ки: 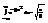
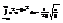
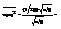
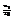 ,где
,где 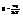 =>
=> 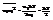 . Некот физ сист, где энерг м/б представлена в виде суммы квадратич-х слагаем-х. 1) 1-атомный идеаль газ: энерг сист
. Некот физ сист, где энерг м/б представлена в виде суммы квадратич-х слагаем-х. 1) 1-атомный идеаль газ: энерг сист 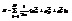 , пременные рхi, pyi, pzi – всего 3N. Тогда теорема запишется след образом
, пременные рхi, pyi, pzi – всего 3N. Тогда теорема запишется след образом 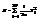 , т.е. теорема о равномерном распределении энерг по степеням свободы применима.
, т.е. теорема о равномерном распределении энерг по степеням свободы применима.
17. Распред-е Ферми-Дирака и Бозе-Энштейна. Прямое примен-е канонич распред-я (КР) невоз-но, т.к. в нем нет учета тождест-ти частиц и пр-па Паули. В кач-ве квазинезависим. подсист. берется совок-ть час-ц, находящихся в одном квантов состоянии. Все другие час-цы образ-т по отнош-ию к выделенным термостат. Число частиц в выделенном квантов сос-ии меняется, поэтому эта система с перемен-м числом час-ц, поэтому для ее исслед-я н. прим-ть БКР. a -квантов сост-ие; na- число частиц в a -ом сос-ии. Т.к част взаим-т, то a постоянно мен-ся. Но совок-ть 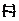 будет постоян-м.
будет постоян-м. 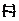 - число час-ц в сос-ии a. Чтобы найти
- число час-ц в сос-ии a. Чтобы найти 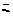 в кач-ве подсист н. использ-ть сов-ть всех частиц в a-ом сос-ии. Все др част газа образ-т по отнош-ю к этим термостат. Поэтому применим к ним БКР:
в кач-ве подсист н. использ-ть сов-ть всех частиц в a-ом сос-ии. Все др част газа образ-т по отнош-ю к этим термостат. Поэтому применим к ним БКР: 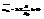
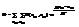 - больш стат сумма. ea -эн-я час-ц в a- ом сост-ии(всех час-ц). W -число различных сос-ий сист при заданной эн-ии и задан-ом числе част. m -химич пот-л. Все частицы в одном квант сос-ии имеют одну и ту же эн-ию. Эн-я сист в целом
- больш стат сумма. ea -эн-я час-ц в a- ом сост-ии(всех час-ц). W -число различных сос-ий сист при заданной эн-ии и задан-ом числе част. m -химич пот-л. Все частицы в одном квант сос-ии имеют одну и ту же эн-ию. Эн-я сист в целом 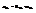 Т.о. эн-я сист однозначно опред-ся числом э-ов.
Т.о. эн-я сист однозначно опред-ся числом э-ов. 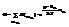 Утверждаем, что
Утверждаем, что 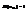 Это рав-во обеспеч-ся тем, что все э-ны принцип-но не различимы. Поэтому сос-ия подсист различ-ся только по числу частиц в ней.
Это рав-во обеспеч-ся тем, что все э-ны принцип-но не различимы. Поэтому сос-ия подсист различ-ся только по числу частиц в ней. 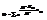 1) Фермионы (одинаковые част с полуцелым спином: е, р...). na=0 или na=1.
1) Фермионы (одинаковые част с полуцелым спином: е, р...). na=0 или na=1. 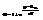
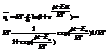 =>
=> 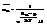 (это и есть Ферми-Дирака) 2) бозоны – част с 0 или целым спином. na= 0,1...N, т.к число част велико, то N=¥.
(это и есть Ферми-Дирака) 2) бозоны – част с 0 или целым спином. na= 0,1...N, т.к число част велико, то N=¥. 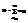 Эта сумма сход-ся, если
Эта сумма сход-ся, если 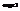 при любом Е, для этого должно
при любом Е, для этого должно 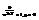 . Тогда:
. Тогда:  убывающая прогрессия
убывающая прогрессия 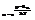
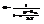
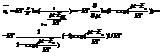 =>
=> 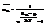 -распред-е Бозе-Эйнштейна.
-распред-е Бозе-Эйнштейна.
Распр-ие част в квант ид газах по энергиям. Найти dn(e), e,e+de. 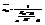 число ч-ц опр-ся только энергией состояний. Как правило эн ч-ц квазидискретна, т.е. уровни эн идут настолько густо, что энергию м считать непрерывной величиной. С одной стороны de так велик, что на этот интер-л прих-ся большое кол-во dW. С др стороны этот интер-л так мал, что в его пределах
число ч-ц опр-ся только энергией состояний. Как правило эн ч-ц квазидискретна, т.е. уровни эн идут настолько густо, что энергию м считать непрерывной величиной. С одной стороны de так велик, что на этот интер-л прих-ся большое кол-во dW. С др стороны этот интер-л так мал, что в его пределах 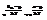 Тогда
Тогда 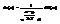 Для одной частицы:
Для одной частицы: 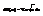
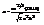 (2S+1) –учит-т разные спины.
(2S+1) –учит-т разные спины. 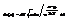
18. Распределение Больцмана и критерии вырождения газа. Распредел-ие час-ц в квант-х ид. газах по энергии. Найдем число час-ц dn(e) в интервале от e до e+de Исполь-ем фор-лу 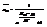 Б. предполагать, что с 1 стороны интервал de настолько велик, что на него приход-ся большое кол-во квант. сост-ний dW(e). С др. стороны этот инт-ал настолько мал, что в его пределах
Б. предполагать, что с 1 стороны интервал de настолько велик, что на него приход-ся большое кол-во квант. сост-ний dW(e). С др. стороны этот инт-ал настолько мал, что в его пределах 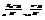 Þ
Þ 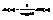 Число кван-ых сост-ий dW(e) для первой час-цы
Число кван-ых сост-ий dW(e) для первой час-цы 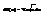 а
а 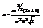 (2s+1) учитывает разные спин-е сост-я объекта. Окончательно
(2s+1) учитывает разные спин-е сост-я объекта. Окончательно 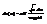 В такой форме распр-ие прим-ся на практике. Распределение Больцмана и критерии вырождения газа. Допустим энергия изм-ся от 0 до ¥ Но такого не м. б. т. к. 0-ой энер-ии не м. б. Предположим, что выполн-ся условие
В такой форме распр-ие прим-ся на практике. Распределение Больцмана и критерии вырождения газа. Допустим энергия изм-ся от 0 до ¥ Но такого не м. б. т. к. 0-ой энер-ии не м. б. Предположим, что выполн-ся условие 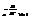 (*);
(*);
тогда 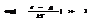 для этого случая распределение Ферми- дирака упрощается
для этого случая распределение Ферми- дирака упрощается 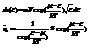
Т. о. Можно упростить форм-лу
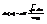 след-но
след-но
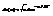 (**)(распределение Максвелла для эне ч-ц) она была выведена в рамках классической физики,=> ясно, что критерий (*) опр-т воз-ть применения классич физике. При выполнении (*) мы получанм (**), кот наз распределением Больцмана для квантого идеального газа. Она часто применяется в разных расчетах, когда с одной стороны уже пригодна классич физика, а с др стороны нам нужно подчеркнуть, что система квантовая с дискретными уровнями энергии. Заметим, что когда отброшена 1, то полностью теряется различие м/у бозонами и фермионами. Критерий (*) хорош, но очень глух и прозрачен.
(**)(распределение Максвелла для эне ч-ц) она была выведена в рамках классической физики,=> ясно, что критерий (*) опр-т воз-ть применения классич физике. При выполнении (*) мы получанм (**), кот наз распределением Больцмана для квантого идеального газа. Она часто применяется в разных расчетах, когда с одной стороны уже пригодна классич физика, а с др стороны нам нужно подчеркнуть, что система квантовая с дискретными уровнями энергии. Заметим, что когда отброшена 1, то полностью теряется различие м/у бозонами и фермионами. Критерий (*) хорош, но очень глух и прозрачен. 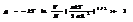
подставим в (*) 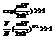
Когда это рав-во вып-ся то примен-ма класс-ая физ-ка и все зак-ны выполн-ся. Если оно не выпол-ся, то класс-ка не применима. Тогда надо польз-ся распред-ем Бозе-Эйнш-Дирака. При этом нельзя применять и др. класс-ие законы. Если вып-ся нер-во (…)<1, то о применении классики не м б и речи, даже для оценок, для эт ввден спец термин - вырождение газа. Газ вырождается-это и есть отступ-ие газа от св-в класс-го ид. газа, связанное с квант-ми особен-ми повед-ия час-ц. Например ур-ие Менд-Клап pV=uRT не будет справ-во для выврожд-го газа Причин же больше: есть силовое вз-вие т. е. не связано с кван-ми особ-ми. Выполнению неравен-ва способст-ет:1)большая масса m; 2)высокая тем-ра Т; 3)большой удельный обьем 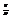 или малая плот-ть. Низкая плотность=> большое расстояние м/у ч-ми=> не н учит-ть обменный эффект. Свободное движение по квантовой теории имеет некот стороны, некот черты такие же как у классич ч-ц (нерпер эн и импульс e=p2/2m, такая же как в классике связь м/у эн и импульсом) В класс-ке не учит-ся ферм. и бозоны. т. к. если критерий вырож-н то число возм-ных кван-ых сост-ний для 1 час-цы на много превыш-ет число час-ц. След-но кв-ых сост-ний много а час-ц мало. Тогда в больш-ве сост-ний нет час-ц и лишь в нек-ых имее-ся по 1 час-це в этом случ-е ни тожд-ть ни запрет Паули никак себя проявить не могут. Можно оцен-ть когда мож-о применять класс-ую физ-у и когда ее примн-ие дает незнач-ую ошибку. Ясно что если мы буд-м из-т вопр-сы в тех случ-х когда это нер-во невыпол-ся мы получим резко отл-ся формы повед-ия газа от станд-ых.
или малая плот-ть. Низкая плотность=> большое расстояние м/у ч-ми=> не н учит-ть обменный эффект. Свободное движение по квантовой теории имеет некот стороны, некот черты такие же как у классич ч-ц (нерпер эн и импульс e=p2/2m, такая же как в классике связь м/у эн и импульсом) В класс-ке не учит-ся ферм. и бозоны. т. к. если критерий вырож-н то число возм-ных кван-ых сост-ний для 1 час-цы на много превыш-ет число час-ц. След-но кв-ых сост-ний много а час-ц мало. Тогда в больш-ве сост-ний нет час-ц и лишь в нек-ых имее-ся по 1 час-це в этом случ-е ни тожд-ть ни запрет Паули никак себя проявить не могут. Можно оцен-ть когда мож-о применять класс-ую физ-у и когда ее примн-ие дает незнач-ую ошибку. Ясно что если мы буд-м из-т вопр-сы в тех случ-х когда это нер-во невыпол-ся мы получим резко отл-ся формы повед-ия газа от станд-ых.
19. Вырожденный фермион. газ. Электроны в металлах. Мы б. производить изуч-е на основе формул: (1) 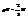 ; (2)
; (2) 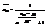 ; (3)
; (3) 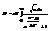 ; (4)
; (4) 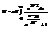 ; Фермионы не м. скаплив-ся ни в каком сост-ии, это им запрещает при-п Паули.=> ф-ла (3) для ферм-ов дает фактически полное число ч-ц. Рассмотрим изменение химич. потенц-л m. (График: ось ординат-m,ось абсцисс- Т, линия от знач-я m до Т0 идёт по прямой, затем плавно переходит в параб. опускающ-ся ниже оси Т.) При уменьш. Т хим. потенц-л должен увелич-ся. При высоких Т, как для всех классич-х систем он отриц-лен. => При уменьш. Т, хим. потенц-л увелич-ся. Можно доказать, что монотонно: mmax = m (0), при Т=0. Здесь нет запрета на m > 0. Выделим область темп-р, в пределах кот-й м. б. m » m(0) или =m0. Это м. б. в каком-то инт-ле темп-р от 0 до Т0 (0£Т£Т0). В определ-х случаях этот интер-л м. составлять 10 тыс.Т0. Обратимся к распредел-ю Ферми:
; Фермионы не м. скаплив-ся ни в каком сост-ии, это им запрещает при-п Паули.=> ф-ла (3) для ферм-ов дает фактически полное число ч-ц. Рассмотрим изменение химич. потенц-л m. (График: ось ординат-m,ось абсцисс- Т, линия от знач-я m до Т0 идёт по прямой, затем плавно переходит в параб. опускающ-ся ниже оси Т.) При уменьш. Т хим. потенц-л должен увелич-ся. При высоких Т, как для всех классич-х систем он отриц-лен. => При уменьш. Т, хим. потенц-л увелич-ся. Можно доказать, что монотонно: mmax = m (0), при Т=0. Здесь нет запрета на m > 0. Выделим область темп-р, в пределах кот-й м. б. m » m(0) или =m0. Это м. б. в каком-то инт-ле темп-р от 0 до Т0 (0£Т£Т0). В определ-х случаях этот интер-л м. составлять 10 тыс.Т0. Обратимся к распредел-ю Ферми: 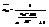 если
если 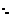 >
> 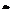 , при Т® 0,
, при Т® 0,  ® 0. Если
® 0. Если 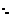 <
< 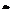 , при Тà 0,
, при Тà 0,  ® 1. Вблизи абс. 0 фермионы заполняют все квант-е сост-я, чья энергия ниже
® 1. Вблизи абс. 0 фермионы заполняют все квант-е сост-я, чья энергия ниже 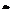 Т.о. энергия eF=mо, отделяет заполненное состояние от незаполненных. Обознач-е eF- энергия Ферми. (Графики:1-й ось орд-т -
Т.о. энергия eF=mо, отделяет заполненное состояние от незаполненных. Обознач-е eF- энергия Ферми. (Графики:1-й ось орд-т -  , ось абсц-с -e, график- прямая от e=0,n=1 до eF, n=1, затем ступенькой к оси e дальше -по оси. [при Т=0]. 2-й -тот же, но в области eF спуск плавный [при 0£Т£ТО). Ч-ы имеющие энергию ниже энергии Ферми, в тепловых и многих других процессах не участвуют. В следствие запрета Паули эл-ы с эн ниже эн Ферми не м изменять свою энергию и даже свое квантовое состояние. Имеется зона, где эл-ы легко меняют свое квант сост-е и уровни эн-и, эта зона располагается вблизи эн Ферми, она соост-т актив эл-м. Ниже располаг-ся пассивн зона. Теплоемкость эл газа в металле =0, т к в тепловом явлении уч-т ничтожная часть эл-в. будем считать, что газ сильно вырожден.,(*)
, ось абсц-с -e, график- прямая от e=0,n=1 до eF, n=1, затем ступенькой к оси e дальше -по оси. [при Т=0]. 2-й -тот же, но в области eF спуск плавный [при 0£Т£ТО). Ч-ы имеющие энергию ниже энергии Ферми, в тепловых и многих других процессах не участвуют. В следствие запрета Паули эл-ы с эн ниже эн Ферми не м изменять свою энергию и даже свое квантовое состояние. Имеется зона, где эл-ы легко меняют свое квант сост-е и уровни эн-и, эта зона располагается вблизи эн Ферми, она соост-т актив эл-м. Ниже располаг-ся пассивн зона. Теплоемкость эл газа в металле =0, т к в тепловом явлении уч-т ничтожная часть эл-в. будем считать, что газ сильно вырожден.,(*) 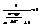 при e < eF,
при e < eF, 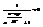 при e > eF
при e > eF
Воспольз-ся ф-лой (3). 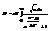 »
»  =
= 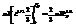 , Þ
, Þ 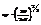 ,
, 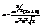 подставим а в фор-лу для EF (**)
подставим а в фор-лу для EF (**) 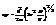 Энергия Ферми eF »1-10 эВ зависит от сорта(массы) и концентрации ч-ц. Рссмотрим зависим-ть p от T и V, и e от T и V.
Энергия Ферми eF »1-10 эВ зависит от сорта(массы) и концентрации ч-ц. Рссмотрим зависим-ть p от T и V, и e от T и V. 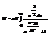 При достаточно низких Т интеграл упрощается, используя ф-лу (*) Þ
При достаточно низких Т интеграл упрощается, используя ф-лу (*) Þ 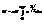 ,
,  , eF ~
, eF ~ 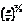 , U~
, U~ 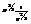 . Энергия фермионного газа практич. не зависит от темпер-ры и концентрации ч-ц Þ теплоёмкость СV=
. Энергия фермионного газа практич. не зависит от темпер-ры и концентрации ч-ц Þ теплоёмкость СV= 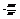 фермион. газа =0. PV=2/3U~V2/3 p~1/V5/3
фермион. газа =0. PV=2/3U~V2/3 p~1/V5/3