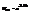Формула Эйнштейна для вероятности флуктуации. Ограничения на точность измерений, связанные с наличием флуктуаций.

=> .Всякая флуктуация связана с изменением энтропии в системе. Пусть x – один или несколько параметров, которые изменяются при флуктуации. Вероятность что x попадет в [ x, x +d x ] 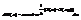, где 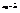- равновесное значение величины. Значит нужно рассчитать изменение S, при изменении x от x ₀ до x. Возьмем точку а и допустим, что произошла флуктуация и пр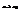и и 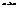. При флукт. в равновесной изолир. системе энергия не изменяется. При флуктуац. мы отходим от рвановес, т.е. энтропия может только уменьшаться. Выделим состояние b. S_b = S_c. Но для b x=x₀, для c x. Переход b в c есть равновесный адиабат. переход, при котором просходит такое измен. x, которое возникло в рез-те флуктуации. В нем 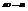. Можно связать DU с DS. 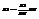. Т.к. 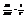то 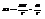. Далее 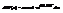- формула Эйнштейна. Вероятность флуктуации опред. работой равновесного адиабат. процесса при котором имеет место такое же изменение параметра x, которое возникло в рез-те флуктуации. Точность. Возьмем динамометр. Пусть d-отрезок порядка 0,1 цены деления. k – жесткость. 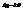- оценка min груза, который можно измерить. Значит для повыш. точности нужно брать не жесткую пружину, но на слабой пружине заметны флуктуации длины пружины. Пусть 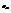- ср. квадратичн. флукт. длины. Если 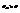, то мы не сможем отличить смещение стрелки под действ. легкого груза от спонтанного смещ. в рез-те флукт. Вер-ть того, что длина пружины x будет 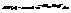, где 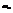- работа адиабатич. растяж. пружины на отрезок 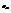. Работа растяжения .

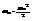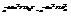, т.е. 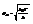, k ₀ – пост. Больцмана. Прямой способ повышения точности – охлаждение прибора. Если флуктуация достигает порядка деления шкалы, то заметить смещение в ре-те флукт. легко. XIX-XX веках флукт. очень была важна.

25. Броуновское движение. Вывод формулы Эйнштейна-Смолуховского. Связь броуновского движения с диффузией и другими явлениями. БД – беспоряд. движение малых частиц в среде жидк. или газа. Оно резко противоречило II закону ТД, т.к. в рез-те вязкого трения должно было остановиться. Но оно бесконечно. Только теория флукт. объяснила БД. Но танец пылинок в солн. лучах – это не БД, это родственное, т.к. вызвано конвект. потоками. Истинное БД наблюд. и при отключении конвекции. Одна молекула не может сдвинуть пылинку как комар не сдвинет паровоз. Движение объясняется флукт. давления по разные стороны от пылинок. С одного бока меняется по разному, чем от другого. Но это очень похоже на БД. Вывод. На движ. частицу 2 силы: 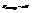, где 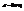, r – радиус, h - коэфф. вязкого трения. Также F – сила в рез-те флукт. давления по обе стороны от шарика. Величина и напр. F хаотич. меняется с теч. времени, не знаем F (t). Смещение частицы 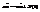, где X(t) – проекц. случ. силы. Проинтегр. невозможно, получим средние. Пусть в поле зрения N>>1 частиц. Случ. сумму X(t) можно исключить. Выходим на среднеквадр. величины. 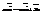- усредняем. 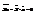. 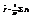, , 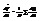т.е. 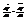- и для 2 пр-ных также. 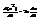, 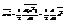. Дифф. еще раз 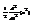, или

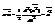. Получим

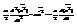. Степени своб. частицы попадают под действие теор. о равном. распредел. энергии. 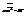. Обозначим 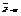, , 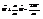пусть 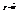. Общее решение ур-я будет 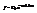. Частное решение положим 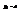, 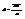. Окончательно 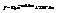. Проинтегрировав, получим 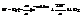, где C₂=0, положив начало движ. отн. точки отсчета. Первое слагаемое не дает ощутимый вклад, поэтому 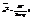- ф-ла Эйнштейна-Смолуховского. Обсуждение. Допускает простую эксп. проверку. Т.е. измеряем x в поле зрения. Знаем T, r, h. Опыты подтвердили закон. Для проверки достаточно наблюдать одну частицу. И вид такой – зигзаги всякие. Также если в нач. момент молекулы были в одном пр-ве, открываем перегородку, найдем время возвращения в первонач. объем. Это время резко возрастает с кол-вом числа частиц. Если рассм. явл. убыли броун. частиц в пределах нач. круга – диффузия. Сущ. связь коэфф. диффузии с коэфф. вязкости. Есть также распред. броун. частиц в поле силы тяжести по высоте. Потоки вверх и вниз уравновешивают друг друга.

1.Идеальный газ в МКТ. Вывод распределения Максвелла.

2.Вычисл. давл-ия на стенку сосуда.

3. Квазинезависимые подсистемы.

4. Макр-ое сост. с-мы

5. Определение энтропии и ее свойства. Закон возрастания энтропии в замкнутой системе.

6. Связь энтропии с числом микросост. в локально-равновесных системах. Принцип Больцмана и ф-ла Больцмана. Статист. толкование закона созраст. энтропии. Пример примен. метода Больцмана.

7. Равновесный процесс. Статистическое определ. T, хим.потенц, p. Основное ТД р-во-н-во. Статфизика и ТД.

8. Вывод формулы канонического распределения.

9. Особенности и св-ва канонического распределения. Вычисление ТД величин с помощью КР.

10. Приближенное выражение для статистической суммы. Приближенное выражение для числа квантовых состояний. Классическое каноническое распределение.

11. Расчет статистической суммы для классического одноатомного идеального газа. Нахождение ТД ф-ций и ТД ур-я состояния системы

12. Распределение Максвелла-Больцмана. Распределение Максвелла и его свойства. Распределение для модуля скорости и энергии частицы. Распределение Больцмана. Барометрическая ф-ла.

13. Реальные газы. Модель слабонеидеального газа. Вычисление конфигурационного интеграла.

14. Ур-е сост-я слабонеидеаль-го газа. Сравнение теоритич ур-я сост-ия с ур-ем В-д-В..

15. Теорема о равномер-м распр-ии энергии сс. Док-во ее.

16. Классич-я теория теплоемкости. Затрудн-я этой теории. Простейш-я квантовая теория теплоемкости твердого тела. Теплоемк-ть газов в свете квантовых представлений.

17. Распред-е Ферми-Дирака и Бозе-Энштейна.

18. Распределение Больцмана и критерии вырождения газа. Распредел-ие час-ц в квант-х ид. газах по энергии.

19. Вырожденный фермион. газ. Электроны в металлах.

20. ЭМ излучения как фотонный газ. Формула Планка.

21. Законы равновесного ЭМ излучения. Излучение АЧТ. Уравнение состояния фотонного газа. Функция Стефана-Больцмана для интегральной плотности энергии.

22. Флуктуации термодинамических величин. Расчет флуктуаций энергии с помощью канонического распределения.

23. Формула Эйнштейна для вероятности флуктуации. Ограничения на точность измерений, связанные с наличием флуктуаций.

24. Флуктуация объема. Флуктуация плотности. Молекулярное рассеяние света.

25. Броуновское движение. Вывод формулы Эйнштейна-Смолуховского. Связь броуновского движения диффузией и другими явлениями.