Задание
Провести статистическую обработку выборочных данных о пробеге
автомобилей до снятия с эксплуатации. Данные о пробеге автомобилей
приведены в таблице исходных данных.
Таблица исходных данных. Пробег автомобилей до снятия с эксплуатации (тыс. км.)
| № авт. | Пробег | № авт. | Пробег | № авт. | Пробег | № авт. | Пробег | № авт. | Пробег | № авт. | Пробег |
Определение числовых характеристик.
| Обзначение | Наименование показателя | Значение, тыс. км. |
| t | Среднее | 558,4 |
| mt | Стандартная ошибка | 1,881085343 |
| Me | Медиана | |
| Mo | Мода | |
| S | Стандартное отклонение | 19,72898952 |
| D | Дисперсия выборки | 389,2330275 |
| E | Эксцесс | -0,376237187 |
| A | Асимметричность | -0,158029859 |
| R | Интервал | |
| t min | Минимум | |
| t max | Максимум | |
| Сумма | ||
| n | Счет | |
| Vt | Коэффициент вариации | 0,42 |
2.1. Определяют коэффициент вариации:
2.2. Определяют размах варьирования показателя:
R= 604 – 512 = 92 тыс. км
2.3. Рассчитывают количество интервалов:
k = 
= 10,48
Полученное значение округляют до целого числа, k=10
2.4. Определяют величину одного интервала:
h = 
= 9,2 h=9
2.5. Определяют границы интервалов.
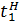= 512 – 0,5x9 = 507,5
Верхняя граница первого интервала и его середина равны:
= 507,5 + 9 = 516,5 
= 507,5+0,5x9 = 511,5
2.6 Определяют абсолютные частоты попадания значений показателя в каждый интервал путём подсчёта числа значений, попадающих в соответствующие интервалы. Подсчёт числа попаданий значений в интервал производится в соответствии с формулой:
2.7. Определяют вероятность попадания показателя в каждый интервал. Например, для первого интервала:
= 
= 
= 0,018018
Затем определяют накопленную частоту суммированием абсолютной частоты в интервале и абсолютных частот предыдущих интервалов. Результаты выполнения операции заносим в таблицу. Для последнего интервала накопленная частота должна быть равна объёму выборки.
| № интер вала | Границы интервалов | Часто- та | Накоплен- ная частота | Относи- тельная частота | Накоплен- ная отн. частота | ||
| нижняя | Верхняя | середи на | |||||
| 507,5 | 516,5 | 511,5 | 0,018018 | 0,018018 | |||
| 516,5 | 525,5 | 520,5 | 0,063063 | 0,081081 | |||
| 525,5 | 534,5 | 529,5 | 0,045045 | 0,126126 | |||
| 534,5 | 543,5 | 538,5 | 0,072072 | 0,198198 | |||
| 543,5 | 552,5 | 547,5 | 0,18018 | 0,378378 | |||
| 552,5 | 561,5 | 556,5 | 0,171171 | 0,549549 | |||
| 561,5 | 570,5 | 565,5 | 0,18018 | 0,729729 | |||
| 570,5 | 579,5 | 574,5 | 0,108108 | 0,837837 | |||
| 579,5 | 588,5 | 584,5 | 0,108108 | 0,945945 | |||
| 588,5 | 597,5 | 592,5 | 0,027027 | 0,972972 | |||
| 597,5 | 606,5 | 602,5 | 0,018018 | 0,853152 |
2.8. Строят таблицу частот по следующей форме
Графическое представление выборочных функций.
По данным таблицы частот строят гистограмму:
Строят график полигона распределения пробега автомобилей:
Построение функции распределения
Для построения эмпирической функции распределения небходимо создать исходную таблицу (таблица 6). В первом столбце указываются границы интервалов, а во втором соответствующие им накопленные вероятности. Исходная таблица данных отличается от таблицы частот тем, что границы интервалов повторяются, так как значение верхней границы интервала равно значению нижней границы следующего интервала.
| Границы интервалов | Накопленная вероятность |
| 516,5 | |
| 525,5 | |
| 525,5 | |
| 534,5 | |
| 534,5 | |
| 543,5 | |
| 543,5 | |
| 552,5 | |
| 552,5 | |
| 561,5 | |
| 561,5 | |
| 570,5 | |
| 570,5 | |
| 579,5 | |
| 579,5 | |
| 588,5 | |
| 588,5 | |
| 597,5 | |
| 597,5 | |
| 606,5 | |
| 606,5 | |
| 615,5 |
График эмпирической функции распределения
пробега
автомобилей до снятия с эксплуатации.
Таблица 6.
5. Вывод:
По данным гистограммы и графику полигона распределения пробега автомобилей можно сделать вывод, что наибольшая частота наблюдаеться у автомобилей с пробегом 547,5 и 565,5 тыс. км. Это сведетельствует о том, что автомобили с пробегом в этих числовых значениях чаще всего, а именно 20 из 25 автомобилей, подлежат снятию с эксплуатации. Наименьшее число автомобилей, подлежащих снятию с эксплуатации наблюдаеться с пробегом 610,5 тыс. км. – 1 автомобиль из 25.
По графику эмпирической функции распределения пробега можно сделать вывод:
Вероятность снятия с эксплуатации автомобилей с пробегом до 520 тыс. км будет минимальной: 1,8 % (2 автомобиля из 111)
С пробегом более 605 тыс. км будет максимальной: 99% (110 автомобилей из 111)