Элементарные функции и их свойства
Постоянная функция.
Постоянная функция задается на множестве всех действительных чисел формулой 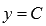 , где C – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой.
, где C – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой.
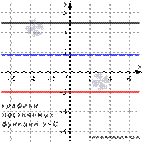
Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку с координатами (0,C). Для примера покажем графики постоянных функций y=5, y=-2 и  , которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.
, которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.
Свойства постоянной функции.
· Область определения: все множество действительных чисел.
· Постоянная функция является четной.
· Область значений: множество, состоящее из единственного числа С.
· Постоянная функция невозрастающая и неубывающая (на то она и постоянная).
· Говорить о выпуклости и вогнутости постоянной не имеет смысла.
· Асимптот нет.
· Функция проходит через точку (0,C) координатной плоскости.
Корень n -ой степени.
Рассмотрим основную элементарную функцию, которая задается формулой 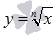 , где n – натуральное число, большее единицы.
, где n – натуральное число, большее единицы.
Корень n -ой степени, n - четное число.
Начнем с функции корень n -ой степени при четных значениях показателя корня n.
Для примера приведем рисунок с изображениями графиков функций  и
и  , им соответствуют черная, красная и синяя линии.
, им соответствуют черная, красная и синяя линии.
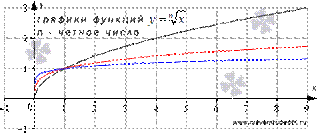
Аналогичный вид имеют графики функций корень четной степени при других значениях показателя.
Свойства функции корень n -ой степени при четных n.
· Область определения: множество всех неотрицательных действительных чисел  .
.
· При x=0 функция 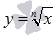 принимает значение, равное нулю.
принимает значение, равное нулю.
· Эта функция общего вида (не является четной или нечетной).
· Область значений функции:  .
.
· Функция 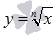 при четных показателях корня возрастает на всей области определения.
при четных показателях корня возрастает на всей области определения.
· Эта функция имеет выпуклость, направленную вверх, на всей области определения, точек перегиба нет.
· Асимптот нет.
· График функции корень n -ой степени при четных n проходит через точки (0,0) и (1,1).
К началу страницы
· Корень n -ой степени, n - нечетное число.
Функция корень n -ой степени с нечетным показателем корня n определена на всем множестве действительных чисел. Для примера приведем графики функций  и
и  , им соответствуют черная, красная и синяя кривые.
, им соответствуют черная, красная и синяя кривые.

При других нечетных значениях показателя корня графики функции 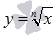 будут иметь схожий вид.
будут иметь схожий вид.
Свойства функции корень n -ой степени при нечетных n.
· Область определения: множество всех действительных чисел.
· Эта функция нечетная.
· Область значений функции: множество всех действительных чисел.
· Функция 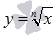 при нечетных показателях корня возрастает на всей области определения.
при нечетных показателях корня возрастает на всей области определения.
· Эта функция вогнутая на промежутке  и выпуклая на промежутке
и выпуклая на промежутке  , точка с координатами (0,0) – точка перегиба.
, точка с координатами (0,0) – точка перегиба.
· Асимптот нет.
· График функции корень n -ой степени при нечетных n проходит через точки (-1,-1), (0,0) и (1,1).
К началу страницы
Степенная функция.
Степенная функция задается формулой вида 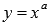 .
.
Рассмотрим вид графиков степенной функции и свойства степенной функции в зависимости от значения показателя степени.
Начнем со степенной функции с целым показателем a. В этом случае вид графиков степенных функций и свойства функций зависят от четности или нечетности показателя степени, а также от его знака. Поэтому сначала рассмотрим степенные функции 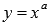 при нечетных положительных значениях показателя a, далее - при четных положительных, далее - при нечетных отрицательных показателях степени, и, наконец, при четных отрицательных a.
при нечетных положительных значениях показателя a, далее - при четных положительных, далее - при нечетных отрицательных показателях степени, и, наконец, при четных отрицательных a.
Свойства степенных функций с дробными и иррациональными показателями (как и вид графиков таких степенных функций) зависят от значения показателя a. Их будем рассматривать, во-первых, при a от нуля до единицы, во-вторых, при a больших единицы, в-третьих, при a от минус единицы до нуля, в-четвертых, при a меньших минус единицы.
В заключении этого пункта для полноты картины опишем степенную функцию с нулевым показателем.
Степенная функция с нечетным положительным показателем.
Рассмотрим степенную функцию 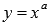 при нечетном положительном показателе степени, то есть, при а=1,3,5,….
при нечетном положительном показателе степени, то есть, при а=1,3,5,….
На рисунке ниже приведены графики степенных фнукций 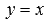 – черная линия,
– черная линия,  – синяя линия,
– синяя линия, 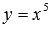 – красная линия,
– красная линия,  – зеленая линия. При а=1 имеем линейную функцию y=x.
– зеленая линия. При а=1 имеем линейную функцию y=x.
