сверхразрешимый группа лемма
Определение 2.1. Группа называется сверхразрешимой, если она обладает нормальным рядом с циклическими факторами.
Лемма 2.1 [1, Лемма 26.1].
(1) Каждая подгруппа и каждая фактор-группа сверхразрешимой группы сверхразрешимы.
(2) Прямое произведение сверхразрешимых групп является сверхразрешимой группой.
(3) Сверхразрешимая группа разрешима.
Доказательство:
(1) Пусть группа G сверхразрешима. Тогда группа G обладает нормальным рядом с циклическими факторами:
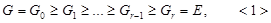
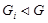 и фактор-группы
и фактор-группы  циклические для всех i. Пусть
циклические для всех i. Пусть  и
и  Тогда подгруппа U имеет ряд
Тогда подгруппа U имеет ряд

причём 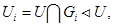 для вех i. Далее
для вех i. Далее
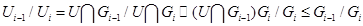
и фактор-группа 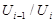 циклическая. Итак, ряд <2> нормальный и его факторы циклические. Поэтому подгруппа U сверхразрешима.
циклическая. Итак, ряд <2> нормальный и его факторы циклические. Поэтому подгруппа U сверхразрешима.
Пусть  . Рассмотрим ряд
. Рассмотрим ряд
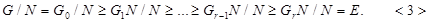
Ясно, что 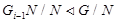 для всех
для всех  , поэтому ряд <3> нормальный.
, поэтому ряд <3> нормальный.
Далее,
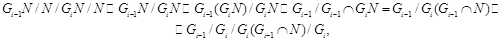
поэтому факторы ряда <3> циклические и фактор-группа  сверхразрешима.
сверхразрешима.
(2) Пусть G и H - сверхразрешимые группы. Тогда группы G и H обладают нормальными рядам
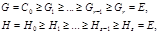
с циклическими факторами 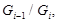
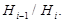 Рассмотрим прямое произведение
Рассмотрим прямое произведение 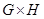 и построим ряд
и построим ряд
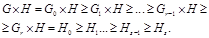
Этот ряд нормальный и его факторы циклические.
(3) Пусть группа 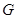 сверхразрешима. Тогда группа
сверхразрешима. Тогда группа 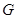 обладает нормальным рядом <1> с циклическими факторами. Так как
обладает нормальным рядом <1> с циклическими факторами. Так как 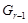 циклическая, то
циклическая, то 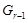 разрешима. Так как
разрешима. Так как 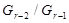 и
и 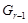 циклические, то они разрешимы, поэтому
циклические, то они разрешимы, поэтому 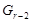 разрешима по лемме 1.2. Теперь
разрешима по лемме 1.2. Теперь 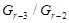 и
и 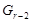 разрешимы, значит и
разрешимы, значит и 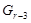 разрешима по лемме 1.2, и т.д. Через конечное число шагов получаем, что группа
разрешима по лемме 1.2, и т.д. Через конечное число шагов получаем, что группа 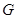 разрешима.
разрешима. 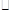
Лемма 2.2 [1, Лемма 26.2]. (1) Если группа G содержит нормальную циклическую подгруппу K и фактор-группа G/K сверхразрешима, то группа G сверхразрешима.
(2) Если фактор-группа G/Z(G) сверхразрешима, то группа G сверхразрешима.
(3) Нильпотентная группа сверхразрешима.
Доказательство.
(1) Так как G/Kсверхразрешима, то имеется нормальный ряд
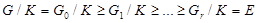
с циклическими факторами 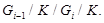 Рассмотрим ряд
Рассмотрим ряд
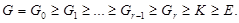 <4>
<4>
Так как 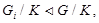 то
то  и ряд <4> нормальный.
и ряд <4> нормальный.
Кроме того, факторы  циклические для
циклические для 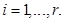 Далее,
Далее,  - циклическая группа. Значит ряд <4> нормальный с циклическими факторами и группа
- циклическая группа. Значит ряд <4> нормальный с циклическими факторами и группа 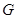 сверхразрешима.
сверхразрешима.
(2) Пусть 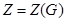 . Так как
. Так как 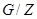 сверхразрешима, то имеется нормальный ряд
сверхразрешима, то имеется нормальный ряд

с циклическими факторами 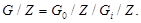 Поскольку в абелевой группе максимальные подгруппы имеют простые индексы, то группа
Поскольку в абелевой группе максимальные подгруппы имеют простые индексы, то группа  обладает рядом
обладает рядом
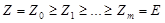
с факторами 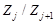 простых порядков. Рассмотрим ряд
простых порядков. Рассмотрим ряд
 <5>
<5>
Так как  , то
, то 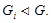 Поскольку все подгруппы из центра группы нормальны в группе, то ряд <5> нормальный. Кроме того, факторы
Поскольку все подгруппы из центра группы нормальны в группе, то ряд <5> нормальный. Кроме того, факторы
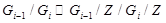
циклические для 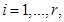 а факторы
а факторы


имеют простые порядки. Значит ряд <5> нормальный с циклическими факторами и группа 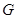 сверхразрешима.
сверхразрешима.
(3) Воспользуемся индукцией по порядку группы. Пусть G - нильпотентная группа и 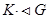 . Тогда K имеет простой порядок. По индукции фактор-группа
. Тогда K имеет простой порядок. По индукции фактор-группа  сверхразрешима. Теперь группа G сверхразрешима по (1).
сверхразрешима. Теперь группа G сверхразрешима по (1).
Лемма 2.3 [1, Лемма 26.3]:
Группа сверхразрешима тогда и только тогда, когда она обладает главным рядом с факторами простых порядков.
Доказательство.
Пусть G сверхразрешима. Тогда она имеет нормальный ряд <1> с циклическими факторами 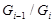 . Так как
. Так как 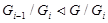 и
и 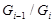 циклическая, то по лемме 1.2, все подгруппы в
циклическая, то по лемме 1.2, все подгруппы в 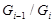 характеристические. Пусть
характеристические. Пусть 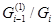 - подгруппа простого индекса в
- подгруппа простого индекса в 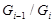 . Тогда
. Тогда

следовательно 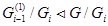 по лемме 1.3, и ряд
по лемме 1.3, и ряд

нормальный с циклическим фактором 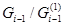 простого порядка. Повторяя эти действия, через конечное число шагов придём к главному ряду с факторами простых порядков.
простого порядка. Повторяя эти действия, через конечное число шагов придём к главному ряду с факторами простых порядков.
Обратно, если группа G имеет главный ряд с факторами простых порядков, то этот ряд будет нормальным, а его факторы циклическими. Значит группа G будет сверхразрешимой.
Теорема 2.1. [1, теорема 26.4]. (1) Максимальные подгруппы сверхразрешимой группы имеют простые индексы
(2) В сверхразрешимой группе каждая минимальная нормальная подгруппа имеет простой порядок.
Доказательство.
(1) Пусть G - сверхразрешимая группа и  . По лемме 2.3 группа G имеет главный ряд
. По лемме 2.3 группа G имеет главный ряд
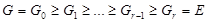 <6>
<6>
с факторами простых порядков. Зафиксируем число i такое что 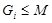 , но
, но 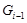

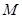 . Поскольку
. Поскольку  и
и 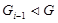 , то
, то 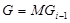 и
и 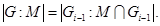
Но 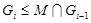 и
и 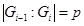 , поэтому либо
, поэтому либо  , либо
, либо 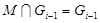 . Поскольку,
. Поскольку, 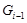
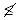
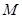 , то
, то  и
и  .
.
(2) Воспользуемся индукцией по порядку группы. Пусть  . По лемме 2.3 в группе G существует минимальная нормальная подгруппа K простого порядка. Если
. По лемме 2.3 в группе G существует минимальная нормальная подгруппа K простого порядка. Если 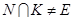 , то N=K и утверждение справедливо. Пусть
, то N=K и утверждение справедливо. Пусть 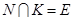 . По лемме 1.4, подгруппа
. По лемме 1.4, подгруппа  - минимальная нормальная подгруппа фактор-группы
- минимальная нормальная подгруппа фактор-группы 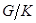 . По индукции
. По индукции  - простое число.
- простое число. 
Лемма 2.4 [1, Лемма 26.5]. Если G - сверхразрешимая группа и p-наибольший простой делитель порядка G, то силовская p-подгруппа группы G нормальна.
Доказательство.
Воспользуемся индукцией по порядку группы G. Пусть  Тогда
Тогда  - простое число теореме 2.1. Фактор-группа
- простое число теореме 2.1. Фактор-группа  сверхразрешима. По индукции,
сверхразрешима. По индукции,  т.е.
т.е. 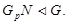 Если
Если 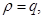 то
то 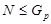 и
и  Пусть
Пусть  тогда
тогда 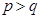 . Так как фактор-группа
. Так как фактор-группа 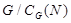 по теореме 1.6, является циклической группой порядка
по теореме 1.6, является циклической группой порядка 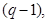 то
то 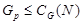 и
и  Но теперь,
Но теперь, 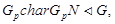 следовательно
следовательно 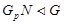 .
. 
Глава 3. Примеры
Заметим, что можно привести пример конечной неабелевой группы, которая является сверхразрешимой.
Пример 3.1. Группа кватернионов Q сверхразрешима, но не абелева.
Пусть Q=<A,B|A4=B4=E, A2=B2, B-1AB=A-1> - группа кватернионов, порожденная матрицами A= 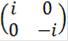 и B=
и B=  .
.
Элементами группы Q являются матрицы:
 ,
, 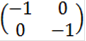 ,
, 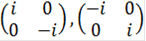 ,
,
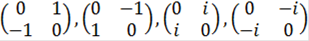 .
.
Таким образом,  =8=23. Следовательно, в силу примера 3.1 группа кватернионов Q сверхразрешима.
=8=23. Следовательно, в силу примера 3.1 группа кватернионов Q сверхразрешима.
Однако группа Q не является абелевой.
Действительно,
A×B= 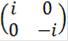 ×
×  =
= 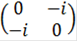 ≠
≠ 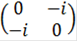 =
=  ×
× 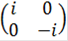 = B×A.
= B×A.
Согласно пункту (3) леммы 2.2. каждая нильпотентная группа сверхразрешима. Обратное утверждение в общем случае не верно. Приведем соответствующий пример.
Пример 3.2. Симметрическая группа S3 степени 3 сверхразрешима, но не нильпотентна.
Пусть S3 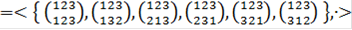 - симметрическая группа степени 3. Найдем все ее собственные подгруппы.
- симметрическая группа степени 3. Найдем все ее собственные подгруппы.
Н1 = < 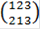 > = <{
> = <{  ,
,  },
}, 
Н2 = < 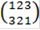 > = <{
> = <{  ,
, 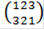 },
}, 
Н3 = <  > = <{
> = <{  ,
,  },
},  ,
,
Н4 = < 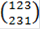 > = <{
> = <{  ,
, 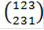 ,
,  },
}, 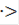 .
.
Подгруппа Н1 не является нормальной подгруппой группы S3. Действительно, выберем 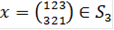 . Пусть
. Пусть 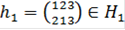 . Тогда
. Тогда  и
и 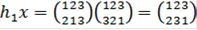 ,
, 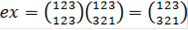 . Следовательно,
. Следовательно, 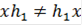 и
и 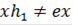 . Таким образом, для
. Таким образом, для 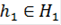 не существует элемента
не существует элемента 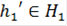 такого, что
такого, что 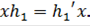 Значит, по определению
Значит, по определению 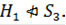
Подгруппа Н2 не является нормальной подгруппой группы S3. Действительно, выберем  . Пусть
. Пусть  . Тогда
. Тогда  и
и 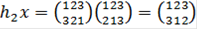 ,
,  . Следовательно,
. Следовательно, 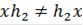 и
и 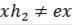 . Таким образом, для
. Таким образом, для  не существует элемента
не существует элемента 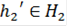 такого, что
такого, что 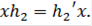 Значит, по определению
Значит, по определению 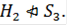
Подгруппа Н3 не является нормальной подгруппой группы S3. Действительно, выберем  . Пусть
. Пусть 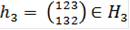 . Тогда
. Тогда 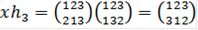 и
и  ,
, 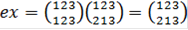 . Следовательно,
. Следовательно,  и
и  . Таким образом, для
. Таким образом, для 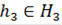 не существует элемента
не существует элемента 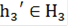 такого, что
такого, что 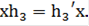 Значит, по определению
Значит, по определению 
Рассмотрим подгруппу Н4. Ее порядок 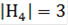 . Следовательно, она является силовской 3-подгруппой группы S3. Поскольку Н4 - единственная силовская 3-подгруппа группы S3, то
. Следовательно, она является силовской 3-подгруппой группы S3. Поскольку Н4 - единственная силовская 3-подгруппа группы S3, то  .
.
Таким образом, группа S3 обладает нормальным рядом 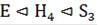 , факторы которого
, факторы которого 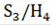 и
и 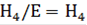 имеют порядки 2 и 3 соответственно, значит, являются циклическими группами. Следовательно, по определению, группа S3 сверхразрешима.
имеют порядки 2 и 3 соответственно, значит, являются циклическими группами. Следовательно, по определению, группа S3 сверхразрешима.
То, что группа S3 не является нильпотентной, следует из того, что она обладает только одной силовской 3-подгруппой 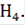
Заключение
В данной курсовой работе были приведены некоторые результаты касающиеся вопроса сверхразрешимости конечных групп, обладающих нормальным рядом с циклическими факторами. Рассмотрены и доказаны некоторые свойства сверхразхрешимых групп в виде лемм во второй главе. В главе три приведены и рассмотрены примеры.
Список используемой литературы
1. Монахов В. С. Введение в теорию конечных групп и их классов. - Гомель: УО «ГГУ им. Ф. Скорины», 2003. - 320 с.;
. Каргаполов М.И., Мерзляков Ю.И. Основы теории групп. - М.: Наука, 1982. - 288 с.;
. Холл М. Теория групп. - М.: Издательство иностранной литературы, 1962. - 468 с.;
. Курош А. Г. Теория групп. - М.: Наука, 1967. - 648 с.;
. Ленг С. Алгебра. - М.: Мир, 1986. - 564 с.