Сферические волны – это волны, для которых волновые поверхности – есть совокупность концентрических колец.
Лучи направлены вдоль радиусов сфер от центра источника волны.
(39)
В случае сферической волны, даже в среде, не поглощающей энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием по закону 
. r – расстояние от центра волны до рассматриваемой точки среды.
Вывод уравнения стоячей волны.
Рассмотрим две волны с одинаковыми амплитудами и частотами, которые распространяются навстречу друг другу:
Уравнение первой волны:
(40)
(41)
При наложении двух волн друг на друга:
(42)
(43)
(44)
| - уравнение стоячей волны |
| - амплитуда стоячей волны |
Координаты узлов и пучностей.
Пучности – точки, в которых амплитуда стоячей волны максимальна 
:
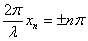
| - координата пучности |
Узлы стоячей волны – точки, в которых амплитуда стоячей волны равна нулю 
:
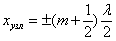
| - координата узлов |
Границы максимальных смещений точек среды в зависимости от их координат изображены на рисунке. Здесь же отмечены координаты х 0,, х 1, х 2,... узлов и координаты х '0, х '1, х '2... пучностей стоячей волны.
Энергия волн.
При распространении волн в среде происходит перенос энергии волной. В это время в среде наблюдаются колебания ее частиц, т.е. частицы среды приобретают 
(за счет движения) и 
(за счет деформации) энергии.
Объемная плотность полной энергии волн равна:
(58)
Если на пути распространения волны поставить некоторую площадку ds, то можно говорить о потоке энергии через эту площадку.
Отношение энергии, переносимой сквозь некоторую площадку к промежутку времени, за который произошел перенос, называют потоком энергии:
(59)
Плотность потока энергии волны (интенсивность звука) 
:
(60)
Вектор плотности потока энергии, :
(62)
| - направление вектора плотности потока энергии совпадает с направлением переноса энергии. |
Уровень интенсивности звука (уровень звуковой мощности) (дБ)
LP=10 1g(I / I 0), (63)
где I 0 — условная интенсивность, соответствующая нулевому уровню интенсивности (I 0=1 пВт/м2).
Уровень громкости звука L N в общем случае является сложной функцией уровня интенсивности и частоты звука и определяется по кривым уровня громкости (рис. 7.1). На графике по горизонтальной оси отложены логарифмы частот звука (сами частоты указаны под соответствующими им логарифмами). На вертикальной оси отложены уровни интенсивности звука в децибелах. Уровни громкости звука отложены по вертикальной оси, соответствующей эталонной частоте v =1000 Гц. Для этой частоты уровень громкости, выраженный в децибелах, равен уровню интенсивности в децибелах. Уровень громкости звуков других частот определяется по кривым громкости, приведенным на графике. Каждая кривая соответствует определенному уровню громкости.
Кривые уровней громкости
Частота, Гц