Лекция 5: Механические волны
План:
1. Длина волны и волновое число.
2. Вывод уравнения плоской бегущей волны.
3. Уравнение плоской бегущей волны в комплексном виде.
4. Разность фаз колебаний.
5. Виды волн.
6. Фазовая и скорость.
7. Групповая скорость.
8. Связь фазовой и групповой скорости.
9. Нахождение групповой скорости методом Эренфеста.
10. Уравнение сферической волны.
11. Вывод уравнения стоячей волны.
12. Координаты узлов и пучностей.
13. Энергия волн.
________________________________________________________________
Длина волны и волновое число
Длиной волны  – называют расстояние между ближайшими точками, колеблющимися в одинаковой фазе.
– называют расстояние между ближайшими точками, колеблющимися в одинаковой фазе.
Формулы длины волны легко получить из аналогии по формуле пути:
 (1)
(1)
 (2)
(2)
 Если период равен
Если период равен  , (3)
, (3)
то  (4)
(4)
Если из (2) выразить период и приравнять его к (3), получим:
 получим
получим  (5)
(5)
Или  (6)
(6)
Физический смысл отношения  заключается в том, что оно показывает сколько длин волн умещается в
заключается в том, что оно показывает сколько длин волн умещается в  единицах длины. Отношение
единицах длины. Отношение  обозначается
обозначается  и называется волновым числом, т.е.
и называется волновым числом, т.е.

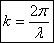
 (7)
(7)

Например:
Вывод уравнения плоской бегущей волны
Бегущие волны – волны, которые переносят в пространстве энергию.
Плоские волны – волны, волновые поверхности которых – есть совокупность параллельных плоскостей, перпендикулярных направлению распространения волны.
Лучи в этом случае – параллельные прямые, совпадающие с направлением скорости распространения волны.
Пусть плоская бегущая волна распространяется вдоль оси X, т.е. вдоль одного направления из точки А в точку В как показано на рисунке:
 Пусть источник колебаний в начальный момент времени
Пусть источник колебаний в начальный момент времени  находится в точке О.
находится в точке О.
Запишем уравнение колебания:
 (8)
(8)
Рассмотрим распространение волны от точки М до точки В. Из рисунка видно, что время  , затраченное на этот путь равно
, затраченное на этот путь равно  , где
, где  - это время, за которое волна распространилась от источника колебаний до точки М.
- это время, за которое волна распространилась от источника колебаний до точки М.
Перейдем от уравнения колебаний к уравнению плоской бегущей волны:
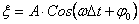 (9)
(9)
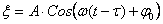 (10)
(10)
Т.к. за время  волна распространилась на расстояние
волна распространилась на расстояние  , тогда
, тогда
 (11)
(11)
 (12)
(12)
 (13)
(13)
Будем считать начальную фазу  .
.
Тогда согласно уравнению (6), получаем:  (14)
(14)
Если в уравнении (14) 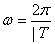 , а
, а  , то получим четвертый вид уравнения плоской бегущей волны (при
, то получим четвертый вид уравнения плоской бегущей волны (при  ):
):

| - первый вид уравнения плоской бегущей волны |

| - второй вид уравнения плоской бегущей волны |

| - третий вид уравнения плоской бегущей волны |

| - четвертый вид уравнения плоской бегущей волны |
 - смещение точек среды с координатой x в момент времени t.
- смещение точек среды с координатой x в момент времени t.
Уравнение плоской бегущей волны в комплексном виде.
Уравнение плоской бегущей волны  можно представить в комплексном виде, используя формулу Эйлера:
можно представить в комплексном виде, используя формулу Эйлера:
 (15)
(15)
Если  , то
, то
 (16)
(16)
Т.к. физический смысл имеет только реальная часть, получаем:
 , (17)
, (17)
Получаем уравнение плоской бегущей волны комплексном виде:
 (18)
(18)

| - уравнения плоской бегущей волны в комплексном виде |
Разность фаз колебаний
Фаза рассчитывается из определения углового перемещения:
 (19)
(19)
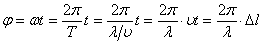 (20)
(20)
 (21)
(21)
Виды волн
Основное свойство всех волн – перенос частицами среды энергии без переноса вещества.
Различают продольные и поперечные волны.
Волны, в которых частицы среды колеблются вдоль их распространения, называются продольными.

Волны, в которых частицы среды колеблются в плоскостях, перпендикулярных к направлению распространения волны, называются поперечными.
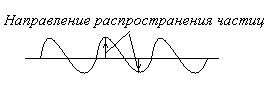
Продольные волны распространяются в жидкостях и газах
В твердой среде возникают как продольные, так и поперечные
Фазовая скорость
Пусть в волновом процессе фаза = const, т.е.
 (22)
(22)
 (23)
(23)
После дифференцирования, получим:
 (24)
(24)
или  (25)
(25)
Вывод: скорость распространения волны есть скорость перемещения фазы волны, поэтому ее называют фазовой скоростью и обозначают: 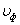 :
:
 Т.к.
Т.к.  , отсюда
, отсюда  (26)
(26)
| Дисперсией называется зависимость фазовой скорости в среде от частоты распространение волн (дисперсия всегда связана с поглощением энергии средой) |
Групповая скорость
Рассмотрим простейшую группу волн, которая получается при наложении двух плоских волн с одинаковыми амплитудами и близкими частотами  и близкими волновыми числами
и близкими волновыми числами  :
:
 (27)
(27)
Это волна отличается от гармонической тем, что ее амплитуда есть медленно изменяющаяся функция координаты от времени, т.е. является негармонической.
 (28)
(28)

| - амплитуда группы волн |
Групповая скорость – скорость распространения группы волн, 
Групповая скорость – скорость максимума огибающей группы волн или скорость движения центра волнового пакета.
Из условия  (29)
(29)
получим:  (30)
(30)
 (31)
(31)
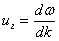
| - групповая скорость |
Связь групповой и фазовой скорости.
Групповая скорость определяется выражением:
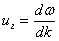 (32)
(32)
Определим отдельно выражения для  и
и  :
:
1)  -?
-?
Из выражения  выразим угловую скорость:
выразим угловую скорость: 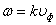 (33)
(33)
Продифференцируем это выражение по k:  (34)
(34)
2)  -?
-?
Выражения  продифференцируем по
продифференцируем по  :
:

или  (35)
(35)
Подставим выражения (34) и (35) в выражение для групповой скорости (32), получим:
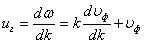 (36)
(36)
 (37)
(37)
 (38)
(38)

| - связь фазовой и групповой скорости |
Из (38) следует, что 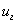 может быть как больше, так и меньше фазовой в зависимости от знака
может быть как больше, так и меньше фазовой в зависимости от знака 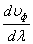 .
.
Если в среде не наблюдается дисперсия волн, то  , тогда фазовая и групповая скорости совпадают
, тогда фазовая и групповая скорости совпадают 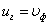 .
.
Понятие групповой скорости очень значимо, т.к. именно она фигурирует при измерении дальности радиолокации, в управлении космическими объектами.
Но  , а для
, а для 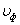 ограничений нет.
ограничений нет.
9. Нахождение групповой скорости методом Эренфеста
 Зависимость групповой скорости от длины волны
Зависимость групповой скорости от длины волны  позволяет определить значение групповой скорости.
позволяет определить значение групповой скорости.
Для этого нужно провести касательную к точке с координатами  и
и  . Можно найти отрезок, отсекаемый касательной на оси ординат, равный значению групповой скорости.
. Можно найти отрезок, отсекаемый касательной на оси ординат, равный значению групповой скорости.