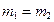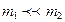Виды энергий в механике.

1) Кинетическая энергия.

Если тело массой m движется со скоростью v, то оно обладает энергией ,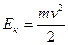

Работа равна изменению кинетической энергии тела: .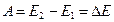

2) Потенциальная энергия.

Любое тело массы m, находящееся под действием гравитации обладает энергией: ,

где h – высота над условным нулевым уровнем, g – ускорение свободного падения.

Потенциальной энергией так же обладает упруго деформированное тело. Если пружина жесткостью k деформирована на величину x, то она обладает энергией: ,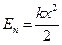

Потенциальная энергия это энергия взаимодействия тел (или его частей).

Отметим, что не всякое взаимодействие тел характеризуется потенциальной энергией. Есть особые силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным положением тел (рис.). Такие силы называют консервативными. Например, к консервативным силам относятся сила тяжести, сила упругости, к неконсервативным – сила трения.

Работа равна изменению потенциальной энергии со знаком минус:

Единица измерения энергии – 1 Джоуль.

Закон сохранения энергии.

Рассмотрим консервативную механическую систему, т.е. такую систему в которой действуют только консервативные силы.

Закон сохранения формулируется для полной энергии.

Полной энергией механической системы называют сумму кинетических и потенциальных энергий тел, входящих в эту систему: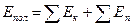

Далее формулируем закон сохранения.

Итак, в замкнутой консервативной механической системе полная энергия сохраняется.

Или, в консервативных системах при отсутствии внешнего воздействия полная энергия остается постоянной.

Часто потенциальная энергия является функцией координат. Изобразим на одной координатной плоскости графики полной энергии и потенциальной энергии. График потенциальной энергии может взрастать или убывать, а график полной энергии горизонтален, т.к. полная энергия постоянна (в консервативных системах).

ABC – потенциальная яма.

CDR – потенциальный барьер.

Центральный удар шаров.

Законы сохранения применяются для анализа и решения множества физических задач, одним из которых является удар тел.

Удар – столкновение двух или более тел, при котором взаимодействие длится очень короткое время.

При ударе между телами происходит перераспределение энергий и импульса. При этом часть механической энергии системы может перейти в немеханические.

Рассмотрим предельные виды удара.

1. Неупругий удар – удар, после которого тела движутся как единое целое, при этом часть механической энергии тратится на деформацию и переходит в немеханические виды (в тепловую). При неупругом ударе выполняется только закон сохранения импульса.
2. Абсолютно упругий удар – удар, при котором механическая энергия не переходит в другие, немеханические, виды энергии. После удара тела полностью восстанавливают формы и размеры. Полная энергия системы сохраняется. При абсолютно упругом ударе выполняются и законы сохранения импульса и энергии.

Рассмотрим центральный удар двух шаров.

Удар называется центральным, если до удара шары движутся вдоль линии, проходящей через их центры масс.

Пусть известны массы m₁, m₂ и скорости шаров до удара: v₁, v₂

Используя законы сохранения импульса и энергии, можно найти скорости шаров после удара: v’₁, v’₂

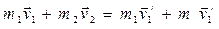
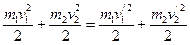
Данная система – это законны сохранения импульса и энергии. Решая данную систему уравнений, находим:

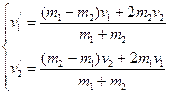
Анализ полученного решения приводит к интересным результатам.

(читателю предлагается самостоятельно получить выводы для приведенных ниже случаев)

P.S.

Есть еще одна сохраняющаяся величина, но её мы рассмотрим в другой лекции.

Конец.