Закон сохранения импульса

Законы сохранения

 

План лекции.

 

1. Импульс тела.

1) 2 закон Ньютона.

2) Закон сохранения импульса.

3) Центр масс.

4) Реактивное движение.

1. Энергия.

1) Работа. Мощность.

2) Механические виды энергий.

3) Закон сохранения энергии.

1. Центральный удар шаров.

 

Импульс тела.

Импульс тела – векторная физическая величина равная произведению массы тела на скорость.

Главным свойством такой величины как импульс является то, что в замкнутых системах тел векторная сумма импульсов всех тел остается постоянной. И совершенно не важно, что происходит в системе - сумма импульсов всегда одна и та же. Такое постоянство формулируется в законе сохранения импульса. Если бы импульс системы не сохранялся, то введение понятия импульса было бы бессмысленным. Отметим, что закон сохранения импульса является фундаментальным законом физики, и пока нет ни одного экспериментального свидетельства опровергающего этот закон. Закон сохранения импульса позволяет быстро и эффективно решать многие задачи, не прибегая к законам Ньютона.

Импульс измеряется в кг*м/с.

 

Второй закон Ньютона.

Запишем 2 закон Ньютона, используя величину импульса:

окончательно — 2 закон Ньютона

Таким образом, 2 закон Ньютона можно сформулировать так: производная импульса тела по времени равна действующей на него силе (сумме сил).

 

Закон сохранения импульса

Закон сохранения импульса можно вывести, используя законы Ньютона, однако он носит самостоятельный характер и не является следствием законов Ньютона.

Покажем, как можно вывести закон сохранения импульса.

Рассмотрим механическую систему из n тел, массы и скорость которых равны m₁,m₂,…m_n и v₁,v₂,…v_n.

_{Для примера изображены три тела. Каждое тело взаимодействует друг с другом. Эти силы назовем внутренними и обозначим синими стрелками. Так же на каждое тело может действовать некая внешняя сила. Внешние силы обозначим красными стрелками. Сумму внутренних сил, действующих на конкретное тело, обозначим F’ , а сумму внешних сил обозначим F . Запишем для каждого тела второй закон Ньютона:}

_{…………..}

 

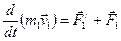
Сложим эти уравнения:

_{По третьему закону Ньютона сила взаимодействия каждой пары тел равны по модулю и противоположны по направлению. Значит, при суммировании внутренних сил они попарно компенсируются и в сумме дадут ноль. Сумма внутренних сил равна нулю, тогда выражение запишется следующим образом:}

В полученном выражении слева от знака равенства стоит изменение суммы _.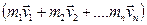

_{Эту сумма представляет собой сумму импульсов всех тел, входящих в механическую систему, и называется импульсом механической системы. Итак, импульс механической системы равен сумме импульсов тел, входящих в систему:}

 

Последнее выражение можно записать так:

_{Но вернемся к выражению . Её можно записать так:}

_, (*)

Если система замкнута, то внешние силы отсутствуют _.

Следовательно

Или

Иначе говоря, импульс замкнутой системы всегда сохраняется.

Теперь можно сформулировать закон сохранения импульса: в замкнутой системе векторная сумма импульсов тел, входящих в данную систему, остается постоянной.

Центр масс.

Центром масс системы материальных точек называется точка С, положение которой в пространстве задается радиус-вектором , определяемым следующим образом

где m_i, r_i - масса и радиус-вектор конкретного тела, а М – масса всей системы тел.

Найдем скорость центра масс:

 

или ,

Таким образом, импульс системы равен произведению массы системы на скорость её центра масс.

Подставив выражение в уравнение (*), получим

В полученном выражении справа от знака равенства стоит сумма внешних сил, действующих на систему. Если система замкнута, то эта сумма равна нулю. Тогда

или

т.е. центр масс движется прямолинейно и равномерно, либо остается неподвижным.

 

Реактивное движение.

Особый интерес представляет реактивный способ передвижения, когда тело отталкивается не от других тел (земля, вода, воздух), а от собственной части. Реактивное движение используется в технике (например, самолеты, ракеты) и в природе. В случае реактивного движения масса тела не остается постоянной, она уменьшается, т.к. часть массы отбрасывается. Что бы описать такое движение 2 закон Ньютона запишется следующим образом:

 

- это выражение называют уравнением Мещерского,

где - скорость истечения газов из ракеты, - внешняя сила.

Пусть внешняя сила равна нулю 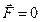, а скорость истечения газов из ракеты постоянна . Тогда

откуда

Полученное выражение называют формулой Циолковского.

 

Энергия.

Энергия, как и импульс, так же обладает свойством сохранения. В замкнутых системах при определенных условиях полная энергия сохраняется. Закон сохранения энергии – важный фундаментальный закон физики. Все явления природы протекают так, что бы энергия сохранялась. В отличие от импульса энергия является скалярной величиной и бывает разных видов: потенциальная, кинетическая, внутренняя, магнитная и т.д. Соответственно и выражения, по которым можно вычислить энергию, так же разные.

Энергия не уничтожается и не появляется из пустоты, она превращается из одного вида в эквивалентный другой вид (например, из механической энергии в электрическую). Закон сохранения энергии иногда называют законом сохранения и превращения энергии.

Выражения, по которым можно вычислить энергию, представляют собой функции состояния системы. Совершая работу энергию можно изменить. Мерой превращения энергии из одного вида в другой является работа. Работа изменяет состояние системы и является функцией процесса. Работа отражает превращение энергии и численно равна изменению энергии.

В дальнейшем будем рассматривать механические виды энергий и механическую работу.

Начнем с понятия работы.

Работа. Мощность.

Механическая работа некоторой силы F есть скалярная величина равная произведению этой силы на перемещение и на угол между направлениями силы и перемещением.

Или, используя векторную алгебру, можем записать так:

Единица измерения работы – 1 Джоуль.

Отметим, что перемещение s необязательно происходит под действием силы F.

В зависимости от угла работа может быть положительной, отрицательной или нулевой.

Если на пути s сила непостоянна, то путь нужно разбит на малые участки ds. На каждом таком участке вычислить так называемую элементарную работу , затем всё сложить. Действия сводятся к интегрированию.

Элементарная работа (работа на малом участке пути) равна:

Работа на всем пути s это интеграл вида:

Вид интеграла определяется зависимостью силы от пути F=f(s). Очень часто такой интеграл не зависит от формы пути, а определяется лишь разностью двух чисел в начале и в конце пути.

Если построить график зависимости силы от пути F=f(s), то работа силы численно равна площади криволинейной трапеции.

Мощностью называют скорость совершения работы. Мощность численно равна работе совершённой в единицу времени. Единица измерения мощности – 1 Ватт.

Математически скорость работы можно написать через производную. Тогда мощность по определению равна:

Если сила постоянна, то путем простых преобразований получим следующее выражение:

Т.е. мощность равна произведению силы на скорость.