Саратовский государственный технический университет
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
С ПОМОЩЬЮ ОБОРОТНОГО МАЯТНИКА
Методические указания
к выполнению лабораторной работы по физике
для студентов всех специальностей
всех форм обучения
Электронное издание локального распространения
Одобрено
редакционно-издательским советом
Саратовского государственного
технического университета
САРАТОВ-2006
Все права на размножение и распространение в любой форме остаются за разработчиком.
Нелегальное копирование и использование данного продукта запрещено.
Составитель – Беляев Илья Викторович.
Под редакцией - Зюрюкина Юрия Анатольевича.
Рецензент – Никишин Евгений Леонардович
410054, Саратов, ул. Политехническая 77,
Научно-техническая библиотека СГТУ,
тел. 52-63-81, 52-56-01
http: // lib.sstu.ru
Регистрационный
Номер 060553Э
© Саратовский государственный
технический университет 2006 г.
Цель работы: определить ускорение свободного падения с помощью оборотного маятника.
Кинематика гармонических колебаний
Основной общей чертой всех колебательных движений является то, что эти движения многократно повторяются или приблизительно повторяются через определенные промежутки времени.
Среди периодических процессов основную и важную роль играют гармонические колебания.
Гармоническими называются колебания, в которых интересующая нас величина x (например, линейное или угловое смещение из положения равновесия) изменяется со временем по закону:
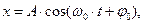(1)
где A – амплитуда (максимальное отклонение от положения равновесия), 
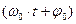- фаза, j0 – начальная фаза, w0 – циклическая (круговая) частота колебаний. Эта частота связана с периодом T (временем одного колебания) и линейной частотой n (числом колебаний за единицу времени) как
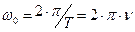. (2)
Продифференцировав (1) по времени, найдем скорость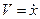 
и ускорение 
:
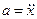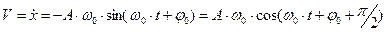, (3)
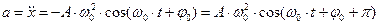. (4)
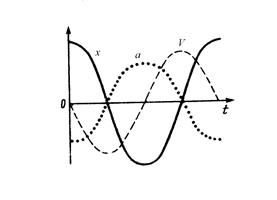Из этих выражений видно, что скорость 
и ускорение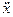 
также изменяются по гармоническому закону. При этом скорость опережает смещение x по фазе на p/2, а ускорение – на p, т.е. находится в противофазе со смещением x. На рисунке приведены графики зависимостей 
, 
, 
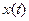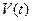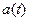для случая 
.
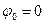Сопоставив (4) и (1), видим, что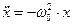 
или
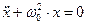(5)
Это дифференциальное уравнение называют уравнением гармонического осциллятора. Его решение (1) содержит две произвольные постоянные: a и
j 0 . Для каждого конкретного колебания они определяются начальными условиями – смещением x0 и скоростью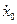 
в начальный момент 
.
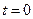Математический маятник
Рассмотрим материальную точку массы m, подвешенную на невесомой нерастяжимой нити длины L и совершающую колебания в вертикальной плоскости. Такой маятник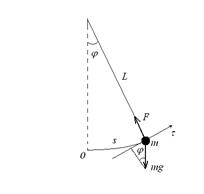 
называется математическим. Запишем второй закон Ньютона в проекции на ось t:
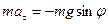. (6)
Учитывая, что угловое ускорение - это вторая производная от угла отклонения по времени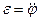 
, а также связь между линейным и
угловым ускорениями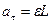 
,
преобразуем (6) к виду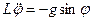 
или
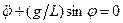. (7)
Из сопоставления этого уравнения с (5) видим, что оно вообще говоря не является уравнением гармонического осциллятора, так как в нем вместо угла отклонения j стоит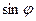 
, однако при малых колебаниях, когда 
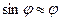, уравнение совпадает с (5):
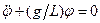. (8)
Откуда следует, что частота w0 и период колебаний T математического маятника, совершающего малые колебания, равны
, 
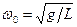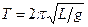. (9)
Физический маятник
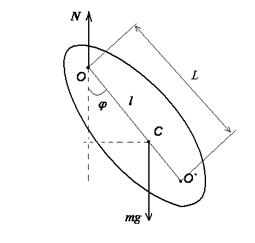Физическим маятником называется твердое тело, совершающее колебания вокруг неподвижной оси, жестко связанной с этим телом. Рассмотрим колебания под действием силы тяжести вокруг горизонтальной оси O, перпендикулярной чертежу. Положение маятника в каждый момент времени можно охарактеризовать углом его отклонения от положения равновесия j. Пусть расстояние от центра масс до оси равно l. Тогда при повороте тела от положения равновесия на угол j возникнет возвращающий момент силы тяжести, равный:
.
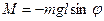Знак минус взят потому, что момент силы тяжести сообщает маятнику ускорение в направлении, обратном отклонению. Момент силы реакции опоры N относительно оси O равен нулю. Уравнение динамики вращательного движения твердого тела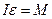 
примет вид
,
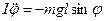где I – момент инерции тела относительно оси O. При малых углах отклонения 
.
Тогда
,
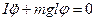или
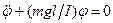. (10)
Колебания будут гармоническими с частотой w0 и периодом T, равными
, 
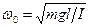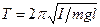. (11)
Такую же частоту и период будет иметь математический маятник длины
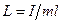, (12)
которую называют приведенной длиной физического маятника.
Точку O`, которая находится на прямой, проходящей через точку подвеса O и центр масс C, и отстоит от точки O на расстоянии L, называют центром качаний физического маятника. Если маятник перевернуть и заставить совершать колебания вокруг оси O`, то период колебаний не изменится. Это можно доказать если использовать теорему Штейнера для момента инерции: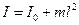 
, и записать выражение (12) так:
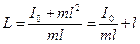, (13)
где I0 – момент инерции относительно оси проходящей через центр масс тела, параллельной оси O. Из (13) следует:
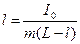; (14)
центр качаний перевернутого маятника согласно (13), будет на расстоянии
.
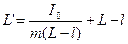Учитывая (14), находим, что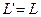 
.
Зная точно приведенную длину L и определяя период колебаний физического маятника, можно измерить величину ускорения свободного падения g. Рабочая формула для определения ускорения свободного падения получается из формулы периода колебаний физического маятника
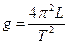. (15)
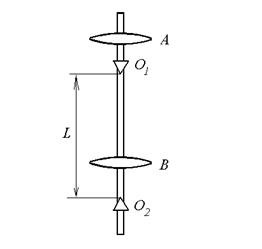
Методика эксперимента
В данной работе используется оборотный маятник, который состоит из стального стержня, на котором жестко закреплены опорные призмы O1 и O2. Ребра опорных призм служат осями качания маятника. На стержне между призмами помещена неподвижная стальная чечевица B. Другая стальная чечевица A находится на одном из концов стержня, ее можно перемещать вдоль стержня, ослабляя фиксирующий винт. На стержне имеется шкала, а на чечевице – нониус, по которому можно отсчитывать положение чечевицы на стержне. Перемещением этой чечевицы добиваются того, чтобы приведенная длина маятника L, была бы равна расстоянию между ребрами призм. Это условие выполняется, если при переворачивании маятника его период колебаний не меняется.
Порядок выполнения работы
1.Устанавливают чечевицу A по нониусу в положении 4,0 см. Отклоняют маятник на 3-4 см от положения равновесия и опускают его. Измеряют время 25 полных колебаний и определяют период с точностью до 0,01с.
2. Не меняя точки опоры маятника, передвигают чечевицу A в положение 6,0 см и снова измеряют период из 25 колебаний.
3. Те же измерения повторяют для положений 8, 10, 12, 14 см.
4. Переворачивают маятник и определяют периоды колебаний при тех положениях чечевицы, что и на первой опоре.
Данные заносят в таблицу.
| Отсчет по шкале, см | ||||||
| T1,с (шкала вверху) | ||||||
| T2,с (шкала внизу) |
5. По полученным данным строят графики зависимости периода колебаний маятника от положения чечевицы.
Точка пересечения графиков указывает положение чечевицы, при котором периоды колебаний на обеих опорах становятся одинаковыми.
6. Устанавливают чечевицу A по нониусу в положение, взятое с графика. В этом положении определяют точное значение периода, измерив время 50 полных колебаний на обеих опорах, с точностью до 0,01с.
7. Подставляют измеренные значения в формулу (15) и вычисляют для каждого значения ускорение свободного падения. Значение приведенной длины L списывают со стенда.
8. Оценивают погрешность результата.
Вопросы для самопроверки
1. Запишите уравнение гармонических колебаний и объясните смысл всех величин входящих в уравнение.
2. Получите уравнение гармонического осциллятора.
3. Выведите формулу периода колебаний математического маятника.
4. Получите выражение для периода колебаний физического маятника.
5. Что такое приведенная длина физического маятника.
6. В чем состоит метод определения ускорения свободного падения с помощью оборотного маятника.
Литература
1. Иродов И.Е. Основные законы механики. М.: Высшая школа, 1997.
2. Савельев И.В. Курс общей физики. Том 1. М.: Наука, любой год издания.
3. Методические указания к оформлению отчетов по лабораторным работам по физике. Изд. Саратовского политехнического института, 1985.