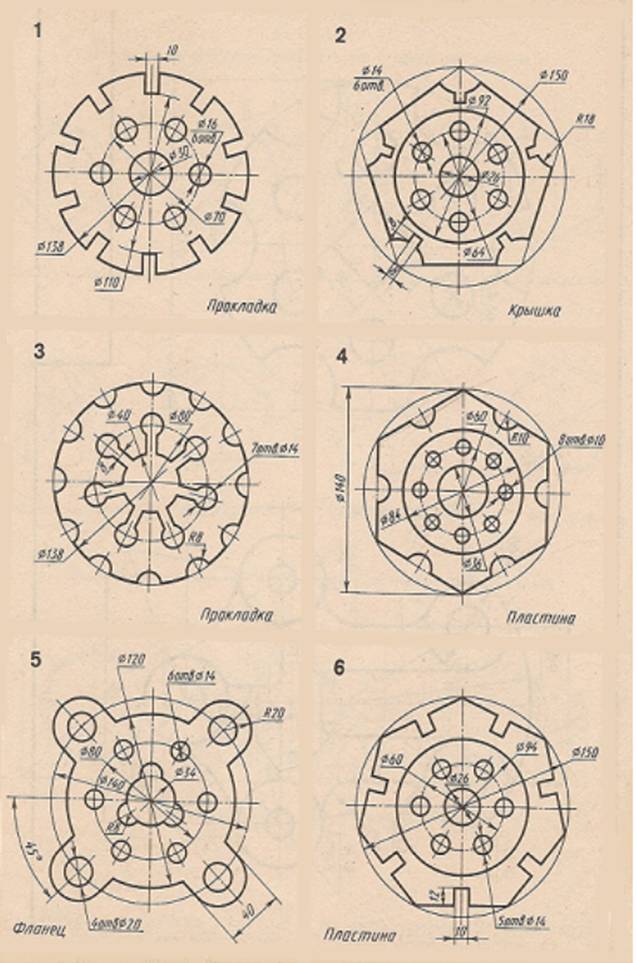
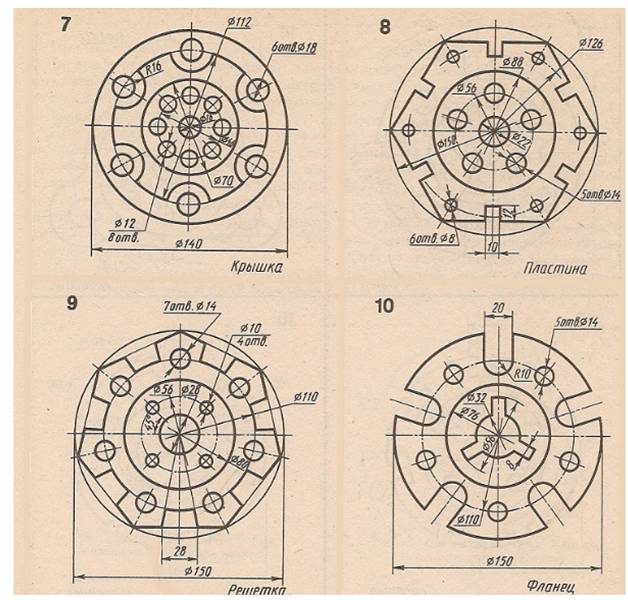
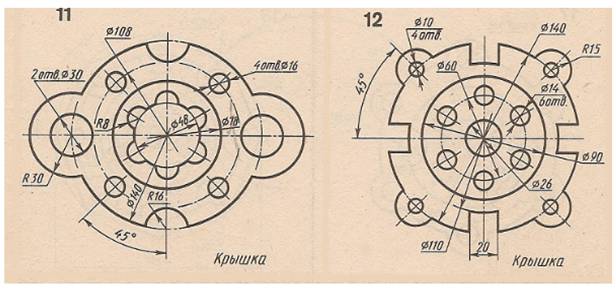
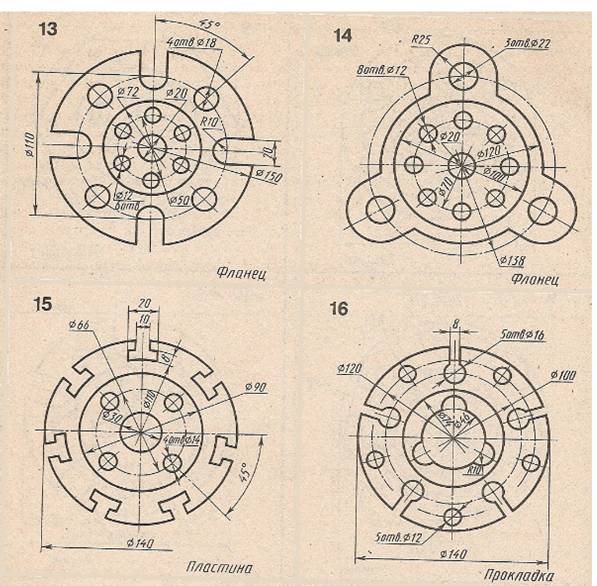
Графическая работа 6. Вычерчивание детали с элементами деление окружности
ЦЕЛЬ РАБОТЫ:
1. Изучить правила деления окружности на равное количество частей.
2. Приобрести навыки вычерчивания детали с применением деления окружности.
ОБОРУДОВАНИЕ И МАТЕРИАЛЫ: Формат А4, чертежные принадлежности.
ОСНОВНЫЕ СВЕДЕНИЯ:
Некоторые детали машин и приборов имеют элементы, равномерно расположенные по окружности. При выполнении таких деталей необходимо знать правила деления окружности на равное количество частей.
Деление окружности на четыре равные части и построение правильного вписанного четырехугольника.
Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части в соответствии с рисунком 1. Соединив точки пересечения этих линий с окружностью прямыми, получим правильный вписанный четырехугольник.
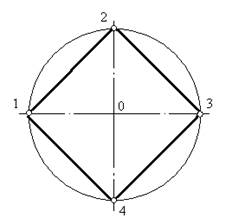
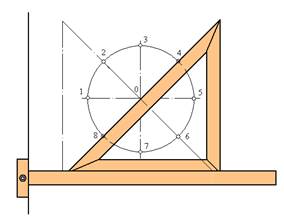
Рисунок 1- Деление Рисунок 2 – Деление на
на четыре части восемь частей
Деление окружности на восемь равных частей и построение правильного вписанного восьмиугольника.
Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым линиям с помощью угольника с углами 45°, 45° и 90° и рейсшины в соответствии с рисунком 2. вместе с центровыми линиями разделять окружность на восемь равных частей.
Деление окружности на восемь равных частей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 в соответствии с рисунком 3. Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.
|
|
Если полученные точки соединить последовательно прямыми линиями, то получится правильный восьмиугольник
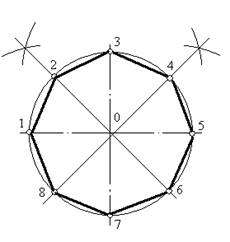
Рисунок 3 - Деление окружности на восемь равных частей
Деление окружности на три равные части и построение правильного вписанного треугольника.
Данные построения выполняют с помощью циркуля или угольника с углами 30°, 60° и 90° и рейсшины.
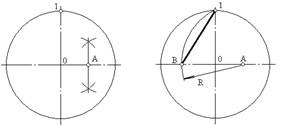
При делении окружности циркулем на три равные части из любой точки окружности, например из точки А пересечения центровых линий с окружностью, в соответствии с рисунком 4, проводят дугу радиусом R, равным радиусу данной окружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на противоположном конце диаметра, проходящего через точку А.
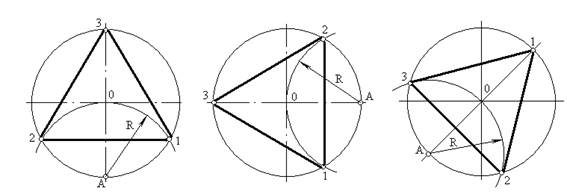
а) б) в)
Рисунок 4 - Деление окружности циркулем на три равные части
Последовательно соединив точки 1, 2 и 3, получим правильный вписанный треугольник. При построении правильного вписанного треугольника, если задана одна из его вершин (например, точка 1), находят точку А. Для этого через заданную точку 1 проводят диаметр, рисунок 4 в). Точка А будет находиться на противоположном конце этого диаметра. Затем проводят дугу радиусом R, равным радиусу данной окружности, и получают точки 2 и 3.
Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника.
Данные построения выполняют с помощью циркуля или угольника с углами 30°, 60° и 90° и рейсшины.
При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5.
|
|
Последовательно соединив полученные точки, получим правильный вписанный шестиугольник в соответствии с рисунком 5
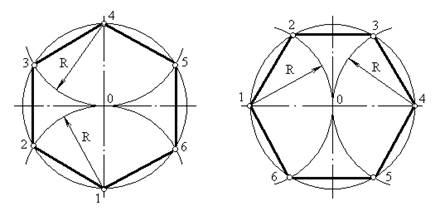
Рисунок 5 - Деление окружности на шесть равных частей
6. Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника.
Данные построения выполняют с помощью циркуля или угольника с углами 30°, 60° и 90° и рейсшины.
При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью в соответствии с рисунком 6, а. Соединив полученные точки, получают правильный вписанный двенадцатиугольник в соответствии с рисунком 6,б.
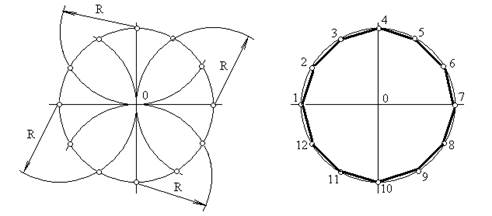
а) б)
Рисунок 6 - Деление окружности на двенадцать равных частей
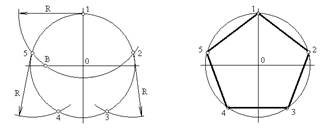
7. Деление окружности на пять и десять равных частей и построение правильных вписанных пятиугольника и десятиугольника.
Половину любого диаметра (радиус) делят пополам, получают точку А в соответствии с рисунком 7,а. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В, в соответствии с рисунком 7,б. Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1/5 длины окружности.
а) б) в) г)
Рисунок 7 - Деление окружности на пять и десять равных частей
Делая засечки на окружности, соответствии с рисунком 7, в, радиусом R, равным отрезку 1В, делят окружность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки 1 строят точки 2 и 5, затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения выполнены правильно в соответствии с рисунком 7,г.
|
|
Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей, но сначала делят окружность на пять частей, начиная построение из точки 1, а затем из точки 6, находящейся на противоположном конце диаметра. В соответствии с рисунком 8,а. Соединив последовательно все точки, получают правильный вписанный десятиугольник в соответствии с рисунком 8,б.
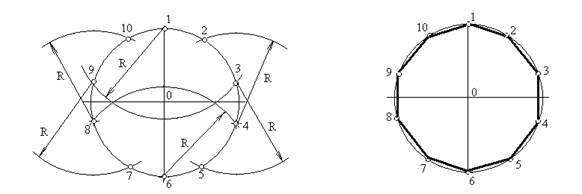
А) б)
Рисунок 8 - Деление окружности на пять и десять равных частей
9. Деление окружности на семь равных частей и построение правильного вписанного семиугольника.
Из любой точки, например точки А, радиусом заданной окружности проводят дугу до пересечения с окружностью в точках В и D в соответствии с рисунком 9,а. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае это отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1/7 длины окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последовательности, в соответствии с рисунком 9,б. Соединив последовательно все точки, получают правильный вписанный семиугольник, рисунок 9,в.
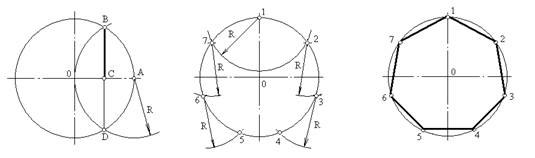
а) б) в)
Рисунок 9 - Деление окружности на семь равных частей
10. Деление окружности на любое число равных частей.
С достаточной точностью можно делить окружность на любое число равных частей, пользуясь таблицей коэффициентов для подсчета длины хорды (таблица 1):
Таблица 1- Коэффициенты для подсчета длины хорды
| Число сторон n | Коэффициент k | Число сторон n | Коэффициент k | Число сторон n | Коэффициент k |
| 0,434 | 0,184 | 0,116 | |||
| 0,383 | 0,174 | 0,112 | |||
| 0,342 | 0,165 | 0,108 | |||
| 0,309 | 0,156 | 0,104 | |||
| 0,282 | 0,149 | 0,101 | |||
| 0,259 | 0,142 | 0,098 | |||
| 0,239 | 0,136 | 0,095 | |||
| 0,223 | 0,130 | 0,092 | |||
| 0,208 | 0,125 | 0,900 | |||
| 0,195 | 0,120 | 0,087 |
Зная, на какое число следует разделить окружность, находят коэффициент k.
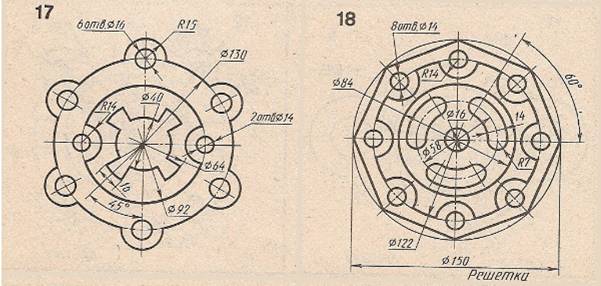
ЗАДАНИЕ:
1.Выполните на формате А4,вертикальнаяориентация.Нанестирамку,основнуюнадпись.
2. По одному из вариантов выполнить контур детали на листе формата А4, применяя правила деления окружности. Нанести размеры. Линии построения не стирать.
ИНДИВИДУАЛЬНОЕЗАДАНИЕ:
номеркарточкисоответствуетпорядковомуномеру студентас1по18;19порядковыйномервыполняет1вариант; 20-2вариант;21-3вариант;22-4вариант;23-5вариант;24-6вариант;25-7вариант;