Линейные диофантовы уравнения
Курсовая работа
Выполнил студент IV курса физико-математического факультета Белов Денис Владимирович
Вятский государственный гуманитарный университет
Киров, 2006 г.
Введение.
Определим цели, стоящие перед данной работой. Для этого дадим два определения.
Определение 1. Диофантовым уравнением 1-ой степени (линейным) с 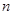 неизвестными называется уравнение вида
неизвестными называется уравнение вида
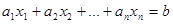 ,
,
где все коэффициенты и неизвестные – целые числа и хотя бы одно  .
.
Для сокращения записи условимся далее сокращать фразу линейное диофантово уравнение, как ЛДУ.
Определение 2. Решением ЛДУ называется упорядоченная n-ка целых чисел 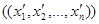 , такая, что
, такая, что 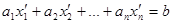 .
.
Нашей целью будет научиться находить решения неопределенного уравнения первой степени, если это решение имеется.
Для этого, необходимо ответить на следующие вопросы:
1). Всегда ли ЛДУ имеет решений, найти условия существования решения.
2). Имеется ли алгоритм, позволяющий отыскать решение ЛДУ.
Работа состоит из двух глав, в первой приведены теоретические материалы, во второй решения некоторых задач.
В части 1.1 приведены выдержки из истории неопределенных уравнений. В части 1.2. в виде теоремы приводится необходимое и достаточное условие существования решения ЛДУ, также говорится о числе решений. Далее рассматриваются методы нахождения решений, в пункте 1.3 для некоторых частных случаев, в пункте 1.4 для любого ЛДУ, имеющего решение.
Диофант и история диофантовых уравнений.
Диофант (Dióphantos) представляет одну из занимательных загадок в истории математики. Мы не знаем, кем был Диофант, точные года его жизни, нам не известны его предшественники, которые работали бы в той же области, что и он. [10]
На могиле Диофанта есть стихотворение-загадка, решая которую нетрудно подсчитать, что Диофант прожил 84 года. О времени жизни Диофанта мы можем судить по работам французского исследователя науки Поля Таннри, и это, вероятно, середина III в.н.э. [10]
Наиболее интересным представляется творчество Диофанта. «Труды его подобны сверкающему огню среди полной непроницаемой тьмы». [Стройк] До нас дошло 7 книг из, возможно, 13 [1], которые были объединены в «Арифметику». Стиль и содержание этих книг резко отличаются от классических античных сочинений по теории чисел и алгебре, образцы которых мы знаем по «Началам» Евклида, леммам из сочинений Архимеда и Аполлония. «Арифметика», несомненно, явилась результатом многочисленных исследований, многие из которых остались нам неизвестны. Мы можем только гадать о её корнях и изумляться богатству и красоте её методов и результатов.
«Арифметика» Диофанта – это сборник задач (их всего 189), каждая из которых снабжена решением и необходимым пояснением. В собрание входят весьма разнообразные задачи, а их решение часто в высшей степени остроумно. Диофант практиковался в нахождении решений неопределенных уравнений вида 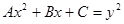 ,
, 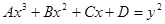 или систем таких уравнений. Типично для Диофанта, что его интересуют только положительные целые и рациональные решения. Иррациональные решения он называет «невозможными» и тщательно подбирает коэффициенты так, чтобы получились искомые положительные, рациональные решения.
или систем таких уравнений. Типично для Диофанта, что его интересуют только положительные целые и рациональные решения. Иррациональные решения он называет «невозможными» и тщательно подбирает коэффициенты так, чтобы получились искомые положительные, рациональные решения.
Поэтому, обычно, произвольное неопределенное уравнение (но, как правило, все-таки с целыми коэффициентами) получает титул "диофантово", если хотят подчеркнуть, что его требуется решить в целых числах.
Неопределенные уравнения 1-й степени начали рассматриваться индусскими математиками позднее, примерно с V века. Некоторые такие уравнения с двумя и тремя неизвестными появились в связи с проблемами, возникшими в астрономии, например, при рассмотрении вопросов, связанных с определением периодического повторения небесных явлений.[2]
Первое общее решение уравнения первой степени 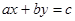 , где
, где  - целые числа, встречается у индийского мудреца Брахмагупты (ок. 625 г). Поэтому, строго говоря, нет оснований называть линейные неопределенные уравнения диофантовыми. Однако, исторически все же сложилось применять термин «диофантово», к любому уравнению, решаемому в целых числах.
- целые числа, встречается у индийского мудреца Брахмагупты (ок. 625 г). Поэтому, строго говоря, нет оснований называть линейные неопределенные уравнения диофантовыми. Однако, исторически все же сложилось применять термин «диофантово», к любому уравнению, решаемому в целых числах.
В 1624 г. в публикуется книга французского математика Баше де Мезирьяка «Problẻmes plaisans et delectables que se font par les nombres». Баше де Мезирьяк для решения уравнения 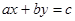 фактически применяет процесс, сводящийся к последовательному вычислению неполных частных и рассмотрению подходящих дробей.
фактически применяет процесс, сводящийся к последовательному вычислению неполных частных и рассмотрению подходящих дробей.
После Баше де Мезирьяка в XVII и XVIII веках различные правила для решения неопределенного уравнения 1-й степени с двумя неизвестными давали Роль, Эйлер, Саундерсон и другие математики.
Цепные дроби к решению таких уравнений были применены Лагранжем, который, однако, замечает, что фактически это тот же способ, который был дан Баше де Мезирьяком и другими математиками, рассматривавшими неопределенные уравнения до него. Неопределенные уравнения 1-й степени стали записываться и решаться в форме сравнения значительно позже, начиная с Гаусса. [2]
В августе 1900 г. в Париже состоялся II Международный конгресс математиков. 8 августа Д.Гильберт прочитал на нем доклад "Математические проблемы". Среди 23 проблем, решение которых (по мнению Д.Гильберта) совершенно необходимо было получить в наступающем XX в., десятую проблему он определил следующим образом:
"Пусть задано диофантово уравнение с произвольным числом неизвестных и рациональными числовыми коэффициентами. Указать способ, при помощи которого возможно после конечного числа операций установить, разрешимо ли это уравнение в целых числах". [7]
Гипотезу, что такого способа нет, первым выдвинул (с достаточным на то основанием) американский математик М.Дэвис в 1949 г. Доказательство этой гипотезы растянулось на 20 лет - последний шаг был сделан только в 1970 г. Юрием Владимировичем Матиясеевичем, на первом году аспирантуры он показал алгоритмическую неразрешимость 10 проблемы Гильберта.
Однако, если про произвольное диофантово уравнения нельзя сказать, имеет ли оно целые корни, или нет, то проблема существования целых корней ЛДУ решена. Приведем теоремы, пользуясь которыми всегда можно сказать, имеет ли целые решения данное ЛДУ или нет.
О числе решений ЛДУ.
Теорема 1. При взаимно простых коэффициентах 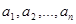 диофантово уравнение
диофантово уравнение

имеет решение в целых числах.
Доказательство. Обозначим через 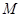 множество тех положительных чисел
множество тех положительных чисел 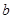 , для которых уравнение
, для которых уравнение

имеет решение в целых числах. 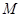 , очевидно, не пусто, так как при заданных
, очевидно, не пусто, так как при заданных  , можно подобрать целые значения
, можно подобрать целые значения  , такие, чтобы
, такие, чтобы 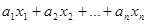 было положительным числом.
было положительным числом.
В множестве 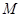 существует наименьшее число (
существует наименьшее число (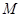 – подмножество натуральных чисел), которое мы обозначим через
– подмножество натуральных чисел), которое мы обозначим через 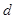
 Обозначим через
Обозначим через 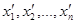 - целые числа, такие, что
- целые числа, такие, что
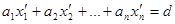 .
.
Пусть 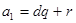 , где
, где  ; тогда
; тогда
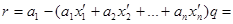
 .
.
Мы подобрали целые значения:  ,
, 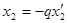 ,…,
,…, 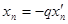 , такие, что
, такие, что  , но
, но  , а
, а 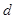 - наименьшее положительное число в
- наименьшее положительное число в 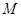 , т. е.
, т. е.  не может быть положительным,
не может быть положительным,  ,
, 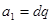 ,
,  .
.
Аналогично получаем:  ,…,
,…, 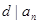 .
.
Мы видим, что 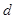 – общий делитель чисел
– общий делитель чисел 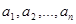 , следовательно, поскольку
, следовательно, поскольку 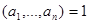 ,
,  ,
, 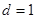 ,
, 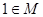 , то уравнение разрешимо в целых числах.
, то уравнение разрешимо в целых числах.
Теорема 2. Пусть 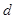 - наибольший общий делитель коэффициентов
- наибольший общий делитель коэффициентов 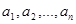 . Диофантово уравнение имеет решение тогда и только тогда, когда
. Диофантово уравнение имеет решение тогда и только тогда, когда 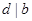 . Число решений такого уравнения равно либо нулю, либо бесконечности.
. Число решений такого уравнения равно либо нулю, либо бесконечности.
Докажем последовательно все три утверждения теоремы.
1). Пусть 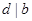 . Для уравнения
. Для уравнения
 ,
,
где 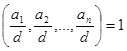 , существуют целые числа:
, существуют целые числа: 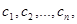 удовлетворяющие ему. Т.е. такие, что
удовлетворяющие ему. Т.е. такие, что
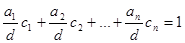 .
.
Тогда
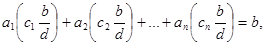
т. е. 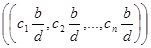 - решение уравнения.
- решение уравнения.
2). Пусть теперь 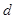 не делит
не делит 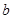 . Тогда левая часть уравнения при любых целых
. Тогда левая часть уравнения при любых целых 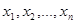 делится на
делится на 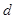 , а правая на
, а правая на 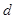 не делиться, так что равенство при целых значениях
не делиться, так что равенство при целых значениях 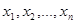 невозможно.
невозможно.
3). Если 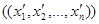 - упорядоченная n-ка чисел, удовлетворяющий уравнению, то например, все n-ки
- упорядоченная n-ка чисел, удовлетворяющий уравнению, то например, все n-ки
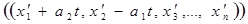 при
при 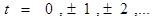
также удовлетворяют этому уравнению и, таким образом, у нас либо совсем не будет решений, либо их будет бесконечное множество.
Если хоть одна пара коэффициентов взаимно простая, то 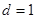 , и уравнение имеет бесчисленное множество решений.
, и уравнение имеет бесчисленное множество решений.