Рассмотрим теперь линейное уравнение с двумя неизвестными
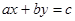 ,
, 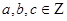 .
.
Покажем несколько алгоритмов для нахождения решения.
Способ 1.
Пусть 
Рассмотрим два случая:
а).  не делится на
не делится на 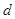 . В этом случае решений нет по теореме 2.
. В этом случае решений нет по теореме 2.
б).  делится на
делится на 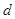 , поделим на
, поделим на 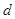 .
.
 ;
;
 .
.
Таким образом получили новое ЛДУ, с тем же множеством решений, но уже со взаимно-простыми коэффициентами. Поэтому далее мы будем рассматривать именно такие уравнения.
Рассмотрим 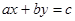 ,
, 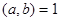 .
.
 , перейдем к сравнению,
, перейдем к сравнению,
 .
.
Т.к. 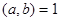 , то сравнение имеет единственное решение
, то сравнение имеет единственное решение  .
.
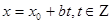 ; подставим в уравнение.
; подставим в уравнение.
 ;
;
 ;
;
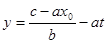 , причем
, причем  .
.
Обозначим  .
.
Тогда общее решение можно найти по формулам: 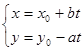 , где
, где  .
.
Пример.  ,
,  .
.
Найдем решение сравнения  ;
;
 ;
;
 , т.е.
, т.е. 

 .
.
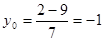 ;
;

Получили общее решение:  , где
, где 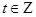 .
.
Способ 2.
Рассмотрим еще один способ нахождения решения ЛДУ с двумя неизвестными, а для этого рассмотрим уравнение вида  . Уравнения такого вида называются линейными однородными диофантовыми уравнениями (ЛОДУ). Выражая неизвестную
. Уравнения такого вида называются линейными однородными диофантовыми уравнениями (ЛОДУ). Выражая неизвестную  , через неизвестную
, через неизвестную  приходим к
приходим к 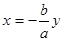 . Так как x должен быть целым числом, то
. Так как x должен быть целым числом, то  , где
, где  - произвольное целое число. Значит
- произвольное целое число. Значит  . Решениями ЛОДУ
. Решениями ЛОДУ  являются n-ки вида
являются n-ки вида 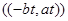 , где
, где  . Множество всех таких n-ок называется общим решением ЛОДУ, любая же конкретная пара из этого множества называется частным решением.
. Множество всех таких n-ок называется общим решением ЛОДУ, любая же конкретная пара из этого множества называется частным решением.
Рассмотрим теперь уравнение  ,
, 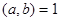 . Пусть n-ка
. Пусть n-ка  его частное решение, а множество n-ок
его частное решение, а множество n-ок  общее решение соответствующего ЛОДУ. Докажем предложение.
общее решение соответствующего ЛОДУ. Докажем предложение.
Общее решение ЛДУ  ,
, 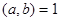 задается уравнениями
задается уравнениями  , где
, где  .
.
Доказательство. То, что правые части указанных в формулировке теоремы равенств действительно являются решениями, проверяется их непосредственной подстановкой в исходное уравнение. Покажем, что любое решение уравнения  имеет именно такой вид, какой указан в формулировке предложения. Пусть
имеет именно такой вид, какой указан в формулировке предложения. Пусть  - какое-нибудь решение уравнения
- какое-нибудь решение уравнения  . Тогда
. Тогда  , но ведь и
, но ведь и  . Вычтем из первого равенства второе и получим:
. Вычтем из первого равенства второе и получим:
 - однородное уравнение. Пишем сразу общее решение:
- однородное уравнение. Пишем сразу общее решение: 
 , откуда получаем:
, откуда получаем:
 . Доказательство завершено.
. Доказательство завершено.
Встает вопрос о нахождении частного решения ЛДУ.
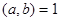
По теореме о линейном разложении НОД, это означает, что найдутся такие  и
и  из множества целых чисел, что
из множества целых чисел, что  , причем эти
, причем эти  и
и  мы легко умеем находить с помощью алгоритма Евклида. Умножим теперь равенство
мы легко умеем находить с помощью алгоритма Евклида. Умножим теперь равенство  на
на  и получим:
и получим:  , т.е.
, т.е.  ,
,  .
.
Таким образом, для нахождения общего решения находим общее решение ЛОДУ, частное решение ЛДУ и их складываем.
Замечание: особенно этот способ удобен, когда  или
или  . Если, например,
. Если, например,  ,
,  , тогда n-ка
, тогда n-ка  , очевидно, будет частным решением ЛДУ. Можно сразу выписывать общее решение.
, очевидно, будет частным решением ЛДУ. Можно сразу выписывать общее решение.
Пример.  ,
, 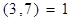 .
.
Найдем частное решение. Используем алгоритм Евклида.
 ;
;
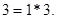
Получаем линейное разложение НОД:
 , т.е
, т.е 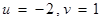 .
.
 ,
, 
Получили общее решение:  , где
, где  .
.
Как видим, получили решение, не совпадающее с решением, найденным первым способом.
Обозначим  и получим
и получим  , т.е эти решения равносильны.
, т.е эти решения равносильны.
Способ 3.
Еще один способ опирается на теорему:
Пусть 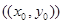 - произвольное решение диофантова уравнения
- произвольное решение диофантова уравнения
 ,
,  , тогда
, тогда
множество решений уравнения в целых числах совпадает с множеством пар  , где
, где  ,
,  , где t – любое целое число.
, где t – любое целое число.
Доказательство этого несложного факта можно найти, например, в книге Бухштаба [2, стр. 114].
Опять же частное решение можно легко отыскать с помощью алгоритма Евклида.
4. Нахождение решений произвольного ЛДУ.
Перейдем теперь к решению ЛДУ с  неизвестных, т. е. уравнений вида
неизвестных, т. е. уравнений вида

где все коэффициенты и неизвестные – целые числа и хотя бы одно  . Для существования решения по теореме 2, необходимо, чтобы
. Для существования решения по теореме 2, необходимо, чтобы 
Положив

перейдем к равносильному уравнению
 (*),
(*),
где 
 . Пусть
. Пусть  ,
, 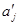 - два ненулевых числа, таких, что
- два ненулевых числа, таких, что 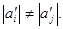 Для определенности предположим, что
Для определенности предположим, что  ,
,  Разделив с остатком
Разделив с остатком  на
на  , получим представление
, получим представление  . Заменив
. Заменив  на
на  в уравнении (*), приведем его к виду
в уравнении (*), приведем его к виду

Перепишем это уравнение в виде
 (**)
(**)
где
 ,
,  .
.
Очевидно, что решения уравнения (*) и (**) связаны между собой взаимно однозначным соответствием и, таким образом, решив уравнение (**), несложно найти все решения уравнения (*). С другой стороны отметим, что


Отметим также, что

Следовательно, за конечное число шагов уравнение (*) приведется к виду
 (***)
(***)
где числа 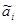 (i = 1,...,n), которые не равны нулю, равны между собой по абсолютной величине. Из соотношения
(i = 1,...,n), которые не равны нулю, равны между собой по абсолютной величине. Из соотношения  следует, что числа
следует, что числа 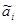 могут принимать только значения 0,±1, причем не все из них равны нулю. Предположим, для определенности,
могут принимать только значения 0,±1, причем не все из них равны нулю. Предположим, для определенности, 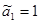 . Тогда уравнение (***) имеет следующее решение:
. Тогда уравнение (***) имеет следующее решение:

где t2, t3,..., tn - произвольные целые числа. Отсюда, учитывая проведенные замены, получается и решение уравнения (*). Отметим, что при получении решения уравнения (***) использовался лишь факт, что  , поэтому, при выполнении алгоритма можно остановиться на том шаге, когда хотя бы один из коэффициентов станет равным ±1.
, поэтому, при выполнении алгоритма можно остановиться на том шаге, когда хотя бы один из коэффициентов станет равным ±1.
5. Примеры решений задач.
1). Решить в целых числах уравнение
4x - 6y + 11z = 7, (4,6,11)=1.
Разделив с остатком -6 на 4, получим -6 = 4(-2) + 2. Представим исходное уравнение в виде
4(x - 2y) + 2y + 11z = 7.
После замены x = x - 2y это уравнение запишется следующим образом
4x + 2y + 11z = 7.
Учитывая, что 11 = 2·5 + 1, преобразуем последнее уравнение:
4x + 2(y + 5z) + z = 7.
Положив y = y + 5z, получим
4x + 2y + z = 7.
Это уравнение имеет следующее решение: x, y - произвольные целые числа, z = 7 - 4x - 2y.
Следовательно y = y - 5z = 20x + 11y - 35, x = x + 2y = 41x + 22y - 70.
Таким образом, решение исходного уравнения имеет вид
 , где
, где  ,
,  - произвольные целые числа.
- произвольные целые числа.
2). Решить в целых числах уравнение

Разделим 5 на -4 с «остатком»,  , преобразуем исходное уравнение к виду
, преобразуем исходное уравнение к виду
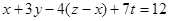 .
.
Заменив  получим
получим  , следовательно
, следовательно
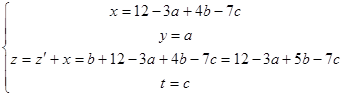 , является решением данного ЛДУ.
, является решением данного ЛДУ.
Список литературы
Башмакова, И.Г. Диофант и диофантовы уравнения [Текст]. – М.: «Наука», 1972 г. - 68 с.
Бухштаб, А. А. Теория чисел [Текст]. - М.: Государственное учебно-педагогическое издательство министерства просвещения РСФСР, 1960. - 378 с.
Виноградов, И.М. Основы теории чисел: Учебное пособие. 11-е изд. [Текст]. – СПб.: Издательство «Лань», 2006. - 176 с.
Гаусс, Карл Фридрих Труды по теории чисел. Под общей ред. Виноградова И.М. [Текст] – М.: Изд. академических наук СССР, 1959 г. - 980 с.
Гельфонд, А.О. Решение уравнений в целых числах. Популярные лекции по математике, вып. [Текст]. М.: «Гостехиздат», 1957 г. - 66 с.
Давенпорт, Г. Введение в теорию чисел [Текст]: Пер. с английского Мороза Б.З. под ред. Линника Ю.В. – М.: «Наука», 1965 г. - 176 с.
Матисеевич, Ю.В. Десятая проблема Гильберта [Текст]. - М.: «Физматлит», 1973 г. - 224 с.
Михелович, Ш.Х. Теория чисел [Текст]. – М.: «Высшая школа», 1962 г. - 260 с.
Соловьев, Ю. Неопределенные уравнения первой степени [Текст]: Квант, 1992 г., №4.
Стройк, Д.Я. Краткий очерк истории математики [Текст]. – М.: «Наука», 1990 г. - 256 с.
Для подготовки данной работы были использованы материалы с сайта https://revolution.allbest.ru/