Федеральное государственное бюджетное образовательное
Учреждение высшего профессионального образования
«Кузбасский государственный технический университет
Имени Т.Ф. Горбачева»
Т. М. Черникова, М. М. Еремеев
ЭЛЕКТРОСНАБЖЕНИЕ С ОСНОВАМИ ЭЛЕКТРОТЕХНИКИ
Методические указания для самостоятельных работ
Рекомендовано учебно-методической комиссией направления 270800.62 «Строительство» в качестве электронного издания
для использования в учебном процессе
Кемерово 2013
Рецензенты:
Т. М. Черникова – доцент кафедры общей электротехники;
Угляница А.В., проф., председатель УМК направления подготовки 270800 «Строительство»
Черникова Татьяна Макаровна, Еремеев Михаил Михайлович.
Электроснабжение с основами электротехники - методические указания для самостоятельных работ [Электронный ресурс] для студентов направления подготовки 270800.62 «Строительство» профилей 270801.62 «Промышленное и гражданское строительство», 270809.62 «Экспертиза и управление недвижимостью», 270815.62 «Автомобильные дороги», 270804.62 «Водоснабжение и водоотведение» всех форм обучения / Т. М. Черникова, М. М. Еремеев. – Электрон. дан. - Кемерово: КузГТУ, 2013. – 30 с.- 1 электр. опт. диск (CD-ROM); 12 см. – Сист.-требования: Pentium 4, Windows 2003, (CD-ROM -дисковод); - Загл. с экрана.
.
Содержит основные теоретические положения, необходимые для расчета цепей постоянного тока, цепей синусоидального тока, трехфазных
цепей, варианты заданий, вопросы к коллоквиумам и список необходимой литературы.
Ó КузГТУ
Ó Черникова Т.М.
Ó Еремеев М.М.
СОДЕРЖАНИЕ
Введение 4
Задание №1. Цепи постоянного тока 5
Вопросы к заданию №1 14
Задание №2. Однофазные цепи переменного тока 15
Вопросы к заданию № 22
Задание №3. Трехфазные цепи переменного тока 23
Вопросы к заданию № 3 27
Приложение I 28
Приложение II 29
Вопросы для зачета 30
Список рекомендуемой литературы 32
ВВЕДЕНИЕ
Дисциплина "Электроснабжение с основами электротехники" состоит из лекционных, практических занятий. При наличии практических занятий предусмотрено выполнение студентами самостоятельной работы с целью лучшего усвоения теоретических знаний и получение навыков расчета задач, с которыми будущие специалисты могут встретиться в своей практической деятельности.
Методические указания к самостоятельной работе содержат три задания и вопросы к заданиям, охватывающие основные разделы теоретического курса: цепи постоянного тока, цепи однофазного и трехфазного переменного тока. Каждое задание имеет 999 вариантов и для исключения дублирования задается трехзначным шифром. Задание составлено так, что преподаватель по своему усмотрению может как упростить его, так и усложнить. Указания рассчитаны на студентов, уже проработавших соответствующие разделы курса.
Отчет по заданиям оформляется на листах формата А4 или на развернутых тетрадных листах. На титульном листе указываются: название вуза, кафедры, наименование задания, номер варианта, учебная группа, Ф.И.О. автора и проверяющего преподавателя. Графические материалы должны выполняться в соответствии с типовыми требованиями. Сроки сдачи самостоятельных работ – 2-я, 3-я и 4-я контрольная неделя соответственно для 1-го, 2-го и 3-го задания.
ЗАДАНИЕ № 1
Электрические цепи постоянного тока
Цель задания - научиться самостоятельно рассчитывать сложные электрические цепи постоянного тока с несколькими источниками энергии и освоить основные методы расчета.
Задание.
1.лПредварительно преобразовав пассивный треугольник в эквивалентную звезду, рассчитать токи во всех ветвях схемы методом узловых потенциалов.
2. Рассчитать токи в исходной схеме методом контурных токов.
3. Методом эквивалентного генератора определить ток в Nк-ой ветви.
4. Составить баланс мощностей.
5.лПостроить потенциальную диаграмму для контура, содержащего две ЭДС.
Исходные данные в табл. 1.1, схема - в прил. I.
Таблица 1.1
| N п/п | Nk | Е1 | E2 | R1 | R2 | R3 | R4 | R5 | R6 |
| Схема | № ветви | В | В | Ом | Ом | Ом | Ом | Ом | Ом |
| 1 цифра | 2 цифра | 3 цифра |
Домашнее задание задается трехзначным шифром. По первой цифре шифра задается схема и ветвь, в которой нужно определить ток методом эквивалентного генератора. По второй цифре задаются значения ЭДС и по третьей - значения сопротивлений.
Пример расчета задания №1
1.1. Преобразование пассивного треугольника
в эквивалентную звезду
Рассмотрим схему на рис. 1.1.
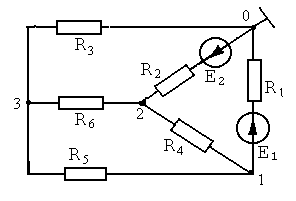
|
Рис. 1.1
В данной схеме (рис. 1.1) пассивным является треугольник, содержащий сопротивления R4, R5, R6.
Упрощаем схему путем преобразования пассивного треугольника в эквивалентную звезду (рис. 1.2).
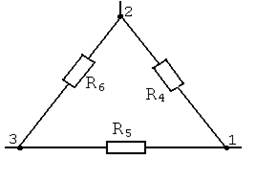
|
 |
 2
2
 |
R46





 R56 01 R45
R56 01 R45


 3 1
3 1
Рис. 1.2
R45=R4R5/(R4+R5+R6);
R46= R4R6/(R4+R5+R6 );
R56=R5R6/(R4+R5+R6 ).
В результате преобразования получим схему с двумя узлами
(рис. 1.3):
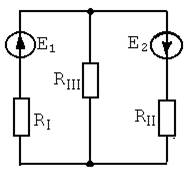
|
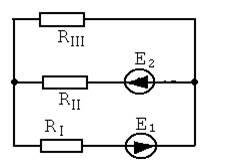
|
RI = R1+R45,
RII = R2+R46,
RIII = R3+R56.
a б
Рис. 1.3
1.2. Расчет методом наложения
Для расчета используем упрощенную схему с двумя узлами
(рис. 1.4, а).
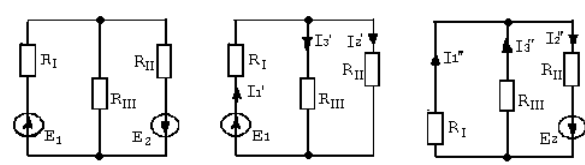
|
а б в
Рис. 1.4
Расчет проводим в последовательности:
а) исключаем из схемы Е2 (рис. 1.4, б). Задаем направление токов I1¢, I2¢, I3¢;
б) методом свертывания схемы определяем токи, создаваемые E1 (I1¢; I2¢; I3¢):
I1¢ = E1 / Rэкв, Rэкв = RI +RIIRIII / (RII + RIII),
I2¢ = I1RIII / (RI + RIII), I3¢ = I1RII / (RII + RIII);
в) делаем проверку по первому закону Кирхгофа;
г) исключаем ЭДС Е1 (рис. 1.4, в). Задаем направления токов I1¢¢, I2¢¢, I3¢¢;
д) аналогично п. б) определяем токи I1¢¢; I2¢¢; I3¢¢. Делаем проверку по первому закону Кирхгофа;
е) определяем токи в упрощенной схеме (рис. 1.4, а) как алгебраическую сумму токов, найденных в п. б) и д). Знак (+) ставим перед частичным током, если его направление совпадает с направлением этого тока в исходной схеме;
ж) делаем проверку по первому закону Кирхгофа.
1.3. Метод двух узлов
(частный случай метода узловых потенциалов)
Расчет проводим в последовательности:
а) задаем направление токов и напряжение в ветвях преобразованной схемы. Для схемы рис. 1.5 определяем проводимость ветвей:
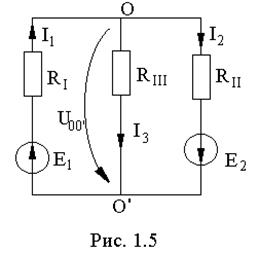
|
g1 = 1 / RI ,
g2 = 1 / RII ,
g3 = 1 / RIII;
б) определяем узловое напряжение, используя метод двух узлов.
Для схемы рис. 1.5:
U00¢ = 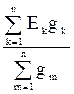 ; U00¢ =
; U00¢ = 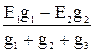 ,
,
где знак (±) зависит от взаимного направления E1 и E2: если ЭДС направлена к узлу 0 - (+), если от узла 0 - (-).
в) определяем токи в ветвях упрощенной схемы по закону Ома для активного участка цепи:
I1 = (E1 - U00¢) / RI I2 = (E2 + U00¢) / RII I3 = U00¢ / RIII;
г) делаем проверку по первому закону Кирхгофа;
д) находим остальные токи в исходной непреобразованной схеме с помощью уравнений второго и первого законов Кирхгофа. Причем, если у полученных значений тока или напряжения окажется знак (-), то это означает, что их действительное направление противоположно выбранному;
е) делаем проверку расчетов по первому закону Кирхгофа для любых двух узлов, используя исходную схему и расчетные значения токов.
1.4. Расчет методом контурных токов
Расчет проводится в последовательности:
а) выбрать направление контурных токов и положительные направления токов во всех ветвях (рис. 1.6);
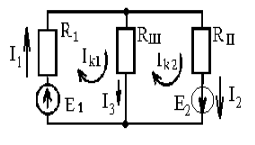
Рис. 1.6
б) составить систему двух уравнений:
Ik1R11 - Ik2R12 = E11,
- Ik1R12 + Ik2R22 = E22 ;
где R12 = R21 - взаимные сопротивления контуров; R11, R22 - собственные сопротивления контуров, равные сумме сопротивлений соответствующего контура; E11 , E22 - сумма ЭДС соответствующего контура.
Знак взаимного сопротивления определяется направлением контурных токов в нем. Если контурные токи во взаимном сопротивлении совпадают по направлению, то R12 берется со знаком (+), если нет, то (-).
Для схемы рис. 1.6 уравнения имеют вид:
Ik1(RI + RIII) - Ik2RIII = E1,
- Ik1RIII + Ik2(RIII + RII) = E2.
Если направление ЭДС совпадает с направлением контурного тока, ставится знак (+), если не совпадает, то (-).
Решение системы уравнений с помощью определителей:
| D1 = |
| D = |


 RI + RIII - RIII E1 - RIII
RI + RIII - RIII E1 - RIII
- RIII RIII + RII; E2 RIII + RII;
| D2 = |

 RI + RIII E1
RI + RIII E1
- RIII E2.
Токи во внешних ветвях равны соответствующим контурным токам, а в смежных - алгебраической сумме соответствующих контурных токов.
Ik1 = I1 = D1 / D, Ik2 = I2 = D2 / D.
Для схемы рис. 1.6 I3 = Ik1 - Ik2, т.к. контурные токи в резисторе RIII направлены навстречу друг другу;
в) делаем проверку по первому закону Кирхгофа;
г) сравниваем токи, найденные методом контурных токов, с токами, найденными другими методами. Они должны быть равны.
1.5. ОПРЕДЕЛЕНИЕ ТОКОВ В ЭКВИВАЛЕНТНОМ ТРЕУГОЛЬНИКЕ ИСХОДНОЙ СХЕМЫ
С ИСПОЛЬЗОВАНИЕМ УРАВНЕНИЙ ВТОРОГО ЗАКОНА КИРХГОФА
|
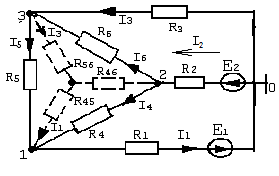 |
Рис. 1.7
Для схемы рис. 1.7 уравнения второго закона Кирхгофа имеют вид (направление обхода контуров – по часовой стрелке):
E2 = I2R2 + I6R6 - I3R3;
-E2 - E1 = - I2R2 - I1R1 - I4R4;
0 = I4R4 + I5R5 - I6R6.
Отсюда получаем:
 ;
;
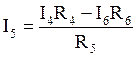 ;
;
 .
.
Если в результате решения этих уравнений ток получится со знаком (-), то это означает, что действительное направление тока противоположно выбранному.
1.6. определение тока IK (к = 5) Методом эквивалентного генератора
Определяем ЭДС эквивалентного генератора Еэкв, то есть напряжение между узлами, к которым подключена nk(к=5) ветвь. Для этого убираем ветвь с R5 (рис. 1.8) и находим токи в оставшейся схеме любым ранее рассмотренным методом.
Например, в схеме на рис. 1.8 находим токи методом двух узлов.
U02 = [(E1(R1+ R4)) - (E2/R2)] / [(1/(R1+ R4))+(l/ R2)+(l/(R3+ R6)).

|
Рис. 1.8
I1 = (E1-U02) / (R1+R4); I2 = (E2 + U02) / R2;
I3 = U02 / (R3 + R6).
Определяем Еэкв = Uxx = j1 - j3 ,
где j0 = 0; j3= - I3 R3 ; j1 = I1R1 - E1.
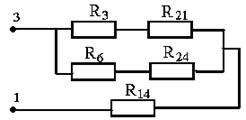
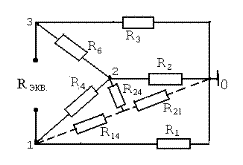
Для того чтобы найти внутреннее сопротивление эквивалентного генератора относительно зажимов (3) и (1), закорачиваем все ЭДС и рассчитываем схему методом эквивалентных преобразований
(рис. 1.9).
|
|
а б
Рис. 1.9
R21 = R2 R1/(R1+ R2+ R4),
R14 = R4R1/(R1+ R2+ R4),
R24 = R2R4/(R1+ R2+ R4),
Rэкв = R14+[(R3+R21)(R6+R24)/(R3+R21+R6+R24)].
Находим ток в пятой ветви: I5 = Eэкв / (Rэкв + R5).
Значение тока Ik (I5) должно соответствовать значению тока в этой ветви, найденному другими методами. Значения токов, вычисленные разными методами, запишем в табл. 1.2. Погрешность расчета не должна превышать 2 %.
Таблица 1.2
| Метод расчета | I1 | I2 | I3 | I4 | I5 | I6 |
| Наложения | ||||||
| Узлового напряжения | ||||||
| Контурных токов | ||||||
| Эквивалентного генератора |
1.7. Баланс мощностей
По закону сохранения энергии мощность, потребляемая от источника, равна мощности, выделяемой в потребителе:
± E1I1 ± E2I2 = I12 R1 + I22 R2 + I32 R3 + I42 R4 + I52 R5 + I62 R6 .
Знак перед произведением E и I определяется по направлению
E и I: если они совпадают, берется (+), если противоположны - (-). Погрешность расчета баланса мощностей не должна превышать 2 %.
1.8. Построение потенциальной диаграммы
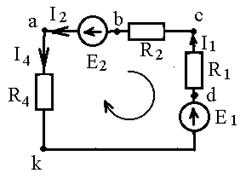
Для построения потенциальной диаграммы выбираем любой контур исходной схемы, содержащей две ЭДС (E1 и E2). Обозначим истинные направления токов в ветвях и зададим направление обхода контура, заземлим любую точку контура и вычислим потенциалы всех других точек (см. пример расчета рис. 1.10). Потенциальная диаграмма приведена на рис. 1.11.
|
ja = 0;
jb= ja - E2;
jc= jb+ I2 R2;
jd = jc + I1R1;
jk = jd - E1;
ja = jk + I4R4 = 0.
Рис. 1.10


 j,(В) d
j,(В) d

 c
c
a R(Oм)


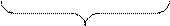


 а
а
R2 R1 R4
 b
b
-j
Рис. 1.11
ВОПРОСЫК ЗАДАНИЮ № 1
Цепи постоянного тока. Алгоритмы расчета цепей с последовательным, параллельным и смешанным соединением сопротивлений.
ЗАДАНИЕ № 2
